航空发动机部件老化对涡轮性能的影响研究

Study of the Effect of Engine Component Deterioration on Turbine Performance

摘要: 本文主要针对压气机和涡轮核心部件性能衰退开展研究。考虑三种情况：压气机性能老化，涡轮性能老化，压气机和涡轮部件性能同时老化，将部件性能老化模型插入到发动机稳态计算模型中修正部件特性，得到对应的涡轮部件性能变化。基于流场仿真技术建立匹配的涡轮部件模型，依据性能衰退模型修改涡轮进出口边界条件和转速，得到涡轮气流流场和压力场分布，进一步分析了性能衰退前后的涡轮性能。所得结论对单个部件乃至整机性能衰退以及各部件之间的相互影响具有一定参考价值。

Abstract: This paper focuses on the performance degradation of compressor and turbine core components. Considering three conditions: performance deterioration of compressor, turbine, compressor and turbine, embedding component performance deterioration model into stable engine computation model and modifying component characteristic, change of turbine component was analyzed. The matching turbine component model was established based on floating field simulating technology, the turbine floating field and the pressure field were calculated by modifying inlet and outlet boundary condition and rotor speed based on deterioration model, and the total performance was analyzed around performance deterioration. The results offer theoretical reference to single component even engine performance deterioration and effect between components.

1. 引言

国外已有相关文献开展对发动机性能衰退的研究 [1] [2] ，国内则开展的较晚 [3] [4] [5] 。通常的研究思路将发动机作为一个整体，任一部件性能的改变都会影响其它部件的性能。西北工业大学的王占学教授利用某型涡扇发动机设计模型，建立性能衰退的模型，研究了整机性能老化的情况 [6] 。文献 [7] 利用涡轮叶型数据，建立涡轮实体模型，基于等价雷诺数修正原理，通过流场仿真技术，定量研究了涡轮叶片由于积垢沉淀等因素引起的叶片粗糙度增大，从而导致其性能衰退的程度。

国内的研究主要围绕着涡轮部件的叶型气动性能和低雷诺数条件下涡轮性能进行研究，并对定常和非定常流动下涡轮性能进行数值模拟。针对使用过程中单个部件老化对发动机部件甚至整机的性能影响研究得较少。除了涡轮自身部件老化问题以外，其他部件性能老化也会对其性能产生影响。当单个部件出现老化时，由于各部件的共同工作必然会影响到其它部件的性能。

本文主要针对压气机和涡轮核心部件性能衰退开展研究。主要研究了单个压气机部件、涡轮部件自身老化出现性能衰退以及两个部件的性能同时出现衰退时，对涡轮部件的性能影响。所得结论对部件乃至整机性能衰退以及航空发动机的控制调节有一定的参考价值。

2. 部件老化计算模型

本文以效率和流量损失衡量部件损失。定义的部件效率和流量失效因子如下：

$eta1=\left({\eta }^{\prime }-{\eta }_0\right)/{\eta }_0$ (1)

$eta2=\left(m^{\prime }-m_0\right)/m_0$ (2)

其中， $eta1$ 为部件效率失效因子， $eta2$ 为部件流量失效因子， ${\eta }_0$ 为稳定状态性能未衰退时的效率， $\eta$ 为其性能衰退的效率。 $m_0$ 为稳定状态性能未衰退时的流量， $m^{\prime }$ 为其性能衰退的流量。计算流程及原理如图1所示。

由图1可知，单个部件性能老化(压气机和涡轮部件)对发动机性能衰退的影响，涉及到所有发动机核心部件。按照气路部件顺序，基于部件匹配技术，通过保持发动机部件间的动量守恒、流量连续和能量守恒，建立描述发动机工作的非线性方程组 [6] 。将部件失效模型(图1中压气机和涡轮部件的老化系数)插入到发动机稳态模型中，通过修改失效部件的特性参数完成性能衰退的计算。首先确定六个初始参数，迭代求解非线性方程组使其收敛，直到使所有共同方程的误差平方和都小于某一误差限制(这里取0.06)或者达到规定的循环次数(取20)的对应一组数据，即为发动机的平衡工作点。采用N-R法求解发动机稳态模型(寻找共同工作点)。

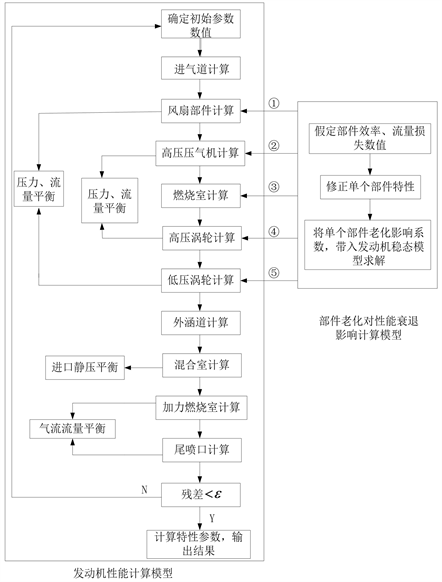
Figure 1. Computation flow chart of effect of component deterioration on engine performance

图1. 考虑部件老化对发动机性能衰退影响的计算流程

考虑部件老化对发动机性能衰退的计算模型，对风扇、高压压气机、燃烧室、高、低压涡轮等部件的特性进行修正，用修正后的部件特性参数重新计算发动机的平衡工作点。在此基础上，定量研究部件性能老化对涡轮性能的影响。

考虑三种代表性情况，研究发动机单个部件老化对涡轮性能的影响。情况1：压气机部件老化对涡轮性能的影响；情况2：整机中涡轮部件老化对涡轮性能的影响；情况3：压气机和涡轮部件同时老化对涡轮性能的影响。同时约定：将性能参数(效率和流量)损失1%的情况记为小幅衰退，性能参数损失2%的情况记为大幅衰退。

3. 建立流场仿真模型

利用流场仿真技术研究涡轮的性能衰退。首先建立涡轮部件模型，比较涡轮在正常状态下，不同转速性能参数计算数值与设计数值，检验所建涡轮模型的精度。计算发现，在不同转速下，效率和落压比的最大相对误差为1.59%和1.95%，在允许的误差范围内。因此所建模型有效。

4. 老化模型与流场仿真混合求解

针对前述三种代表性情况，利用部件衰退模型修改部件特性，将失效因子带入到发动机稳态模型中去，得到三种情况涡轮进出口特性参数的相对变化。利用建立的匹配的涡轮模型，依据衰退模型修改对应的进出口边界条件和转速，进一步分析涡轮流场的特性。其中，进口指定不同径向高度上的总温和总压，出口指定不同半径的静压。分析涡轮叶片表面气流流场以及总压分布，以及沿叶片50%截面弦长的总压分布。

以某涡轮为研究对象，湍流模型采用“Spalart-Allmaras”模型。其中，连续方程为：

$\frac{\partial \left(\rho u_i\right)}{\partial x_i}=0$ (3)

动量方程即雷诺平均的“Navier-Stockes (N-S)”方程：

$\frac{\partial \left(\rho u_j{u}_i\right)}{\partial x_j}=-\frac{\partial p}{\partial x_j}+\frac{\partial \left[{\mu }_e\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]}{\partial x_j}$ (4)

“Spalart-Allmaras (S-A)”湍流模型方程如下：

$\frac{\partial }{\partial t}\left(\rho \tilde{\upsilon }\right)+\frac{\partial }{\partial x_i}\left(\rho \tilde{\upsilon }{u}_i\right)=G_{\upsilon }+\frac{1}{{\sigma }_{\tilde{v}}}\left[\frac{\partial }{\partial x_j}\left\{\left(\mu +\rho \tilde{\upsilon }\right)\frac{\partial \tilde{\upsilon }}{\partial x_j}\right\}+C_{b2}\rho {\left(\frac{\partial \tilde{\upsilon }}{\partial x_j}\right)}^2\right]-Y_v+S_{\tilde{v}}$ (5)

式(5)中， $\tilde{\upsilon }$ 是湍流动粘滞率， $\mu$ 为粘性系数。

求解流场时，采用时间追赶的有限体积法，求解三维定常粘性的雷诺平均N-S方程。空间离散采用中心差分法，时间离散采用四级龙格–库塔法 [8] 。并采用隐式残差光顺法和多重网格技术来加速收敛 [9] 。在前处理模块生成涡轮单通道“HOH”网格 [10] ，主通道沿气流方向有3个网格分区，其中叶片型面附近采用“O”型网格，叶片通道前后延伸段则采用“H”型网格。为了尽量减小网格质量对计算精度的影响，所生成的计算网格能保证所有网格内部各网格边线的夹角均大于18˚，网格长宽比不大于2000，相邻网格膨胀比小于3.4。生成的整体涡轮模型和叶片单通道流场计算网格如图2所示。

(a)(b)

Figure 2. Generated turbine model and grid of single passage

图2. 生成的涡轮模型和单通道网格

分析上述三种情况以及正常状态的涡轮性能。由稳态模型计算得到的边界条件和转速变化见表1。

Table 1. Boundary condition and rotor speed

表1. 边界条件和转速

以不同情况的进口总温改变为例，如图3所示。

Figure 3. Inlet total temperature

图3. 不同情况的进口总温

由图3可知，相比涡轮正常状况，情况3和情况2进口总温增加，其中情况3进口总温增加更为明显，情况1的进口总温下降。可以看出，压气机性能损失会使涡轮总温减小；而涡轮性能损失会使总温升高；当涡轮和压气机性能都损失时，会使总温增加更为明显。涡轮性能下降，产生同样的能量势必要求涡轮进口总温增加；压气机性能下降，涡轮产生的功相对增多，因此进口总温相对减少。

利用表1的数据修改边界条件和相应转速，带入计算得到在不同损失情况的涡轮各级动静叶片总压分布。如图4所示。

由图4可知，涡轮第一级动叶片叶顶部位总压最大，之后总压随涡轮级数的增加而递减。图4(b) (情况1)、图4(c) (情况2)和图4(d) (情况3)相比图4(a)总压无明显变化，主要是进出口性能变化不明显。鉴于实际考虑，压气机第一级动叶片受到的影响最大，以第一级动叶片研究涡轮动叶片流场的变化。如图5所示。

由图5可知，图5(b)、图5(c)和图5(d)比图5(a)的气流分离提前，靠近涡轮叶片前缘，而后进入平稳流动状态。图5(d)表现更为明显。图6为第一级涡轮叶片(压力面)的静压等值线分布图。图7是涡轮叶片50%截面的总压分布图。

由图6可知，图6(a)和图6(b) (情况1)静压等值线分布基本相同，而且静压数值也较一致。图6(c) (情况2)和图6(d) (情况3)较图6(a)和图6(b)静压等值线分布变化不大，但叶片前缘静压数值有较大变化。由图7可知，图7(a)~(d)的涡轮叶片50%截面的总压分布基本一致。由此可以推断出，当部件出现一定幅度的损失，而且这种损失还未使部件性能出现根本变化时，压力场、气流流场不会出现较大程度的改变。图8反应的是涡轮第一级动叶片沿50%截面弦长的总压分布。

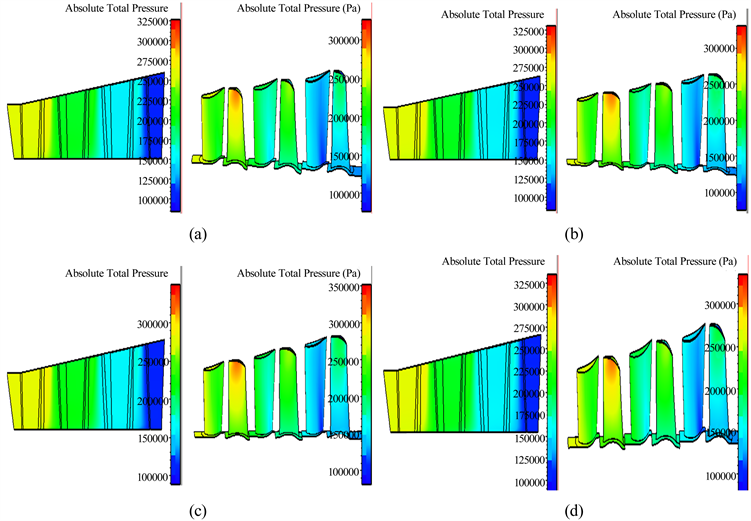
Figure 4. Total pressure distribution in floating field

图4. 不同情况涡轮流场总压分布

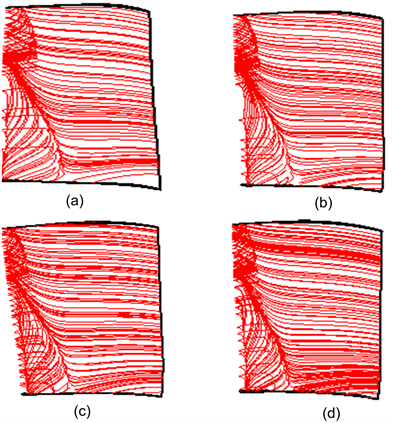
Figure 5. Flow field distribution in rotor blasé of stage 1 (pressure surface)

图5. 涡轮第一级动叶片(压力面)流场分布

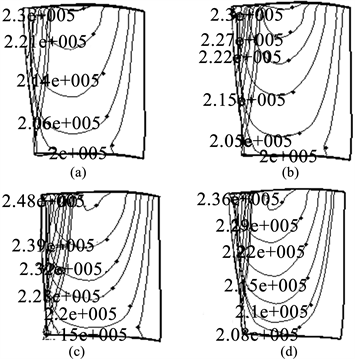
Figure 6. Contour line distribution of static pressure in rotor blade of stage 1

图6. 第一级涡轮动叶片的静压等值线分布

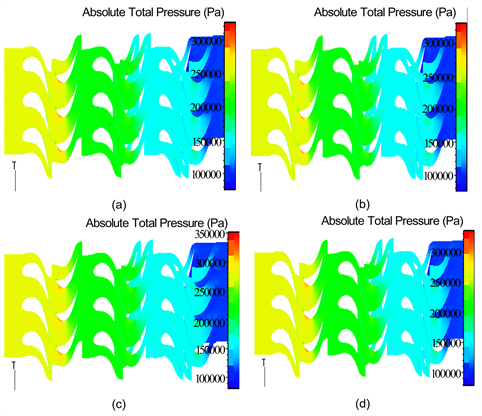
Figure 7. Total pressure distribution in 50% surface of turbine blade

图7. 涡轮叶片50%截面的总压分布

由图8可知，对于涡轮第一级动叶片沿50%截面弦长的总压而言，情况1、情况2和情况3比正常状况都有所升高，情况3升高最为明显，情况1则不明显。涡轮部件性能损失直接作用在自身部件上；而压气机性能损失间接影响到涡轮部件；情况3的性能改变，并不是情况1和情况2对应涡轮性能损失的简单叠加，由于发动机是一个整体，各部件要满足部件匹配关系，两个部件性能发生损失的整机重新在另一个状态点得到平衡，引起的性能损失并不大。总压在叶片弦长中部变化较大，两端较小。各级涡轮特性参数的变化如图9所示。

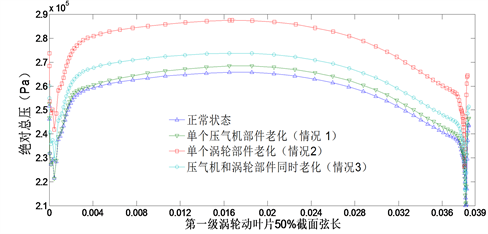
Figure 8. Total pressure distribution in the chord of 50% surface of stage 1 rotor blade

图8. 涡轮第一级动叶片沿50%截面弦长的总压分布

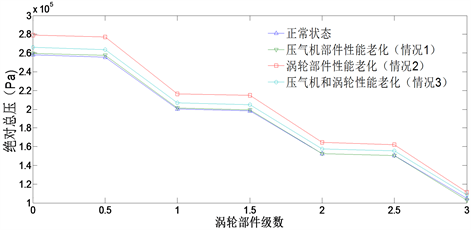
Figure 9. Variation of turbine total pressure in the stage

图9. 涡轮各级总压的变化

由图9可知，涡轮各级总压的变化规律与图8各种情况呈现的变化规律一致。同时注意到，涡轮前面级的性能变化大，后面级变化小。上述部分计算结果与实验结果一致。

5. 结论

本文针对压气机和涡轮核心部件性能衰退开展研究，主要考虑三种情况，分析当单个压气机、涡轮部件自身和两个部件同时老化，对整机中涡轮部件性能的影响。由于损失程度相对不大，气流流场和压力场变化不明显。得到的主要结论如下：

1) 在稳态模型的基础上通过修改进出口边界条件以及转速进行流场仿真。得到两个部件同时老化对于涡轮性能的影响，并不是两个单独部件对涡轮的性能简单叠加，而是受制于各部件之间的相互制约，损失相对来说并不大。

2) 当单个部件或更多出现小幅度损失，而且这种损失还未使涡轮部件性能出现根本变化时，压力场、气流流场并不会出现较大程度的改变。气流分离提前，略靠近叶片前缘，等值压力线分布基本不变，但压力数值增加。

3) 压气机性能损失会使涡轮总温减小；而涡轮性能损失会使总温升高总压在叶片弦长中部变化较大，两端变化较小。对于多级涡轮来讲，在前面级的性能变化大，后面级的性能变化较小。