1. 引言
锚板作为一种高效可靠的锚固系统,广泛应用于输电塔、海上浮动平台、水下管道、隧道等结构,为其提供抗拔力 [1] 。半个多世纪以来,锚板的广泛使用促使研究人员对锚土相互作用有了更深入的了解。锚板的抗拔能力取决于锚的几何形状、埋入深度和土体参数(密度、强度指标)等因素。在之前的数十年里,国内外学者对其极限承载力与土体破裂机制展开了较为系统的研究 [2] - [8] 。例如:茜平一等 [1] 根据试验观察结果,分析了浅埋锚板周边土体的破坏特征。何思明 [2] 研究了条形锚板的抗拔破裂面形状。Murray等 [5] 对砂土中锚板抗拔承载性能进行了研究,并结合极限平衡和极限分析方法给出了锚板承载力的上限解答。Yu [6] 采用空腔膨胀理论和塑性区的发展规律获得了锚板的抗拔承载力。
由于锚板–土体结构相互作用的复杂性,之前的研究结果差异性较大,越来越难以满足锚板设计需求,传统的锚板极限拉拔试验采用砂土作为填料,综合采用透明有机玻璃或钢化玻璃来观测板周围土体破裂面发展情况,模拟平面应变条件下锚板承载特性。但是直接试验结果表明,砂土材料与玻璃之间的摩擦角度一般高于10˚ [9] ,因此该方法得到的破裂面比实际劈裂面小,难以真实模拟平面应变状态。为了克服试验缺陷,钢棒相似土由于试验条件可控、不存在压缩变形等特点,在研究中逐渐得到了应用 [10] - [16] 。
因此,本文在进行充分文献调研的基础上,通过室内模型试验,采用钢棒相似土作为填料,研究了不同埋深比下,锚板的极限拉拔力的变化以及破裂面的变化情况,为水平锚板极限平衡计算模型的建立提供理论依据。
2. 试验设备和步骤
2.1. 试验设备
试验设备主要是连接杆、锚板和模型箱等,如图1。锚板为长方形形钢板,长 × 宽为75 × 100 mm,厚度为10 mm;锚板连接杆可互相串联或拆卸,直径为6 mm;试验所用模型箱为钢板,前面为有机玻璃板,其长×宽×高为500 × 100 × 500 mm。在本锚板拉拔试验中,上拔过程采用位移控制式,由加载设备提供锚板的上拔力。本试验的数据采集系统包括加载设备、压力传感器和计算机等。计算机可以实时监控并记录上拔过程中锚板的拉拔力;本文锚板拉拔速率控制为4 mm/min,当锚板拉拔力稳定后终止试验。在实验过程中,计算机可以自动记录锚板拉拔时的位移及拉力。
为探究锚板上拔过程中破裂面和位移场的变化规律,本文采用粒子测速技术(PIV),该技术是通过对比不同时刻的图像,从而得到拍摄区域内物体运动的轨迹和形变。本文采用GEOPIV8软件,为一段在matlab中运行的代码。通过手动选择如图中所示的分析区域,如图2会在该区域内自动划分多个网格。将拍摄的一系列照片按照时间顺序编号后,从第二张图片开始,matlab自动捕捉每个网格内部中的颗粒相对于第一张图片中该网格内部的颗粒的运动轨迹,直到最后一张照片。计算完毕,手动输入各个选取的参考点的真实坐标,即可得到分析区域内土体的位移矢量以及形变。
2.2. 材料参数
本文采用长为10 cm的钢棒相似土作为锚板拉拔模型试验的填料。钢棒的基本参数见表1所示。

Table 1. Basic parameters of steel rod
表1. 钢棒的基本参数
通过对钢棒间作用机理分析,得出内摩擦角是影响钢棒相似土力学行为的主要参数。结合试验条件,开展了系列剪切试验,测得了钢棒相似土的内摩擦角。剪应力随着剪切位移的增大,先迅速增大,当试样达到抗剪强度后,便趋于稳定且略有下降。垂直压应力越大,其相应的抗剪强度越大。
由图3可知,钢棒相似土更符合无粘性土的特性,其粘聚力基本为0,根据无粘性土的抗剪强度计算公式
,可以得知,在竖向应力σ不变的情况下,内摩擦角的大小决定了土样的抗剪强度。通过曲线的拟合,通过计算其斜率的大小,本文得到如下数据:直径4 mm的钢棒,其内摩擦角为33.9˚,按照表2中计算手册给出的土壤内摩擦角参考标准,其相当于中砂土。

Table 2. Reference standard for soil internal friction Angle
表2 土壤内摩擦角参考标准
3. 结果分析
3.1. 上拔力与位移的关系
锚板拉拔试验中不同埋深比的拉拔力–位移曲线如图4所示。
整个拉拔过程大致可分为三个阶段:① 峰前弹性阶段,② 峰后下降阶段,③ 波动阶段。从图中可以看出,随着埋深比的增加,锚板拉拔力达到峰值的所需位移越大,其增长的拉拔力也越大。在拉拔力下降阶段,埋深比越大,其减小的拉拔力也越大,波动的幅度也越大。极限上拔力随埋深比的增加成几何级数增加,埋深比H/D分别为1、2、3、4时,极限上拔力Qmax分别为84 N、214.8 N、302 N、475 N,
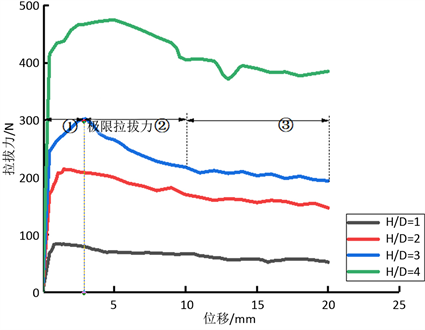
Figure 4. Drawing force-displacement diagram
图4. 拉拔力–位移曲线图
位移δmax分别为1 mm、1.5 mm、2.8 mm、4.9 mm。
3.2. 锚板上拔过程的位移场及破裂面分析
水平锚定板破坏模式主要有三种,如图5所示。第一类破坏面是摩擦柱型 [17] ,该模式下拉拔力由锚杆正上方圆柱形破坏面内土体的重量加上沿该破坏面的摩擦阻力计算得出。由于锚杆周围受扰动的土体质量一般大于锚杆上方的土体,因此,基于这种破坏面,往往低估了锚杆的拉拔能力。第二类破坏面是斜面破坏模式 [18] ,该模式下拉拔能力的计算为倒梯形上土体的重量。由于忽略了沿破坏面摩擦力的影响,Mors方法对浅层锚杆通常过于保守。然而,它高估了深锚的拉拔能力,在这种情况下,破坏面通常延伸不到地面。第三类破坏面是圆弧破裂面型破坏模式 [19] 。

Figure 5. Three failure modes of soil around an anchor plate
图5. 锚板周围土体3种不同破坏模式
为了更好的研究锚板上拔过程中破裂面的形态,本文采用了粒子图像测速技术(PIV)观察锚板上拔过程中的位移场及破裂面,该技术是通过比对不同时刻的图像来监测拍摄区域内物体运动的轨迹和形变。
图6~图9为不同埋深比达到极限拉拔力下的位移矢量图和破裂面云图。当埋深比H/D = 3时,破裂面与竖直方向的夹角为28˚,其角度等于45˚-φ/2,在其余三个埋深比下,破裂面与竖直方向夹角为22˚左右,其角度略小于45˚-φ/2。
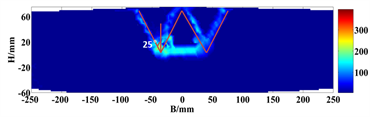
Figure 6. Buried depth ratio H/D = 1
图6. 埋深比H/D = 1
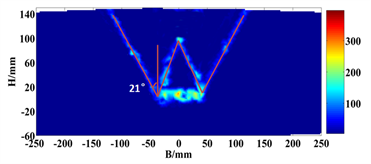
Figure 7. Buried depth ratio H/D = 2
图7. 埋深比H/D = 2

Figure 8. Buried depth ratio H/D = 3
图8. 埋深比H/D = 3

Figure 9. Buried depth ratio H/D = 4
图9. 埋深比H/D = 4
从图中可以看出:锚板在向上拉拔过程中,在锚板上方形成了对称的破裂面,左右剪切区域相似,刚性三角形内的位移竖直向上,当埋深比H/D = 1 (图6)时,刚性三角形顶部发展到填料的顶部,破裂面形状为“W”型;当埋深比H/D = 2 (图7)时,刚性三角形顶部发展到填料高度的1/2处,除了刚性三角形区域内向上位移,其余部分均匀的向两侧移动,破裂面形状为中间凹的“W”型;当埋深比H/D = 3 (图8)时,左右剪切区域相似,刚性三角形顶部发展到填料高度的1/3处,刚性三角形区域内向上位移;当埋深比H/D = 4 (图9)时 ,刚性三角形顶部发展到填料高度的1/4处。
通过分析可知:不同埋深比下,刚性三角形的形状和大小一致,随着埋深比的增加,其上方受扰动较小的区域增加,位移量增量大的范围会减小。所以,埋深比对锚板拉拔力有较大影响,该试验结果可为锚板上拔预测模型建立以及设计提供参考依据。
3.3. 锚板大位移上拔破裂面的演化
为了更好探究上拔位移量对破裂面的影响情况,以埋深比H/D = 3为例,分析锚板在大位移情况下破裂面的演化情况,如图10。
 (a) 位移1 mm (b) 位移3 mm
(a) 位移1 mm (b) 位移3 mm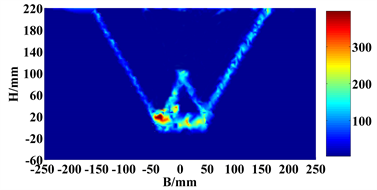 (c) 位移15 mm
(c) 位移15 mm
Figure 10. Evolution of fracture surface cloud map during large displacement uplift of anchor plate
图10. 锚板大位移上拔过程破裂面云图演化
从图中可以看出:当位移1 mm时,破裂面首先发展到填土高度的1/2处;当位移3 mm时,破裂面已延伸到填土表面,刚性三角形也显现出形状,此时锚板拉拔力已达到峰值。随着上拔位移的增加,破裂面和刚性三角形越来越明显。
4. 结论
采用钢棒相似土替代传统砂土,通过系列模型试验,基于PIV图像分析,对锚板在钢棒相似土中的抗拔特性进行系统的试验研究,得出以下结论:
1) 采用钢棒相似土,将平面应变试验简化为二维试验条件,消除了前后挡板摩擦力的影响,直径4 mm的钢棒,其内摩擦角为33.9˚,相当于中砂土。
2) 整个拉拔过程大致可分为三个阶段:① 峰前弹性阶段,② 峰后下降阶段,③ 波动阶段。随着埋深比的增加,锚板拉拔力达到峰值的所需位移越大,其增长的拉拔力也越大。
3) 锚板在向上拉拔过程中,在锚板上方形成了对称的破裂面,左右剪切区域相似,刚性三角形内的位移竖直向上,试验结果可为水平锚板极限平衡计算模型建立提供参考。
4) 不同埋深比下,刚性三角形的形状和大小一致,随着埋深比的增加,其上方受扰动较小的区域增加。破裂面与竖直方向的夹角大致等于45˚-φ/2。