一种基于MATLAB的改进的水准网平差程序设计与实现

Design and Implementation of a Leveling Net Adjustment Program Based on MATLAB

摘要: 为了高效准确地计算水准网数据，通过分析水准网的数据结构，对常规的MATLAB水准网平差程序做了进一步的改进，重点研究了已知水准点点名为字母的情况下，误差方程系数矩阵与常数项的建立方法。基于间接平差原理使用GUI功能实现了水准网平差。解决了一般的MATLAB平差程序中需要手动替换点名才能平差的问题。实验引入实例数据证明了程序的正确性与实用性，对MATLAB测绘数据处理有一定的参考与指导意义。

Abstract: In order to calculate the leveling net data efficiently and accurately, by analyzing the data structure of leveling net, a further improvement is made to the adjustment program of MATLAB leveling net. Based on the principle of indirect adjustment, GUI function is used to implement leveling network adjustment. It solves the problem that in the general MATLAB adjustment program, it needs to manually replace the name to adjust. The application of real data in the experiment proves the correctness and practicability of the program, which has certain reference and guiding significance for MATLAB mapping data processing. 

1. 引言

MATLAB是一个强大的数学软件，其出色的矩阵处理能力，丰富的图形图像处理功能，以及简介化的程序语言为当今测绘领域提供了独具特色的研究手段。图形用户界面(Graphical User Interface, GUI)，是MATLAB的人机交互式界面设计功能。利用GUI设计可视化界面，解决测绘中的数据处理与平差问题是近几年的研究热点 [1] [2] [3] 。

在水准测量中，已知水准点通常由字母或字母与数字组合命名，未知水准点由起始水准点到目标水准点方向，以数字1, 2, 3……顺序编定点号 [4] 。所以，在一般的水准网中，水准点可分为以字母命名的已知水准点和以数字命名的待测水准点两类。文献中李建章采用调用函数的方法，以简洁的语言在MATLAB环境下实现了水准网平差；王鹏磊、刘长星将MATLAB的GUI功能应用到了水准网平差上，实现了平差的可视化 [5] [6] 。但是以上平差程序不能对包含字母点名的水准网平差。应对含有字母点名的水准网时，需要手动把字母点名替换成数字参与平差。这种方法虽然程序代码量少，降低了编程难度，但纯数字形式容易造成与实际测量数据混乱或者错误匹配的情况，甚至当数据量特别大时，需要大量时间把字母点号改成数字再平差，工作量大而且易错，对测量数据处理造成了一定的阻碍。

为了解决这个问题，在分析了大量水准网数据基础上，针对数据中包含字母点号这一问题，重点研究了基于间接平差原理的点位概略高程计算和误差方程系数矩阵的建立。设计程序以EXCEL文件录入待平差的观测数据。以常规的数值矩阵计算操作结合元胞数组的处理方式，应用字符串比较函数实现概略高程赋值，解决字母点名问题的同时，能够快速建立误差方程系数矩阵与常数项，实现复杂网型的水准网平差。

2. 水准网间接平差原理

间接平差因构建简单，直接计算平差参数，与程序的相容性良好等特点，被广泛应用于平差数据处理中。间接平差直接假设t个未知参数，列出n个观测值方程，进而列出误差方程组。基于最小二乘原理求解自由极值得到法方程，解算未知参数获得平差值 [7] 。

最小二乘原理：

$V^{\text{T}}PV=\min$ (1)

间接平差其函数模型为：

$$ (2)

误差方程：

$V=B\hat{x}-l$ (3)

其中B为误差方程系数矩阵，l为常数项。

间接平差法方程：

$N_{BB}\hat{x}-W=0$ (4)

其中，， $N_{BB}=B^{\text{T}}PB$ 。

间接平差解为：

$\hat{x}=N_{BB}^{-1}W$ (5)

3. 程序模块设计与实现

3.1. 可视化界面设计

利用GUI图形用户界面设计可视化窗体程序，美观便捷的同时能够提升数据处理的效率。实验程序主要应用的GUI控件有“按钮(pushbutton)”、“可编辑文本(edit)”、“单选按钮(radiobutton)”和“表格(uitable)”等。程序代码写在按钮的回调函数(callback)下，通过鼠标点击执行；可编辑文本与表格用来显示主要平差数据；单选按钮提供两种定权方式的选择。程序设计界面如图1所示。

Figure 1. Interactive interface design

图1. 交互式界面设计

前两个按钮录入已知点数据和观测数据，点击第三个按钮执行平差；三个界面表格分别用以显示已知数据、观测数据和平差结果。数据导入和平差计算两部以MATLAB的set函数将执行结果显示在界面上，用以检核或者编辑，提升程序的正确性与可靠性。

3.2. 数据的组织与录入

水准网数据分为已知水准点数据和未知点的观测数据两类。为了方便区分，程序设计两个数据读取接口分别导入。已知点的数据结构简单，仅由点名和高程两列构成。而观测数据的一条测边包含一个观测起点，一个观测终点，一个高差值和一个权值。因此，观测数据以起点，终点，高差，距离或测站数的顺序设计成4列，编制成两个EXCEL表格文件通过xlsread函数数据录入数据。xlsread函数能够在录入数值型和字符型数据的同时对两者进行分离，可以降低误差方程系数矩阵建立的难度。关键代码：

[num,txt,wz_all]=xlsread(wzd_filepath);

shift=num(:,1:2);

EXCEL 导入函数xlsread将导入的数据分为分离成三类。数据中的字符元素在导入时被直接剔除，只保留数值元素建立num数值矩阵，而从EXCEL读取到数据后，对数据进行一些预处理，包括点号矩阵，高程，高差向量的提取；已知点，未知点个数的计算等，以便进行概略高程计算，其中赋值建立的shift为起点号与终点号两列组成的数值矩阵，不含字符元素，下文中用以计算未知点概略高程。

3.3. 概略高程计算

基于MATLAB设计水准网平差，主要的难点在于如何计算概略高程并建立误差方程系数阵与常数项，特别是当已知水准点的点名为字母时，录入的数据为cell格式的元胞数组，需要同时处理数值型元素与字符型元素，增加了程序设计难度，所以程序在数据类型的处理上，多处以字符型元素为对象，采用处理字符串的方式设计程序代码。

为计算概略高程，程序先引入一个存放概略高程的工具阵matrix。在实际测量数据数据处理中由于点号命名方式由数字和字母共同组成。一般的矩阵加减数值运算在此处基本无效。所以通过设计循环，采用查找点名的方式先对已知点的高程进行赋值，进而建立起算边(测边的一个端点的高程已知为起算边)。赋值方法如图2所示，其中第一个元胞数组由起点号和终点号两列构成；第二个为已知点数据。

Figure 2. Assignment method

图2. 赋值方法

其中前两组数据因包含字母，EXCEL导入后均为元胞数组。元素数据类型不同无法进行常规的数值计算。所以程序先从已知点数据提取一个字母点号A，建立循环以strcmp函数与第一个元胞数组的元素逐个对比。如果对比结果相同，matrax对应的元素进行赋值；不同的则跳过，直到所有已知点赋值完毕。

已知点初始高程赋值后，继续对未知点的概略高程赋值。总体技术路线如图3所示。

以循环对matrix逐行遍历。如果发现matrix的一行仅有一个元素为空，则将此边判定为起算边。起点概略高程已知，终点概略高程未知，则加上对应观测的高差；反之，则减去对应观测的高差。以条件句进行判断，计算另一点的概略高程并进行变量赋值。总的来说，就是以初始已知高程为起算数据计算测段内相邻点高程；再将已经算得高程的点作为已知点重复计算，直到所有未知点的概略高程全部赋值。未知点概略高程计算流程如图4所示。

Figure 3. General technical route

图3. 总体技术路线

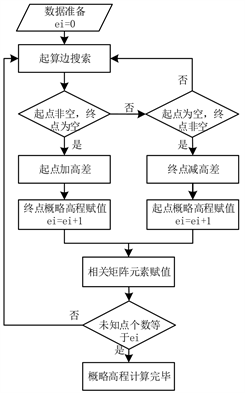
Figure 4. Approximate elevation of unknown points

图4. 未知点概略高程计算

3.4. 法方程系数矩阵与常数阵的构建

水准网平差中的误差方程组由系数阵B，参数 $\hat{X}$ 和常数项l构成。一个误差方程对应一条测边，只有当一条边的端点为未知点时，才能使对应系数体现为1或−1，当起点为未知点时，对应系数为−1；终点为未知点时，对应系数为1。误差方程常数项l可由测边两端点的概略高程直接相减获得，即由上述已经赋值的matrix两列元素对应相减直接计算 [8] ；关于权阵的计算，程序以平均距离观测的高差为单位权观测，或以平均测站数观测的高差为单位权观测定权，建立权阵P。系数矩阵B，权阵P，常数项l都建立完毕，则根据间接平差法方程计算平差值。

4. 实验测试

为了检测程序代码设计的正确性与实用性。利用某工程的水准网数据测试程序 [9] ，水准网如图5所示。分析此工程水准网，已知水准点为A、B、C三点，未知点分别为1、2、3，针对以上6个水准点共进行了7次高差观测，观测的高差数据分别为h₁~h₇。

Figure 5. Leveling network

图5. 水准网

已知水准点的数据如表1所示，观测数据如表2所示。已知水准点的点名全部用字母表示，未知水准点点名以序号1、2、3表示。已知点以点号和高程组织两列，观测数据以起点，终点，观测高差，距离组织四列，编辑两个EXCEL文件导入进行平差。

Table 1. The point data

表1. 已知点数据

Table 2. Observation data

表2. 观测数据

程序将平差后的结果输出后，与原参数平差值对比，对比结果相同。最终平差结果对比如表3所示。

Table 3. Adjustment results were compared

表3. 平差结果对照

5. 结束语

本文在分析水准网数据特点的基础上，发现常规的MATLAB水准网平差程序的局限性，即需要替换点名才能平差。针对这一问题，对水准网平差程序做了进一步改进，在实现数据平差与操作可视化的同时，解决了MATLAB水准网平差中需要手动替换点名的问题，为外业数据提供了较为简便高效的处理方法，提升了水准网平差的效率与可靠性。并在一定程度上提供了一种较为可靠的处理字符型数据的方法，对MATLAB测绘数据处理有着一定的指导与参考意义。