中值滤波分析改进的多元线性回归算法对MBR污泥龄的计算

Median Filter Analysis Improved Multiple Linear Regression Algorithm for the Calculation of MBR Sludge Age

摘要: 用MBR系统进行污水处理时，经常会遇到有大量的污泥被截留在膜表面的现象，该现象会造成膜污染， 影响MBR系统处理污水的效果。研究发现，通过预测MBR系统的污泥龄，可以使工作人员及时采取相应措施来控制膜污染，以此来达到减缓膜污染的目的。为了解决该问题，本文首先利用多元线性回归算法对MBR系统中的污泥龄进行预测，但是误差稍大。然后采用中值滤波分析改进的多元线性回归算法预测污泥龄，预测结果表明，改进后的算法更准确，与实际值误差更小，解决了准确预测污泥龄的问题，对提高MBR系统处理污水效果具有一定的参考价值。

Abstract: When MBR system is used for sewage treatment, it is often encountered that a large amount of sludge is trapped on the surface of the membrane, which will cause membrane pollution and affect the effectiveness of MBR system in sewage treatment. It is found that by predicting the sludge age of MBR system, the staff can take corresponding measures to control membrane pollution in time, so as to achieve the purpose of reducing membrane pollution. In order to solve this problem, multiple linear regression algorithm was first used to predict sludge age in MBR system, but the error was slightly larger. Then the improved multiple linear regression algorithm is used to predict the sludge age by median filter analysis. The result shows that the improved algorithm is more accurate and has a smaller error with the actual value, which solves the problem of accurately predicting the sludge age and has certain reference value for improving the sewage treatment effect of MBR system.

1. 引言

近年来污水处理成为热点话题之一，污水处理有很多种方法，而利用MBR进行污水处理是其中比较高效的方法之一 [1] 。MBR是一种将高效膜分离技术与活性污泥生物处理单元相结合的水处理装置。MBR系统由各个膜组件连接组成，在MBR系统运行时污水流过各个膜组件，过滤掉大分子颗粒以此来达到过滤污水的目的。但是随着系统的运行会有大量的污泥被截留在膜表面，这些被截留的污泥会造成膜污染 [2] ，从而影响膜组件的寿命和处理污水的效果。

大量研究表明污泥龄(SRT)是MBR运行的重要控制条件之一 [3] ，它决定着反应器的污泥负荷和微生物的运行状态。一般来说，年轻的污泥活性高，分解代谢有机污染物的能力强，但凝聚沉降性能较差；而年长的污泥有可能已老化，分解代谢能力较差，但凝聚沉降性能较好。通过预测SRT，可以选择合适的微生物年龄，使活性污泥既有较强的分解代谢能力又有良好的沉降性能。可以有效地减少截留在膜表面的污泥，达到减缓膜污染的目的。本文采用中值滤波分析改进的多元线性回归算法来预测污泥龄，多元线性回归算法 [4] 非常适用于数据预测分析，并且它的泛化能力比较好，但是多元线性回归算法存在预测结果误差稍大的问题，而中值滤波分析 [5] 可以对训练样本数据做去噪预处理操作，能够提高预测结果的精度。

2. 使用线性回归算法和中值滤波分析算法

2.1. 线性回归算法

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，能够用一个直线较为精确地描述数据之间的关系。

2.1.1. 一元线性回归算法

一元线性回归算法又叫直线拟合算法，一元线性回归算法是研究一个自变量与一个因变量之间相关关系的算法，它是研究两个变量相关关系的最简单模型。在一元线性回归模型中，如果 $x_i$ 与 $y_i$ 存在相关关系，则建立一元线性回归模型 $\left(y_i=\alpha +\beta x_i+{\gamma }_i,i=1,2,\cdots ,n\right)$ 和一元线性回归方程 $\hat{y}=a+bx$ 。其中 $\left(\alpha +\beta x_i\right)$ 表示 $x_i$ 与 $y_i$ 之间的相关关系， ${\gamma }_i$ 表示外界影响因素的总和，也叫做随机误差；b为回归直线的斜率，a为回归直线的截距。在求解a，b时，我们用最小二乘法来计算a，b，即 $Q\left(\alpha ,\beta \right)={\displaystyle \sum {\gamma }_i^2}=\min$ ，经计算可得到a，b。

在计算出一元线性回归方程后，为了验证所建立一元线性回归方程的正确性，还需要计算误差。在一元线性回归算法中，我们可以利用拟合度的大小来衡量误差的大小，拟合度表示实际数据点在回归直线 $\hat{y}=a+bx$ 周围的紧凑程度，紧凑程度越大，则误差就会越小，反之则相应的误差就会越大。

2.1.2. 多元线性回归算法

多元线性回归算法 [6] 它是研究多个自变量与一个因变量之间相关关系的算法。多元线性回归算法和一元线性回归算法的原理类似，如果这些变量之间存在相关关系，则建立多元线性回归模型(公式(1))和多元线性回归方程(公式(2))。

$y_i={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_{m-1}{x}_{m-1}+\gamma$ (1)

$\hat{y}=b_0+b_1{x}_{i,1}+b_2{x}_{i,2}+\cdots +b_{m-1}{x}_{i,m-1},i=1,2,\cdots ,n$ (2)

令 $\beta ={\left({\beta }_0,{\beta }_1,\cdots ,{\beta }_{m-1}\right)}^{\text{T}}$ ， $\hat{\beta }={\left(b_0,b_1,\cdots ,b_{m-1}\right)}^{\text{T}}$ ， $\gamma ={\left({\gamma }_0,{\gamma }_1,\cdots ,{\gamma }_{m-1}\right)}^{\text{T}}$ ，其中 $\beta$ 是未知参数向量， $\gamma$ 为误差向量；令 $Y={\left(y_1,y_2,\cdots ,y_n\right)}^{\text{T}}$ ，X为方程(1)的设计矩阵。把方程(1)写成矩阵的形式： $Y=X\beta +\gamma$ ，然后我们要做的就是求解 $\hat{\beta }$ 了。同一元线性回归算法一样，利用最小二乘算法来求解向量 $\hat{\beta }$ ，经过计算得到 $\hat{\beta }={\left(X^{\text{T}}X\right)}^{-1}{X}^{\text{T}}Y$ 。

在多元线性回归算法中计算误差时，同样可以利用拟合度的大小来衡量误差的大小，在这里我们利用相关系数R的大小来衡量拟合程度，其中 $0\le R\le 1$ 。当相关系数R趋向于1时，那么说明算法的拟合度高，相应的误差就越小，反之算法的拟合度低，相应的误差就越大。

2.2. 中值滤波分析

中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。

中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术，中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替，让周围的像素值接近的真实值，从而消除孤立的噪声点 [7] 。

2.2.1. 一维中值滤波

中值滤波是非线性滤波方式，依靠模板来实现，设模板尺寸为M，M = 2r + 1，模板半径是r。若一维信号为 $\left\{f_i\right\},i=1,2,\cdots ,N$ ，则输出为：

$g_j=\text{medium}\left[f_{j-r},f_{j-r+1},\cdots ,f_j,f_{j+r}\right]$

medium表示中值，即信号序列在模板中的排列顺序，取排在最中间的值，有 $1<j-r<j+r<N$ 。上式可通过滑动奇数长度的模块来实现。

2.2.2. 二维中值滤波

在二维情况下，设有一个m × m的二维中值滤波窗口(m为奇数)，需要滤波的图像为f(x, y)，点(x, y)处的中值滤波是从输入图像中输出以(x, y)为中心的滤波窗口中m × m个点[…]。

$g\left(x,y\right)=\underset{x_0,y_0\in s}{\text{medium}}\left[f\left(x_0,y_0\right)\right]$

式中，S为窗，中心坐标为(0, 0)。

2.3. 中值滤波分析去噪算法步骤

(1) 选取两层尺度，对含噪图像进行二维小波变换，得到高频子带和低频子带图像。

(2) 采用3 × 3窗口，单位距离为半径，对低频子带图像进行均值滤波。

设图像的像素灰度值为w(j, k)，均值滤波后，输出为：

$\bar{w}\left(j,k\right)=\frac{1}{L}{\displaystyle \underset{\left(x,y\right)\in A}{\sum }w\left(x,y\right)}$

式中，A表示窗口像素组成点的集合，L表示像素数。

(3) 对各高频子带图像进行中值滤波。

(4) 对中值滤波后的高频子带图像进行阈值处理。

(5) 各高频子带图像在量化阈值时，也在进行系数增强。较大的增强系数在高尺度下的子带图像中选择，较小的增强系数在低尺度下的子带图像中选择，可由噪声与尺度变化的关系得到。

(6) 再对w(j, k)迸行小波逆变换，得到降噪后的输出图像。

3. 多元线性回归算法在MBR系统中对污泥龄的计算

3.1. 多元线性回归算法对污泥龄的计算

在MBR系统中，我们可以通过预测污泥龄SRT (θ_x)来选择合适的微生物年龄，使MBR系统中的活性污泥既有较强的分解代谢能力又有良好的沉降性能，影响SRT的主要因素有X (微生物浓度)，Y₀ (污泥表观产率)，HRT (水力停留时间)，c_i − c_e (进出水COD浓度差)和c_i − c_sup (进水与上清液COD浓度差)。

${\theta }_x=\frac{\text{HRT}\left[X+Y_0\left(c_i-c_{sup}\right)\right]}{Y_0\left(c_i-c_e\right)}$

在模拟实验中，我们创建图1所示的模型来预测泥龄θ_x。首先生成1000条θ_x样本数据和理论的来训练多元线性回归模型，把这1000条数据组成训练数据集矩阵X和矩阵Y，其中1000条序列(X, Y₀, HRT, c_i − c_e, c_i − c_sup)组成的样本数据存放在矩阵X中，1000条(θ_x)组成的样本数据存放在矩阵Y中，然后利用最小二乘法计算出 $\hat{\beta }$ ，最后再计算得出多元线性回归方程。

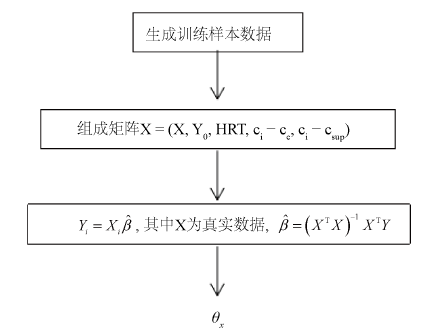
Figure 1. Prediction model of sludge age

图1. 污泥龄预测模型

3.2. 计算结果分析

本文选取了某污水处理厂稳定状态下的数据和图1所示的模型来进行测试，把用于测试的数据分组，对每组数据分别用图1所示的模型来预测污泥龄，然后将预测结果和真实数据做对比，结果表明该模型的误差较大，如表1所示。

Table 1. Comparison table of SRT simulation under stable state (30˚C)

表1. 稳定状态下SRT的模拟计算分析对比表(30℃)

4. 中值滤波分析改进多元线性回归算法在MBR中对污泥龄的计算

4.1. 用中值滤波分析来优化多元线性回归算法

前面用到的多元线性回归算法需要生成一个训练数据集矩阵X来训练模型，但这样得到的模型在做预测分析时误差稍大，这是因为训练数据集矩阵X中的数据分布不均匀，所以我们要对训练数据集矩阵X做去噪预处理，使数据分布均匀，以此来达到提高模型泛化性和减小误差的目的。对训练数据集矩阵X去噪有三个步骤，第一步对矩阵X进行小波分解，得到小波变换 [8] 系数；第二步对小波变换系数进行阈值处理，即用先估计的一个阈值T对小波系数进行比较处理，当小波系数的幅值|w| < T时，将小波系数置为零；否则，不做处理或对其进行收缩。第三步进行逆小波变换，重构得到去噪后的图像。然后再利用X’来做多元线性回归算法来预测θ_x，如图2所示。

Figure 2. Improved sludge age prediction model

图2. 改进后污泥龄预测模型

4.2. 计算结果分析

本文选取了某污水处理厂稳定状态下的数据并利用该模型进行模拟计算。把用于测试的数据分组，对每组数据分别用图2所示的模型来预测污泥龄，经过计算得到的预测值如表1所示，发现改进后的预测值与实际值误差更小，达到了利用中值滤波分析改进的多元线性回归算法对污泥龄做准确预测的目的。

Figure 3. Relationship between actual and predicted SRT values

图3. SRT实际值与预测值关系图

5. 结论

本文研究了在稳定状态下中值滤波分析改进的多元线性回归算法对MBR中污泥龄的预测，在研究过程中我们分别利用多元线性回归算法和中值滤波分析改进后的多元线性回归算法来计算污泥龄。图3所示的分别为污泥龄的实际值、线性回归算法得到的预测值以及中值滤波分析改进后得到的预测值。通过观察发现多元线性回归算法预测的结果精度较低，误差偏大，经过中值滤波分析改进后的多元线性回归算法预测的结果精度更高，误差更小。将该算法应用在MBR系统的污泥龄预测中，能够较准确地预测污泥龄，对MBR领域的研究具有一定的参考价值。

基金项目

国家自然科学基金项目(51378350)；国家自然科学基金青年科学基金资助项目(50808130)；国家自然 科学基金青年科学基金项目(21506159)。