利用统计软件分析重修率与低收入家庭学生的百分比之间的关系

Using Statistical Software to Analyze the Relationship between the Rehabilitation Rate and the Percentage of Low-Income Students

摘要: 2006年7月23日，休斯敦Chronicle发表了题为Reading: First-Grade Standard Too Tough for Many的文章，称“部分人认为更多学生(横跨得克萨斯州)都不必重修一年级，而专家认为应该让贫困地区的学生重修一年级。”该文章介绍的数据为2004~2005年和1994~1995年每个在得克萨斯州61个县的学生：Y = 一年级学生重修率，X = 低收入家庭学生百分比。这些数据来自于书中网站上的文件HoustonChronicle.csv。用R语言采用协方差分析来决定：1) 一年级学生重修率与低收入家庭学生百分比之间的关系；2) 1994~1995年和2004~2005年一年级学生重修率的差异；3) 1994~1995年和2004~2005年一年级学生重修率与低收入家庭学生百分比之间关系的差异。

Abstract: On July 23, 2006, the Houston Chronicle published an article entitled “Reading: First-Grade Stand-ard Too Tough for Many”. The article claimed in part that “Some people think that more students (across Texas) do not have to rehabilitate the first grade, and experts believe that students in poor areas should be rebuilt in the first grade.” The article presents data for each of 61 Texas counties on Y = Percentage of students repeating first grade x = Percentage of low-income students for both 2004~2005 and 1994~1995. The data can be found on the book web site in the file HoustonChronicle.csv. Analysis of covariance is used to decide whether: 1) an increase in the per-centage of low income students is associated with an increase in the percentage of students re-peating first grade; 2) there has been an increase in the percentage of students repeating first grade between 1994~1995 and 2004~2005; 3) an association between the percentage of students repeating first grade and the percentage of low-income students differs between 1994~1995 and 2004~2005.

1. 引言

重修率与低收入家庭学生的百分比之间的关系是我们现在教学必须研究的课题，本文采用R语言程序强大的绘图功能描述它们之间的差异，采用协方差分析方法，结合理论与数学模型，在图形与命令结果中直观地看出它们的差异，为以后教学的研究提供可行性借鉴。

本次论文在方法的使用与模型的构造上都使用协方差分析方法，是在线性回归的基础上做主要的方差分析 [1] ，最终结果用偏F检验，同时在R程序命令中以图形显示。

2. 单因子方差分析

2.1. 数学模型

设试验只有一个因子(又称为因素) A有r个水平 $A_1,A_2,\cdots ,A_r$ ，现在水平 $A_i$ 下进行 $n_i$ 次独立预测，得到观测数据为 $X_{ij},j=1,2,\cdot \cdot \cdot ,n_i,i=1,2,\cdot \cdot \cdot ,r$ ，则单因素模型 [2] 可表示为

$X_{ij}=\mu +{\alpha }_i+{\epsilon }_{ij},i=1,2,\cdot \cdot \cdot ,r,j=1,2,\cdot \cdot \cdot ,n_i$

${\epsilon }_{ij}~N\left(0,{\sigma }^2\right)$ ，且 ${\epsilon }_{ij}$ 独立，

其中 $\mu$ 为总平均， ${\alpha }_i$ 是第i个水平的效应， ${\epsilon }_{ij}$ 是随机误差。若 $n_1=n_2=\cdot \cdot \cdot =n_r$ ，称模型是平衡的，否则称为非平衡的。

我们的目的是要比较因素A的r个水平的京郊是否有显著差异，这可归结为检验假设 $H_0:{\alpha }_1={\alpha }_2=\cdot \cdot \cdot ={\alpha }_r\leftrightarrow H_1:{\alpha }_1,{\alpha }_2,\cdot \cdot \cdot ,{\alpha }_r$ 不全相等。

如果 $H_0$ 被拒绝，则说明因素A的各水平的效应之间有显著的差异，否则，差异不明显。

按照方差分析的思想，将总离差平方和分解为二部分，即

$S{S}_T=S{S}_E+S{S}_A$

其中

$\begin{array}{l}S{S}_T={\displaystyle \underset{i=1}{\overset{r}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\left(X_{ij}-\bar{X}\right)}^2}},\bar{X}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{r}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{X}_{ij}}},\\ S{S}_E={\displaystyle \underset{i=1}{\overset{r}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\left(X_{ij}-\overline{X_i}\right)}^2}},\overline{X_i}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{r}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{X}_{ij}}},\\ S{S}_A={\displaystyle \underset{i=1}{\overset{r}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\left(X_i-\bar{X}\right)}^2}}\end{array}$

这里称 $S{S}_T$ 为总离差平方和(或称总变差)，它是所有数据 $X_{ij}$ 与总平均值 $\bar{X}$ 之差的平方和，描绘所有观察数据的离散程度； $S{S}_E$ 为误差平方和(或组内平方和)，是对固定的i，观测值 $X_{i1},X_{i2},\cdots ,X_{in}$ 之间的差异大小的度量。 $S{S}_A$ 为因素A的效应平方(和或组间平方和)，表示因子A各水平下的样本均值和总平均值之差的平方和。

可以证明，当 $H_0$ 成了时

$\frac{S{S}_E}{{\sigma }^2}~{\chi }^2\left(n-r\right),\frac{S{S}_A}{{\sigma }^2}~{\chi }^2\left(n-1\right)$ ,

且 $S{S}_A$ 与 $S{S}_E$ 独立。于是

$F=\frac{S{S}_A/\left(r-1\right)}{S{S}_E/\left(n-1\right)}~F\left(r-1,n-1\right)$

若 $F>F_{\alpha }\left(r-1,n-r\right)$ ，则拒绝原假设，认为因素A的r个水平有显著差异，反之“接受”原假设。这也可以通过检验的p值来决定是接受还是拒绝原假设 $H_0$。

2.2. 对低收入家庭学生百分比建立数学模型

我们对X(低收入家庭学生的百分比)划分为1994年份和2004年份两部分，设它们分别为 $A_1,A_2$ ，均值分别为 $\overline{X_1},\overline{X_2}$。由R程序输出结果为：

summary(aov.mis)

Df Sum Sq Mean Sq F value Pr (>F)

A 1 301300.90.8280.365

Residuals120 43606363.4

说明：上述结果中，Df表示自由度；sum Sq表示平方和；Mean Sq表示均方和；F value表示F检验统计量的值，即F比；Pr (>F)表示检验的p值；A就是因素A；Residuals为残差。

可以看出P = 0.365 > 0.05，说明不能拒绝原假设，即认为两个年份低收入家庭学生百分比没有较大的显著差异。

通过函数plot( )绘图可直观描述两个年份低收入家庭学生百分比之间的差异，R程序中运行：plot(miscellany$X~miscellany$A)。

得到图1，从图形上也可以看出，两个年份低收入家庭学生百分比没有较大的显著差异。

2.3. 对一年级学生重修率建立数学模型

我们对Y (一年级学生重修率)划分为1994年份和2004年份两部分，设它们分别为 $B_1,B_2$ ，均值分别为 $\overline{Y_1},\overline{Y_2}$。由R程序输出结果为：

summary(aov.mis)

Df Sum SqMean Sq F value Pr (>F)

B 1 37.837.792.309 0.131

Residuals 120 1964.416.37

可以看出 $F=2.309<F_{0.05}\left(2-1,122-2\right)$ ，或者 $p=0.131>0.05$ ，说明没有理由拒绝原假设，即认为两个年份一年级学生重修率没有显著差异。

通过函数plot( )绘图可直观描述两个年份一年级学生重修率之间的异同，R程序中运行：plot(miscellany$Y~miscellany$B)

得到图2，从图形上也可以看出，两个年份一年级学生重修率没有显著差异：

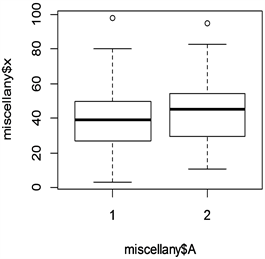
Figure 1. Percentage box chart for low-income families in two years

图1. 两个年份低收入家庭学生百分比箱型图

Figure 2. Two-year first-year student rework rate box chart

图2. 两个年份一年级学生重修率箱型图

3. 协方差分析

协方差的原理

考虑在此我们想模拟一个响应变量的情况下，即在变量Y基础上作连续预测，X和一个虚拟变量d。假设X上的效果Y是线性的。这种情况的通常所说的最简单的版本协方差分析 [2] ，因为预测包括两个定量变量(即，X)和定性变量(即，d)所示。

重合回归线：最简单的模型在给定的情况是在该虚设变量Y上没有影响，也就是：

$Y={\beta }_0+{\beta }_{1}X+\epsilon$

和回归线是完全相同的哑的两个值变量。

平行回归线：另一种模式来考虑这个情况是在该虚拟变量只产生Y中的哑变量的变化，即：

$Y={\beta }_0+{\beta }_{1}X+{\beta }_{2}d+\epsilon =\{\begin{array}{l}Y={\beta }_0+{\beta }_{1}X+\epsilon ;d=0\\ Y={\beta }_0+{\beta }_{1}X+{\beta }_2+\epsilon ;d=1\end{array}$

在这种情况下，回归系数 ${\beta }_2$ 测量在Y，主要是由于哑变量改变虚拟变量。

回归线与截距相等，但不同的斜率：第三个模型考虑这种情况是在其中的虚拟变量X只改变Y大小的效果，也就是说：

$Y={\beta }_0+{\beta }_{1}X+{\beta }_{3}dX+\epsilon =\{\begin{array}{l}Y={\beta }_0+{\beta }_{1}X+\epsilon ;d=0\\ Y={\beta }_0+\left({\beta }_1+{\beta }_3\right)X+\epsilon ;d=1\end{array}$

不相关的回归线：最普遍的模式是哑变量的变化能改变适当的虚拟变量Y，也改变在X变量的基础上Y的大小。在这种情况下，合适的模型是：

$Y={\beta }_0+{\beta }_{1}X+{\beta }_{2}d+{\beta }_{3}dX+\epsilon =\{\begin{array}{l}Y={\beta }_0+{\beta }_{1}X+\epsilon ;d=0\\ Y={\beta }_0+{\beta }_2+\left({\beta }_1+{\beta }_3\right)X+\epsilon ;d=1\end{array}$

在不相关的回归线模型，回归系数 ${\beta }_2$ 能对Y提供一点变化主要是由于哑变量d，然而回归系数 ${\beta }_3$ 改变在变量X的基础上Y的大小也是由于哑变量d。

4. 协方差分析方法的实例分析

4.1. 一年级学生重修率与低收入家庭学生百分比之间的关系

由于协方差分析是建立在线性回归分析和基本的方差分析的基础上，于是我们先对Y (一年级学生重修率)和X (低收入家庭学生的百分比)做线性处理，分析X、Y之间的联系。使用函数：lm(formula = y ~ 1 + x)

在R程序中运行结果如下：

Call:

lm(formula = y ~ 1 + x)

Residuals:

Min 1QMedian 3Q Max

−8.9845 −2.5072 −0.4184 1.850511.1067

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 2.91419 0.83836 3.476 0.000709 ***

x 0.07550 0.01823 4.141 6.47e−05 ***

---

Signif. codes:0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.821 on 120 degrees of freedom

Multiple R-squared:0.125, Adjusted R-squared:0.1177

F-statistic: 17.14 on 1 and 120 DF,p-value: 6.472e-05

结论：从上述输出结果p-值可以看出回归方程通过回归参数的检验与回归方程的检验，由此得到回归方程 $Y=2.91419+0.0755X$ ，还可以对误差项独立同正态分布的假设进行检验 [3] ，运行结果见图3。

Figure 3. Test result correlation diagram

图3. 检验结果相关图

1) Residual vs Ftted为拟合值对残差的图形，可以看出，数据点都基本均匀地分布在直线y = 0的两侧，无明显趋势；

2) Normal QQ-plot图中数据点分布趋于一条直线，说明残差是服从正态分布的；

3) Scale-Location图显示了标准化残差(standardized residuals)的平方根的分布情况。最高点为残差最大值点；

4) Cook距离(Cook’s distance)图显示了对回归的影响点。

由上面的分析我们得出，一年级学生重修率与低收入家庭学生百分比之间的关系可以用线性方程 $Y=2.91419+0.0755X$ 表示。

4.2. 1994~1995年和2004~2005年学生一年级重修率的差异

由于2.1.2节用单因子方差分析一年级学生重修率，结果显示两年份对这两变量没有较大的差异。于是本小题主要是使用平行回归线模型，d为构造的哑变量：

$Y={\beta }_0+{\beta }_{1}X+{\beta }_{2}d+\epsilon =\{\begin{array}{l}Y={\beta }_0+{\beta }_{1}X+\epsilon ;d=0\\ Y={\beta }_0+{\beta }_{1}X+{\beta }_2+\epsilon ;d=1\end{array}$

在R程序中对两年份一年级学生重修率百分比分析结果如图4：

Figure 4. Two-year first-year student rework rate percentage scatter plot and linear regression line

图4. 两年份一年级学生重修率百分比散点图及线性回归线

图形中三角形的散点代表1994年，加号的散点代表2004年，d = 0为斜率较小的虚拟回归线，即1994年的散点图形虚拟回归： $Y={\beta }_0+{\beta }_{1}X+\epsilon$ ；d = 1为斜率较大的虚拟回归线，即2004年的散点图形虚拟回归： $Y={\beta }_0+d+{\beta }_{1}X+\epsilon$。

在R程序中输出的回归结果：

Call:

lm(formula = y ~ 1+ x + d)

Residuals:

Min 1QMedian 3Q Max

−8.6768 −2.5451−0.47691.6624 11.3469

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 2.84900 0.84995 3.352 0.001076 **

x 0.07248 0.01917 3.782 0.000245 ***

d 0.38311 0.72716 0.527 0.599274

---

Signif. codes:0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.832 on 119 degrees of freedom

Multiple R-squared:0.127, Adjusted R-squared:0.1124

F-statistic: 8.659 on 2 and 119 DF, p-value: 0.0003083

当d = 0，即1994年时， $y=0.07x+2.849$ ；当d = 1，即2004年时， $y=0.07x+3.232$。两模型之间的差异为0.38311，即哑变量系数的估计值。因此，我们得出在1994年和2004年一年级学生重修率百分比的差值约为38%。

4.3. 1994~1995年和2004~2005年一年级学生重修率与低收入家庭学生百分比之间关系的差异

本小题主要采用不相关回归：

$Y={\beta }_0+{\beta }_{2}d+{\beta }_{1}X+{\beta }_{3}dX+\epsilon =\{\begin{array}{l}Y={\beta }_0+{\beta }_{1}X+\epsilon ;d=0\\ Y={\beta }_0+{\beta }_2+\left({\beta }_1+{\beta }_3\right)X+\epsilon ;d=1\end{array}$

在R程序中显示图形，图5中三角形的散点代表1994年，加号的散点代表2004年，d = 0为斜率较小的虚拟回归线，即1994年的散点图形虚拟回归： $Y={\beta }_0+{\beta }_{1}X+\epsilon$ ；d = 1为斜率较大的虚拟回归线，即2004年的散点图形虚拟回归： $Y={\beta }_0+{\beta }_2+\left({\beta }_1+{\beta }_3\right)X+\epsilon$。

Figure 5. Repetition rate of first-year students in two years and percentage scatter plot and linear regression line of low-income students

图5. 两年份一年级学生重修率与低收入家庭学生百分比散点图及线性回归线

对模拟回归线进行分析，R程序运行结果为：

Call:

lm(formula =y ~ 1 + x + d + d * x)

Residuals:

Min 1Q Median 3Q Max

−8.1606 −2.6121 −0.55761.7495 11.6014

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept)3.27194 1.22347 2.6740.00855**

x 0.06080 0.03093 1.9660.05167 .

d −0.389561.76109−0.2210.82532

x:d 0.01903 0.03949 0.4820.63066

---

Signif. codes:0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.845 on 118 degrees of freedom

Multiple R-squared:0.1288, Adjusted R-squared:0.1066

F-statistic: 5.813 on 3 and 118 DF,p-value: 0.0009689

当d = 0即1994年时， $y=0.06x+3.27$ ；当d = 1即2004时， $y=0.07x+2.88$。

从上述的回归方程显示，我们初步认为在1994年和2004年这两年份时，一年级学生重修率和低收入家庭学生百分之间没有较大差异：分析 ${\beta }_1$ ，一个模型的 ${\beta }_1$ 估计值是6%，另一个模型 ${\beta }_1$ 估计值是7%，截距分别为3.27，2.88。为了确保结果的可靠性，我们再一步对模型作偏F检验，在R程序中的结果为：

Analysis of Variance Table

Model 1: y ~ 1 + x

Model 2: y ~ 1 + x + d + d * x

Res. Df RSS Df Sum of Sq F Pr(>F)

1 120 1751.9

2 118 1744.42 7.512 0.2541 0.7761

$\begin{array}{c}F=\frac{\left(RS{S}_{\left(d=0\right)}-RS{S}_{\left(d=1\right)}\right)/\left(D{f}_{\left(d=0\right)}-D{f}_{\left(d=1\right)}\right)}{RS{S}_{\left(d=1\right)}/D{f}_{\left(d=1\right)}}\\ =\frac{\left(1751.9-1744.4\right)/\left(120-118\right)}{1744.4/118}\approx 0.2537\end{array}$

正如预期的结果那样，这两模型没有较大的差异，即年份没有对一年级学生重修率和低收入家庭学生百分比之间的关系产生较大影响。因此，我们宁愿选择重合线模型，而不是不相关的回归线模型。