基于改进多元线性回归分析的雾霾天绝缘子故障诊断研究

Study on Fault Diagnosis of Insulator in Haze Based on Improved Multivariate Linear Regression Analysis

摘要: 本文主要是在模拟雾霾的情形下对绝缘子故障情况进行分析，通过上述实验得到不同情形下产生闪络现象的电流电压数据。进而针对本实验中的特殊性，结合EIV模型的统计学特性，对传统的多元线性回归模型进行一定的改进，使之能更好、更便利地分析各个因变量之间的相互关联性及模型拟合效果，克服了数据稳定性的限制。利用改进后的回归模型，分别建立故障诊断预测模型与小波分析参数区间预测误差模型，进而根据回归分析得到的绝对平均误差和拟合优化检验，结合这两个模型，来判断故障类别，经过对三种不同情形下故障的检验，这两种模型在实际应用中均能够满足要求。

Abstract: The insulator is analyzed under the condition of simulated haze in this paper, and the current and voltage data of the flashover under different conditions are obtained through the above experiments. According to the particularity of the experiment and the statistical characteristics of the Errors in Variables model, the traditional multiple linear regression model has been improved to better and more conveniently analyze the correlation between the various dependent variables and the fitting effect of the model, overcoming the limitation of data stability at the same time. Using the improved regression model, we established the fault diagnosis prediction model and the wavelet analysis parameter interval prediction model respectively, and the fault categories are judged based on the absolute average error and the fitting optimization test obtained by the two models and the regression analysis. After testing, two models can meet the requirements of diagnostic faults and prediction errors.

1. 研究背景

绝缘子通常用于支持母线或电气设备，该特殊控件在输电线路的应用中有着很大的作用。污闪是指绝缘子上附着的灰尘等物形成的污秽层在湿润环境的影响下，使绝缘子能够导电、放电的现象。对于以往的研究，主要针对绝缘子在雨雪等天气中的状态进行分析 [1] [2] ，但近几年来雾霾严重程度持续加剧，其引起的问题也越来越多，因此研究雾霾天气下的绝缘子污闪显得十分必要 [3] [4] 。本文通过使用不同故障模型来预测误差，实现故障检测的目的。

2. 实验研究步骤

我们首先对所需要的绝缘子进行一系列处理实验 [5] ，实验连接线路图如图1所示，具体实验内容和步骤如下：

1) 绝缘子处理：首先用蒸馏水对所用绝缘子进行清洗，保证充分清除其表面原有的污秽层。然后悬挂绝缘子使其阴干，期间注意防止表面遭到二次污染。

2) 污秽物处理：用精度为0.1 mg的光学分析天平称量5份污染物，每份高岭土13,902 mg、NaCl 1390.2 mg。将称量出的NaCl和高岭土放入容器中，加适量的蒸馏水充分搅拌。将搅拌后的污染液均匀地涂刷于绝缘子表面，以模拟重度污秽层，然后悬挂阴干。

3) 雾霾成分准备：根据表1将NaNO₃和Na₂SO₄按照不同比例混合 [6] [7] ，以模拟不同情况下的雾霾场景。

Table 1. Experimental grouping table

表1. 实验分组表

4) 按照图示连接实验线路图，用上述不同成分 [8] 的雾霾分别对形成污秽层的绝缘子加湿，当绝缘子污层表面形成水膜且其湿度达到饱和时，再用均匀升压法进行加压至闪络现象出现。

Figure 1. Experimental wiring diagram

图1. 实验连接线路图

5) 记录出现闪络现象时的电流和电压。

3. 实验数据预处理

我们用min-max normalization法则来对实验测量所得数据进行预处理，其原理是对原始数据进行线性变化，设 $i_{\min }$ 和 $i_{\max }$ 分别为i的最小值和最大值，其转换公式表现为：

$f\left(i\right)=\frac{i-i_{\min }}{i_{\max }-i_{\min }}$ (1)

我们在本次实验中得到了四组实验数据，分别为1组：蒸馏水对照组、2组：低浓度硝酸盐雾霾组、3组：高浓度硝酸盐雾霾组、4组：高浓度硫酸盐雾霾组，部分样本数据如下表2所示。

Table 2. Partial sample data table

表2. 部分样本数据表

4. 实验研究分析方法

4.1. 多元线性回归模型

4.1.1. 模型概念

多元线性回归模型是以多个特征向量作为前提，研究因变量与自变量之间的相关性，从而确立能够体现两者关系的模型，然后依据得到的模型来处理实验数据，并加以预测，多元线性回归方程的矩阵能够体现为：

$y=X\beta +\epsilon$ (3)

$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right],\epsilon =\left[\begin{array}{c}{\epsilon }_0\\ {\epsilon }_1\\ ⋮\\ {\epsilon }_n\end{array}\right],\beta =\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_p\end{array}\right],X=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1p}\\ 1& x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& ⋮& & ⋮\\ 1& x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right]$ (4)

其中， $\left(x_{i1},x_{i2},\cdots ,x_{ip},y_i\right)$ 是n次独立观测值， ${\epsilon }_i\sim N\left(O,{\sigma }^2\right)$ ， $i=1,2,\cdots ,n$ ，且独立同分布，最小二乘估计值 $\hat{\beta }$ 即 $\beta$ 的最小二乘函数。

$Q\left(\beta \right)={\left(Y-X\beta \right)}^{\text{T}}\left(Y-X\beta \right)$ (5)

达到最小的 $\beta$ 值，估计为：

(6)

从而可以得到经验回归方程

$\hat{Y}={\hat{\beta }}_0+{\hat{\beta }}_1{X}_1+\cdots +{\hat{\beta }}_p{X}_p$ (7)

根据实验所得样本数据，我们能够看出：数据具有极强的波动性与不稳定性，在实际应用中因变量与自变量的观测值往往是由其真实值与随机观测误差两部分构成，因此简单地认为线性回归方程中只存在模型固有误差会给最终结果造成较大影响。为了提高模型的精确度，结合Errors in Variables模型，在针对本文中绝缘子进行分析时对所有变量都考虑随机误差，多元线性回归模型 $y=X\beta +\epsilon$ 即变为：

$Y-v=\beta \left(x+u\right)+\epsilon$ (8)

$\begin{array}{l}y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right],\epsilon =\left[\begin{array}{c}{\epsilon }_0\\ {\epsilon }_1\\ ⋮\\ {\epsilon }_n\end{array}\right],\beta =\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_p\end{array}\right],X=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1p}\\ 1& x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& ⋮& & ⋮\\ 1& x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right]\\ Y=\left[\begin{array}{c}{Y}_1\\ Y_2\\ ⋮\\ Y_n\end{array}\right],u=\left[\begin{array}{c}{u}_1\\ u_2\\ ⋮\\ u_n\end{array}\right],v=\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]\end{array}$ (9)

其中， $E\left(u\right)=E\left(v\right)=0$ ， $u,v,x$ 不相关。其经验回归方程随之变为：

$\hat{Y}-\hat{v}={\hat{\beta }}_0+{\hat{\beta }}_1{X}_1+\cdots +{\hat{\beta }}_p{X}_p+\left({\hat{\beta }}_0+{\hat{\beta }}_1+\cdots +{\hat{\beta }}_p\right)\hat{u}$ (10)

4.1.2. 代价函数

我们在确定了模型之后，引入一个代价函数来进一步评价模型的好坏 [9] ，代价函数不单能够评估模型优劣，且可以不断训练模型的参数 $\beta$ ，因此，我们能够获得较小的代价函数的平均值 $J\left(\beta \right)$ 用公式可以表示为：

$J\left({\beta }_i\right)=\frac{1}{2m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\left({\hat{y}}^{\left(i\right)}-y^{\left(i\right)}\right)}^2}=\frac{1}{2m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\left(h_{\beta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2}$ (11)

其中，m代表训练样本数目， $h_{\beta }\left(x^{\left(i\right)}\right)$ 代表用参数 $\beta$ 和x预测的y值， $y^{\left(i\right)}$ 代表原始训练样本的y值，也就是真实值。

4.1.3. 评价标准

由上述确定了模型的相关参数之后，我们需对其进行一定的评价，来确定模型的预测情况，一般常用的评价指标有直接误差、绝对平均误差等，根据本问题的研究需求，我们使用平均误差、绝对平均误差、均方根误差、拟合优度检验来评价模型。相关公式分别为：

1) 平均误差。

$\mu =\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\delta }_i}}{n}$ (12)

其中， $\delta$ 表示模型的误差，即输出值与实际值之差。

2) 绝对平均误差。

${\mu }^{\prime }=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|{\delta }_i\right|}}{n}$ (13)

3) 均方根误差。

$\sigma =\sqrt{\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left({\delta }_i\right)}^2}}{n}}$ (14)

4) 拟合优度检验。

$R^2=\frac{E}{T}=1-\frac{R}{T}$ (15)

$\{\begin{array}{l}T={\displaystyle \sum {\left(Y_i-\bar{Y}\right)}^2}离差平方和\\ R={\displaystyle \sum {\left(Y_i-{\hat{Y}}_i\right)}^2}残差平方和\\ E={\displaystyle \sum {\left({\hat{Y}}_i-\bar{Y}\right)}^2}回归平方和\end{array}$ (16)

4.1.4. 算法简介

在计算模型最优解的过程中，我们一般可将其视为一个迭代过程，以均方根误差为衡量标准，不断地训练数据。

Step1：收集数据样本。

Step2：计算初始的代价函数值。

Step3：以均方根误差为标准，不断改变 ${\beta }_i$ 的值，最终得到代价函数的最小值。

Step4：分别得到不同的预测评价标准值，结合得到的最优的模型参数。

通过MATLAB和SPSS仿真计算和建立多元线性回归模型：

1组：蒸馏水对照组

$Y=0.010683-0.03687x_1-0.00019x_2$

2组：低浓度硝酸盐雾霾组

$Y=-0.00025+0.029613x_1-0.00013x_2$

3组：高浓度硝酸盐雾霾组

$Y=-0.00038+0.019528x_1-0.00013x_2$

4组：高浓度硫酸盐雾霾组

$Y=0.00079-0.02419x_1-0.00067x_2$

4.2. 故障诊断预测模型

得到的不同组别的线性回归模型、结合对应的故障诊断模型进行预测 [10] [11] ，由于平均误差表示的是预测得到的所有随机误差的平均值，拟合优度检验则是用来检验预测值和理论值之间的一致程度，故当评价标准中的平均误差与拟合优度检验值最小时，我们便认为是用最适合该故障的线性回归模型来对其进行诊断预测的，不同模型预测参数如表3所示，综上述，故障诊断预测的方法可大抵描述为：

Step1：利用待判别故障的数据求得线性回归模型，以及对应的平均误差和拟合优度检验等评价标准；

Step2：利用最小信息准则Akaike information criterion，对多种模型进行选择和判别；

Step3：以绝对平均误差与拟合优度检验值为标准，前者值最小且后者值最大的即认为是待判别故障的故障类型。

Table 3. Prediction parameters of different models

表3. 不同模型预测参数

4.3. 小波分析参数区间预测模型

绝缘子在发生闪络现象时产生的电流和闪络电压会随着故障类别而不同，然而数据的复杂性导致我们无法直接获取这之间的联系，我们借用小波分析法，通过伸缩与平移多种运算功能，从所得函数中提取有效信息，进行多尺度细化分析得出故障类别。之后通过小波分析法得到不同故障类别的高频信号，当故障的类别变化时，其参数区间也有所不同，由此可以通过待判别故障的参数所在的参数区间，来判断其对应的故障类别。

小波分析法是一种时域与频域的局部变换的信号分析方法，也是一种克服其他信号处理技术缺陷的独特方法，具体表现为低频区域时：高频分辨率且低时间分辨率、高频区域时：低频分辨率且高时间分辨率。设 $\psi \left(t\right)\in L^2\left(R\right)$ ，其中 $L^2\left(R\right)$ 代表实数空间信号，当 $\hat{\psi }\left(\omega \right)$ 满足容许条件时，有：

$C_{\psi }={\displaystyle \underset{R}{\int }\frac{{\left|\hat{\psi }\left(\omega \right)\right|}^2}{\left|\omega \right|}\text{d}\omega }<\infty$ (17)

$\hat{\psi }\left(\omega \right)=\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^{+\infty }\psi \left(\omega \right){\text{e}}^{-i\omega t}\text{d}t}$ (18)

对于连续信号 $f\left(t\right)$ 的连续小波变换，即Continue Wavelet Transform，可以表现为：

$W_{\psi }f\left(a,b\right)=\frac{1}{\sqrt{a}}{\displaystyle \underset{R}{\int }f\left(t\right)\bar{\psi }\left(\frac{t-b}{a}\right)\text{d}t}$ (19)

其中a代表尺度对应于频率，可将小波伸缩变换；b代表平移量对应于时间，可将小波位移变换，然而实际应用中，我们一般分析小波的离散变换，令 $a=a_0^m$ ， $b=n{b}_0{a}_0^m$ ， $m,n\in R$ ，有：

$W_{\psi }f\left(m,n\right)=a_0^{-\frac{1}{2}m}{\displaystyle {\int }_{-\infty }^{+\infty }f\left(t\right)\bar{\psi }\left(a_0^{-m}t-n{b}_0\right)\text{d}t}$ (20)

关于小波分析的多层分解，其结构图大致表现如下图2所示。

Figure 2. Multi-layer wavelet decomposition diagram

图2. 小波多层分解图

对于信号 $f\left(t\right)\in L^2\left(R\right)$ ，其分解公式可以写作：

$f\left(t\right)={\displaystyle \underset{i}{\overset{I}{\sum }}{s}_{ij}{\varphi }_{ij}\left(t\right)}+{\displaystyle \underset{i}{\overset{I}{\sum }}{\displaystyle \underset{j}{\overset{J}{\sum }}{d}_{ij}{\psi }_{ij}\left(t\right)}}$ (21)

$s_{i,j+1}={\displaystyle \underset{m}{\overset{M}{\sum }}S\left(m-2j\right)s_{ij}}$ (22)

$d_{i,j+1}={\displaystyle \underset{m}{\overset{M}{\sum }}D\left(m-2j\right)s_{ij}}$ (23)

其中 ${\varphi }_{ij}\left(t\right)$ 代表尺度函数，i表示其分解程度，j表示其离散程度， $S\left(j\right)$ 、 $D\left(j\right)$ 分别表示低通滤波与高通滤波。

由上述方法得到的多元线性回归模型的绝对平均误差，结合小波分析法 [12] ，迭代计算出各层的参数最大值和最小值，即得到不同故障的参数区间，如表4和图3所示。

Table 4. Parameter intervals of different faults

表4. 不同故障的参数区间

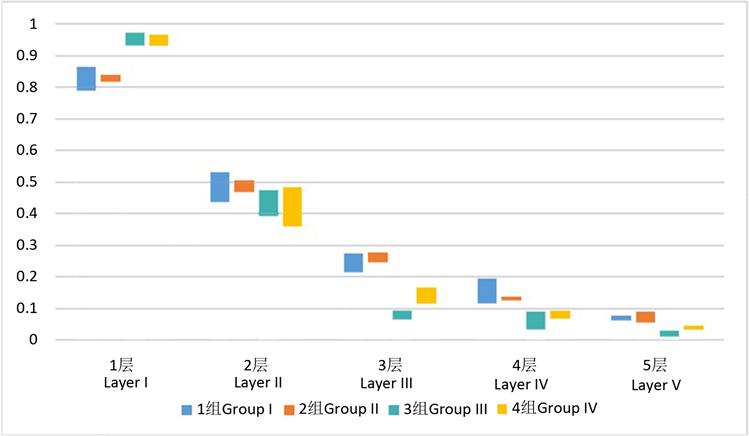
Figure 3. Column diagram of parameter interval for different faults

图3. 不同故障的参数区间柱形图

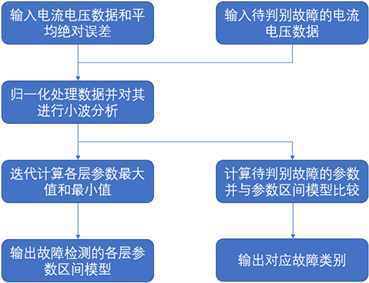
Figure 4. Flow chart of wavelet analysis parameter interval prediction model

图4. 小波分析参数区间预测模型流程图

根据图4所示的模型流程图，进一步分析参数区间的图表可以发现，不同类别的故障在2层时参数结果较为接近，在接下来判断类别时我们可以将其看作是否会发生闪络现象的依据，其余层数则看作类别判断的依据；1组对照组和2组低浓度硝酸盐组所得结果较为接近，即参数区间重合部分较多，分析原因可能是由于模拟雾霾成分较为接近。

5. 实验结果分析

为了检验我们建立的模型的可靠程度，将三种待判别故障的数据分别输入故障诊断预测模型和小波分析参数区间预测误差模型，可得到如下表5至表7的结果：

1) 故障诊断预测模型

利用上述建立的故障预测模型分别检验三种待判别故障。

Table 5. Prediction and evaluation criteria of fault 1

表5. 故障一的预测评价标准

Table 6. Prediction and evaluation criteria of fault 2

表6. 故障二的预测评价标准

Table 7. Prediction and evaluation criteria of fault 3

表7. 故障三的预测评价标准

Table 8. Test results show the table

表8. 检验结果显示表

通过上述得到的数据分析，故障一中的平均误差最小与拟合优度检验最大时对应的是3组模型，即判别为高浓度硝酸盐故障；故障二中的平均误差最小与拟合优度检验最大时对应的是2组模型，即判别为低浓度硝酸盐故障；故障三中的平均误差最小与拟合优度检验最大时对应的是4组模型，即判别为高浓度硫酸盐故障。由表格所示，代入模型所得出的故障与实际吻合，表明该模型能够较好的判断出雾霾天绝缘子的故障类型，可总结为表8所示。

2) 小波分析参数区间预测误差模型

将已有三种待判别故障代入参数区间进行检测，结果如表9所示。

Table 9. Parameter interval prediction failure table

表9. 参数区间预测故障表

由计算出的三种故障的各层参数值与故障类别的参数区间对照，所得结果与实际相吻合，表明该模型能够较好得利用小波分析与绝对平均误差来判断故障类别，准确度基本满足需求。同时证明该模型对于分析故障有着一定的通用性，对待不同情形，都能有不错的预测效果。

6. 结束语

本文首先通过建立多元线性回归模型 [13] [14] 分析不同情形下的电流电压数据，然后分别建立故障诊断预测模型和小波分析参数区间预测误差模型来判别故障的类别。其中采用的回归分析法便于处理多个因变量影响的问题，且能够较为准确的计算各个因变量之间的相互关系与模型拟合优度，相比于时间序列等预测方法来说，不受数据稳定性的限制，然而其中也存在忽略交互效应和非线性联系的可能性。