基于Levenberg-Marquardt算法的心电高斯模型研究

Levenberg-Marquardt Algorithm-Based Gaussian Model Research for ECG

摘要: 针对心电信号中各构成成分(P波、QRS波、T波)波形特征，本研究提出了一种基于伯格–马夸尔特算法创建心电高斯模型以实现心电波形特征研究进而对心电特征进行定性评价研究。首先，基于小波分解对心电信号进行预处理，以消除基线漂移以及背景噪声；其次，以心电信号各R峰间距为参考，按照1:2的分割比例对心电信号进行周期分割；最后，基于Levenberg-Marquardt (LM)算法创建心电高斯混合模型以刻画各成分波形特征。本算法通过对MIT-BIH心律失常数据库中48条心电数据进行分析，利用其拟合优度均值为0.9668对本算法可行性进行了验证。

Abstract: Aimed at the waveform characteristics of main components (P wave, QRS complex and T wave) to an electrocardiogram (ECG), this study proposes a novel method based on Levenberg-Marquardt algorithm (LMA) to build the Gaussian model for researching ECG signal, and then to character the features of each component. Firstly, the wavelet decomposition-based preprocessing method is employed to cancel baseline shift and background noise existing in ECG signal. Secondly, ECG signal is segmented into periodic signal based on the distance between tow sequence R peaks as well its ratio of 1:2. Finally, LMA-based Gaussian Mixture model is built to character each component waveform. The performance of the proposed method has been evaluated by using the 48 ECG records of MIT-BIH arrhythmia database, and the higher average of R-square value 0.9668, used to measure the goodness of fit, has been achieved.

1. 引言

近年来心血管疾病的患病率和死亡率均呈现持续增长的趋势，并且心血管疾病死亡人数连续多年位居疾病死亡之首。根据《中国心血管报告2018》 [1]，2016年农村因心血管疾病死亡人数占全部因疾病死亡人数的45.50% (见图1(a))，城市因心血管疾病死亡人数占全部死亡人数的43.16% (见图1(b))。依据心血管疾病患病率持续上升的趋势，推测我国现有2.9亿患者，其中心脏病占有很大比重。我国心血管病防治工作面临严峻挑战。

Figure 1. The main cause of death in rural and urban residents in China in 2016

图1. 2016年中国农村和城市居民主要疾病死因构成

传统心血管疾病治疗最大弊端是需持续长时间心电信号记录，从而导致绝大多数心血管疾病患者错过了最佳理疗期。随着计算机技术，数字信号处理手段等先进技术的不断发展，借助计算机和数字信号处理手段对心电图信号进行检测、处理和分析已逐步取代传统诊断方式。心电图(ECG)包含大量用于分析心脏功能的生理信号，是用来诊断心脏疾病的主要依据之一。表征心电信号的形态特征是诊断心脏性疾病、心率变异性分析、生物统计学和心电信号自动分类中最重要的步骤，这些系统的性能很大程度上依赖于心电信号描述的准确度。而心电信号的特征提取、识别及分类已经被国内外研究人员引入了许多种算法。一般可用的特征表示方法包括形态学 [2] 、时间信息 [3] 、小波变换 [4] 、高阶统计量(HOS) [5] 、Hermite基函数 [6] 、ECG波间隔 [7] 、选定的采样点 [8] 、QRS波段镜像高斯模型 [9] 等。

心电信号特征提取经历了从单个节拍特征提取到海量心电信号特征提取的发展过程。基于滤波技术和决策规则的方法计算效率高，是任何心电分析的理想方法。一般来说，预处理阶段采用各种信号处理技术来增强心电波的特征和抑制噪声，但大多数方法都存在一定的缺点。如，基于小波变换的预处理存在母波和尺度的选择问题，基于基准点描述特征存在难度较大和精度较低的问题。对于真实的心电信号波形形态各异，单一的决策规则很难描述各种病理信号。周群一将QRS复合波建立数学模型并应用在心拍的分类，但该方法只描述了QRS复合波的形状，却丢失了其他部分信息。

本文提出了一种基于简单的小波变换和Levenberg-Marquardt算法建立函数模型表述心电节拍信号形态的方法。本文结构组织如下。第一部分讲述基于小波分解对心电信号进行简单的预处理——去除基线漂移以及背景噪声，第二部分介绍了以心电信号各R峰间距为参考，按照1:2的分割比例对心电信号进行周期分割，第三部分详细介绍了建立数学模型的两个步骤。最后给出了实验结果。使用MIT-BIH 心律失常数据库对本文提出的方法进行了实验评估。

2. 方法

根据算法实现原理，心电信号高斯模型拟合主要分为三部分如图2。

Figure 2. Block diagram of Gaussian fitting of ECG signals

图2. 心电信号高斯拟合流程框图

2.1. 小波变换处理

在信号处理中，傅里叶变换在处理非平稳信号及刻画信号在时域中的局部特性上具有局限性。由此衍生出了小波变换。小波分解采用有限时间分布且衰减的函数作为基，使得小波变换具有了傅里叶变换没有的时频分析能力，其原理如公式(1)所示。

$C_{\phi }={\displaystyle {\int }_{-\infty }^{+\infty }\frac{{\left|\hat{\phi }\left(w\right)\right|}^2}{\left|w\right|}\text{d}\omega }<+\infty$ (1)

小波变化广泛应用在信号处理、数字图像处理。为了实现很好的处理效果，在实际应用中，学者在傅里叶变换基础上衍生出许多小波，其中dB小波具有正交性、指数多项式消失距和连续紧支性等特性，因此本研究采用Daubechies小波作为母小波进行小波变换。研究 [10] 表明心电信号基线频率段为0.15~0.3 Hz，鉴于此本研究根据心电信号特征选用dB8小波对心电信号处理，心电信号原始波形如图3所示，其去除基线漂移效果如图4所示。

2.2. 心电信号的切割

第二步中，算法通过定义一组规则来识别和定位感兴趣的点。如R峰峰值位置、P波起始点、T波终点等。在MIT-BIH心电信号数据库中，每组数据都经过两位心电图专家独立对信号进行标注，标注内容包括信号质量、节律变化、节拍局部说明及每个心电节拍的类型。其中每个心电节拍的类型都准确地标注在该节拍的R波波峰位置，方便了广大研究人员进行研究分析。本文就以注释位置为标准，每个RR间隔的2:1划分每个心电节拍 [11]，避免心律不齐信号切分的完整性，保证了切割后的心电节拍中都包含有P波、QRS复合波和T波等主要波形。对心电波形图(图5)心拍分割处理的两个阶段及实验结果如图6，图7所示。该切割方法在心律失常的情况下依然可以按要求将心电节拍切割。

Figure 3. Original waveform of the ECG signal

图3. 心电信号原始波形图

Figure 4. ECG signal removal baseline drift plot

图4. 心电信号去除基线漂移图

2.3. 建立高斯模型

高斯函数可用式(2)表示，式中 $y_0$ 为峰高， $\mu$ 为峰的中心， $\sigma$ 为高斯曲线的峰宽。高斯函数是非线性函数，对公式(3)取对数将其线性化，最终得式(4)线性函数表达式

$y=y_0{\text{e}}^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}$ (2)

(3)

$\ln y=\ln y_0-\frac{{\mu }^2}{2{\sigma }^2}+\frac{2\mu x}{2{\sigma }^2}-\frac{x^2}{2{\sigma }^2}$ (4)

将函数系数分别计为出 $c_1,c_2,c_3$，则

$c_1=\ln y_0-\frac{{\mu }^2}{2{\sigma }^2},c_2=\frac{\mu }{{\sigma }^2},c_3=-\frac{1}{2{\sigma }^2}$ (5)

Figure 5. Original waveform of the ECG signal

图5. 心电信号原波形图

Figure 6. ECG signal R peak location map

图6. 心电信号R峰定位图

Figure 7. ECG signal segmentation

图7. 心电信号分割图

公式(4)可以表示为 $\ln y=\left[\begin{array}{ccc}1& x& x^2\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ c_3\end{array}\right]$，对于单高斯函数拟合，可以计为 $Y=A_{1\times 3}{C}_{3\times 1}$

对于多高斯函数公式(6)所示

$f\left(y,n\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}{y}_m\frac{1}{\sqrt{2\pi }{\sigma }_m}{\text{e}}^{-\frac{{\left(x-{\mu }_m\right)}^2}{2{\sigma }_m^2}}}$ (6)

其y为长度为n，对应的公式(4)可以表示为

$\left[\begin{array}{c}\ln y_1\\ ⋮\\ \ln y_n\end{array}\right]=\left[\begin{array}{ccc}1& x_1& x_1^2\\ ⋮& \ddots & ⋮\\ 1& x_n& x_n^2\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ c_3\end{array}\right]$ (7)

简记为 $Y_n=A_{n\times 3}{C}_{3\times 1}$,计算可得 $C={\left(A^{\text{T}}A\right)}^{-1}{A}^{\text{T}}Y$。数组C中都可以由参数 $y_0,\mu ,\sigma$ 计算出来。但由于多峰的复杂性， $y_0,\mu ,\sigma$ 只是估计值因此要采用最小二乘 [12] 拟合求出最优的高斯函数参数。高斯函数拟合转化为了非线性最小二乘问题，最小二乘问题可分为线性和非线性两类。线性最小二乘问题的解是封闭式的确定性的，即 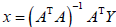。对于非线性最小二乘问题通常采用迭代法求解，在计算中，有许多优化算法用于处理最小二乘问题，使用较少的计算量达到很好的结果。比如梯度下降算法、高斯–牛顿算法、共轭梯度法、列为伯格–马夸尔特算法和信赖域算法等。心电信号的高斯拟合是非线性的最小二乘问题，目标函数可以表示为

$F\left(x\right)={\displaystyle \underset{i=1}{\overset{m}{\sum }}{f}_i^2\left(x\right)}$ (8)

其中 $x={\left(x_1,x_2,x_3,\cdots ,x_n\right)}^{\text{T}}$，通过优化使 $F\left(x\right)$ 最小化，本实验选用了在曲线拟合中应用广泛的列为伯格–马夸尔特算法和信赖域算法进行实验并对比二者结果。

2.3.1. 列为伯格–马夸尔特算法

列为伯格–马夸尔特算法(简称LMA或LM)，也称为阻尼最小二乘(DLS)。它是建立在高斯牛顿算法和梯度下降算法之间的优化算法，在许多情况下，即使初始值距离最终的最小值很远，它也可以找到解决方案。LM算法是解决非线性最小二乘问题的重要算法，主要应用于曲线拟合问题。LM算法流程如下：把目标函数式(8)在 $x^k$ 处一阶泰勒展开，用 ${\varphi }_i\left(x\right)$ 表示可

(9)

则

$\begin{array}{l}\psi \left(x\right)={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\varphi }_i^2\left(x\right)}\\ ={\left(\left[\begin{array}{c}\nabla f_1{\left(x^k\right)}^{\text{T}}\\ ⋮\\ \nabla f_m{\left(x^k\right)}^{\text{T}}\end{array}\right]x+\left[\begin{array}{c}\nabla f_1{\left(x^k\right)}^{\text{T}}{x}^k-f_1\left(x^k\right)\\ ⋮\\ \nabla f_m{\left(x^k\right)}^{\text{T}}{x}^k-f_m\left(x^k\right)\end{array}\right]\right)}^{\text{T}}\left(\left[\begin{array}{c}\nabla f_1{\left(x^k\right)}^{\text{T}}\\ ⋮\\ \nabla f_m{\left(x^k\right)}^{\text{T}}\end{array}\right]x+\left[\begin{array}{c}\nabla f_1{\left(x^k\right)}^{\text{T}}{x}^k-f_1\left(x^k\right)\\ ⋮\\ \nabla f_m{\left(x^k\right)}^{\text{T}}{x}^k-f_{im}\left(x^k\right)\end{array}\right]\right)\end{array}$ (10)

用 $\psi \left(x\right)$ 近似表示进每一步迭代。

令 $A_k=\left[\begin{array}{c}\nabla f_1{\left(x^k\right)}^{\text{T}}\\ ⋮\\ \nabla f_m{\left(x^k\right)}^{\text{T}}\end{array}\right]$， $B=\left[\begin{array}{c}\nabla f_1{\left(x^k\right)}^{\text{T}}{x}^k-f_1\left(x^k\right)\\ ⋮\\ \nabla f_m{\left(x^k\right)}^{\text{T}}{x}^k-f_{im}\left(x^k\right)\end{array}\right]$， $f_k=\left[\begin{array}{c}{f}_1\left(x^k\right)\\ ⋮\\ f_m\left(x^k\right)\end{array}\right]$。式(10)可以用式(11)表示

$\psi \left(x\right)={\left(A_{k}x-B\right)}^{\text{T}}\left(A_{k}x-B\right)$ (11)

求导并令导数为零 $A_k^{\text{T}}{A}_{k}x=A_k^{\text{T}}\left(A_k{x}^k-f_k\right)$，将一个正定对角矩阵加入到 $A_k^{\text{T}}{A}_k$ 中，步进增量式变为下面形式 $x-x^k=-{\left(A_k^{\text{T}}{A}_k+\lambda I\right)}^{-1}{A}_k^{\text{T}}{f}_k$。其中I是一个单位矩阵， $\lambda$ 是一个正实数，当 $\lambda =0$ 时，LM算法即为高斯牛顿算法。当 $\lambda$ 很大时， $x-x^k\approx -A_k^{\text{T}}{f}_k$，LM算法就变成了梯度下降算法。的值会在优化中不断变化，控制着x的前进方向，也控制着x每次变化的量。在优化前期类似梯度下降算法使x快速收敛到极值点附近；在优化后期类似高斯牛顿算法，x变化速度逐渐变小，使x稳定收敛达到最优，LM算法在每次迭代中不仅要和高斯牛顿算法一样更新m个函数 $f_i\left(x^k\right)$ 的函数值和一阶偏导数，还要更新 $\lambda$。

2.3.2. 置信域算法

置信域算法(Trust-region methods) [13]，它于1970年由Powell提出。该方法从给定初始解出发，迭代计算，直至达到满意的结果为止。对于 $f\left(x\right)$ 是在 $R^n$ 上的二阶连续可微函数，定义现在点的邻域 ${\Omega }_k$

${\Omega }_k=\left\{x\in R^n|\Vert x-x_k\Vert \le {\Delta }_k\right\}$ (12)

在式(12)中， ${\Delta }_k$ 为置信域半径，在这个邻域中极小化目标函数的近似二次模型，得到近似极小点 $S_k$，其中 。置信域方法的子模问题是

(13)

其中， $s=x-x_k$， $g_k=\nabla f\left(x_k\right)$， $B_k$ 是一个对称矩阵。 ${\Delta }_k$ 根据 $q^{\left(k\right)}\left(s\right)$ 对目标函数 $f\left(x\right)$ 的拟合程度来调整置信域，对于 $S_k$，定于以下两个参量

$Are{d}_k=f\left(x_k\right)-f\left(x_k+s_k\right),Pre{d}_k=q^{\left(k\right)}\left(0\right)-q^{\left(k\right)}\left(s_k\right),r_k=\frac{Are{d}_k}{Pre{d}_k}$ (14)

其中 $Are{d}_k$ 为目标函数下降量为实际下降量， Pred_k 为函数模型的下降量记为预测下降量。 $r_k$ 用来衡量目标函数与实际函数的一致性程度。计算步骤如下：

1) 给出初始值 $x_0$,置信域半径 $\bar{\Delta }$，， $\epsilon \ge 0$，， $0<{\gamma }_1<1$，

2) 如果 $\Vert g_k\Vert \le \epsilon$，则停止计算。

3) 求模型子问题，得到 $S_k$

4) 计算 $f\left(x_k+s_k\right)$ 和 $r_k$ 其中

$x_{k+1}=\{\begin{array}{l}{x}_k+s_k,r_k\ge {\eta }_1\\ x_k,r_k<{\eta }_1\end{array}$ (15)

5) 按照下列规则校正置信域半径，

${\Delta }_{k+1}\in \left[0,{\gamma }_1{\Delta }_k\right],r_k<{\eta }_1$ (16)

${\Delta }_{k+1}\in \left[{\gamma }_1{\Delta }_k,{\Delta }_k\right],r_k\in \left[{\eta }_1,{\eta }_2\right)$ (17)

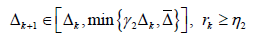(18)

6) 得出 B_k+1，修正 $q^{\left(k\right)},k=k+1$，循环第2步。

3. 实验与分析

3.1. 拟合评价标准

为了确定拟合模型对实际的心电数据是否具有良好的逼近性，采用了误差均方根(RMSE)、误差平方和(SSE)、总平方和(SST)和确定系数(R-square)等拟合优度统计方法。计算方法如下：

$\text{SSE}={\displaystyle {\sum }_k^n{\left(f\left(x_k\right)-y_k\right)}^2},\text{SST}={\displaystyle {\sum }_k^n{\left(f\left(x_k\right)-\frac{1}{n}{\displaystyle {\sum }_k^{n}f\left(x_k\right)}\right)}^2},\text{R-square}=1-\frac{\text{SSE}}{\text{SST}}$ (19)

其中SSE统计参数计算的是拟合数据与原始数据对应点的误差的平方和，其越接近于0，说明模型选择和拟合的结果越好，RMSE和SSE效果一样，这两个参数都表现在拟合结果和原始数据点与点层面的结果。R-square是通过数据整体的变化来描述一个拟合结果的好坏。确定系数越接近1，说明拟合结果对原始数据的解释能力越强。在研究中使用SSE与R-square作为拟合结果的评价指标。

Figure 8. Goodness of fit between LM algorithm and TR algorithm

图8. LM算法与TR算法拟合优度

3.2. 实验结果

本研究采用MIT-BIH心律失常数据库对提出的心电信号拟合方法进行了评价。它包含48小时的两个通道心电记录采样在360赫兹。提出的算法在2.5 GHz Intel(R) Core(TM) i5-5200U CPU上使用MATLAB 2018b实现，并使用数据库中第一通道采集的心电信号进行测试。

根据心电信形态，采用不同的高斯个数为模型，在本研究中，对比了三到七个高斯函数模型对心电节拍拟合的效果。以10,000组心电节验证了多高斯拟合结果，确定以6个高斯函数作为本研究的拟合模型。并采用置信域方法与列为伯格–马夸尔特算法对比了SSE与R-square。两种方法拟合优度对比如图8示，LM算法普遍优于TR算法。