1. 引言
百度上是这么说的:“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”用数学语言表示,即“将平面任意地细分为不相重叠的区域,每一个区域总可以用1,2,3,4这四个数字之一来标记,而不会使相邻的两个区域得到相同的数字。”目前只有通过计算机经过百亿次计算得以证明,还没有可信服的书面证明方式,下面我们来尝试书面证明。
2. 证明思路
2.1. 证明范围及限制条件
平面或球面地图,不考虑“飞地”。
2.2. 思路
根据坎泊关于四色猜测的证明,地图可以认为是无割边的3-正则平面图,其对偶图是一个极大图,泰特猜想认为证明3-正则平面图线的3着色等价于极大图顶点的4着色 [1] 。所以我下面的证明分为两个步骤,第一证明3-正则平面图线的3着色与极大图点的4着色等价,第二证明3-正则平面图线的3着色是必然可以的。
我们不再讨论前人的各种各样的图,现在把所有极大图归为一个图集,把所有3-正则平面图归为一个图集,那么意味着下面的证明只能从这两个图集各自存在的普遍性质及两集之间的固有联系出发来展开论述。
2.3. 证明步骤
步骤一:证明3-正则平面图线的3着色与极大图点的4着色等价。
步骤二:证明3-正则平面图线的3着色是必然可以的。
3. 证明步骤一
3.1. 找出任意3-正则平面图及其对偶图(极大图)之间的点、线、面之间的对应关系
以任意一个极大图为例,我们设此极大图顶点个数为V (V为大于2的自然数),线数为Y,图中三边形(边可能是曲线,后文不再解释)个数为X,由于要证明球面的情况,所以我们认为图外部也是一个三边形,那么三者之间存在如下关系:
Y = 3V − 6,此式可以说是定理,证明也很简单,不再解释;
X = 2Y/3,因为每个三边形需要三根线,每根线均为2个三边形共用;
X = 2V −4,由以上两式推出,显然X必是一个大于等于2的偶数。
我们继续以任意一个3—正则平面图为例,设3-正则图的顶点(三界点)个数为x,线数为y,那么两者之间会有如下关系:
x = 2y/3,每个顶点都通过3根线连接其它顶点,每根线连接2个顶点。
那么我们看对于任意一个固定的3-正则图与其对偶图(极大图)之间存在的必然联系,把3-正则图每一个面浓缩为1个顶点,用线代替面与面之间的邻接关系,即可得到其对偶图。在3-正则图里2个相邻面之间只可能存在1根共线(边),其对偶图里2个相邻顶点之间也只存在一根邻接线,所以此两图线数是相等的并且存在一一对应关系,也就是Y = y = 3V − 6。
另外,3-正则图里的每个顶点也都为3个面所共有,所以在转换成其对偶图的过程中,每个顶点(三界点)都必然化为极大图内的一个三边形,也就是说3-正则图内的每个顶点与其对偶图内的三边形存在一一对应关系,即x = X = 2V − 4,为偶数。
3.2. 根据点、线、面之间的对应关系,以简单图为例找出染色对应规律
根据以上对应关系,如果我们能够对3-正则平面图线进行3色区分,那么3-正则图内的每个顶点所连接的线必然包含3色,然后把每根线的染色一一对应到其对偶图中,也必然导致此对偶图(极大图)中所有三边形的边线包含3色。如图1:
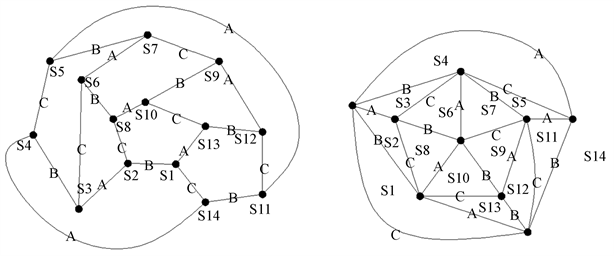
Figure 1. Correspondence between simple 3-regular graphs and their dual graphs
图1. 简单3-正则图与其对偶图的对应关系
图1中左图为3-正则图,右图为其对偶图,3-正则图的顶点与其对偶图的三边形存在一一对应关系,我用s1、s2……sn标注,A、B、C代表3种颜色,对左图线3着色并一一对应到右图,右图中每个三边形的边线均为3色。把图1右图中同一色线加粗,如下图2:
从图2中我们很容易发现,只需要任选一图把同一根加粗线上的顶点交互染A、B两色,另一个根加粗线上的顶点交互染C、D两色,即可完成对此极大图的顶点4染色。
3.3. 以更复杂的图为例,验证染色规律
我们直接引入更复杂的极大图,对所有三边形的边进行3染色,并分别对同一色线加粗,如下图3~5:
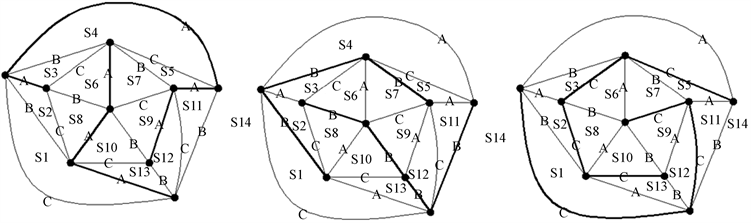
Figure 2. Coarsening of the same color line
图2. 对同一色线加粗处理

Figure 3. Roughening and classification of complex maximum graph A chromatic lines
图3. 复杂极大图A色线加粗并分类
仔细观察以上3图,我们可以把图中同一色线的加粗线归为两类,两类线之间存在另外2色的连接线,而同一类之间不存在连接线,因此我们依然可以一类线的顶点交替染A、B两色,另一类线交替染C、D两色,从而实现极大图的顶点染4色。
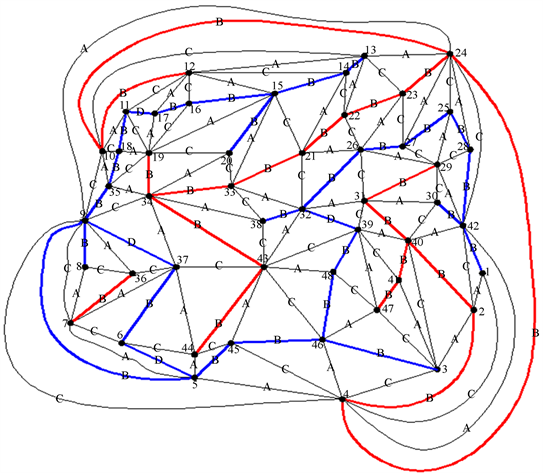
Figure 4. Roughening and classification of complex maximum graph B chromatic lines
图4. 复杂极大图B色线加粗并分类
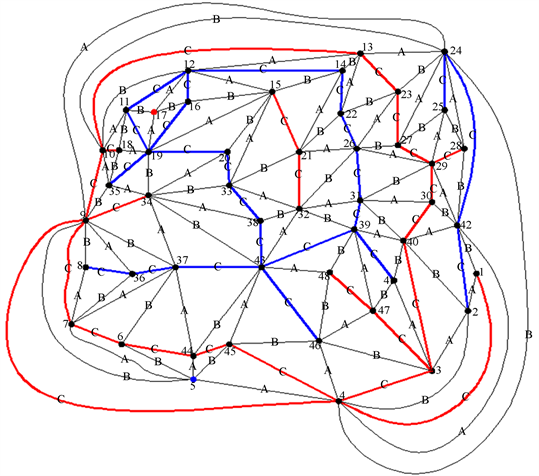
Figure 5. Roughening and classification of complex maximum graph C chromatic lines
图5. 复杂极大图C色线加粗并分类
3.4. 证明3-正则平面图线的3着色与极大图点的4着色等价
以上我们仅证明了3-正则图与其对偶图(也就是极大图)线的一一对应关系,以及如果可以对3-正则图线3染色,即可对其对偶图(极大图)中每个三边形的三边3染色。至于极大图同一色线加粗后可对其顶点4染色,只是我们发现的规律,下面我们来继续证明其必然性。
我们先引入一个定义,我称为两色可染连续线。
两色可染连续线:任意数量点、线连接构成的一条连续线,如果此线的顶点两色可区分,我们称为一条两色可染连续线。
如图6所示,两色可染连续线具备以下几点性质:
a、可以是点、线、环线、树状线及其组合组成;
b、必须是连续的,除了一个点的特殊情况外,可以从任意一个点出发经过不重复路径到达另外一个任意点;
c、环线必须是偶数环,不可存在任何形式的奇数环。
d、如果设点数为v,连线数为y,则y大于或等于v − 1,环越多,点数与线数差值越大。
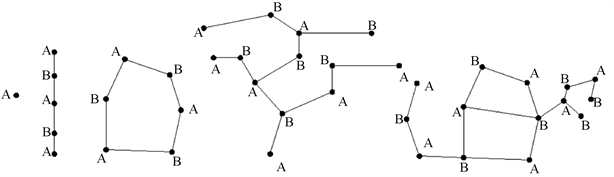
Figure 6. Two-color dyeable continuous line
图6. 两色可染连续线
以上图2~5,各图加粗线每一条都是两色可染连续线,但所有极大图中的线按照我们给定规则3染色,是不是同一色线中的任意一条线都是两色可染连续线?我们只需要证明最重要的一点,那就是没有奇数环。
如图7给出一个A色线的奇数环,并且把此图连接至极大图。

Figure 7. The odd number ring of A-color line
图7. A色线的奇数环
我们上文已经提到,对于一个极大图来说,如果极大图外部也认为是一个三边形,那么三边形个数X = 2V − 4是一个偶数,图7奇数环外可以看做有3个三边形(放球面上会更加明白),是一个奇数,所以奇数环内部三边形个数也必然是一个奇数;又因为每增加1个顶点都必然增加2个三边形,如果增加的这个顶点不在奇数环上,那么增加的两个三边形只能同时在环内或者环外,所以会得到一个推论:当一个极大图被一个奇数环分为内外两部分时,不管存在多少顶点,环内外分别存在的三边形个数都必将是一个奇数;同理被偶数环分为两部分时,环内外三边形的个数都必将是一个偶数。
按照我们前文对线的染色方法可知,任何一色的线数我们需要X/2,也就是说环内B、C两色所染的线数之和与环内三边形个数相等,那么当环内三边形个数X为奇数时必然造成B、C两色的线数不等,所以至少会有一个三边形边线只有两色,如图7中4-5-8三边形。
因此,当我们对一个极大图中所有三边形的边线都用A、B、C三色染色完毕时,同一色线所构成的环必将不会出现奇数环,只能是偶数环。所以,可以确定给定任意极大图,如果对极大图内所有三边形边线进行3色区分,那么同一色线构成的每条连续线均为两色可染连续线。
还有一点要说明,我们上文说两色连续线的点、线关系,同一根两色可染连续线连线数y大于或等于点v − 1,也就是说y最小值是v − 1,而极大图我们染色后同一色线的数量Ya = Y/3 = V − 2,如此则在一个我们给线染色后的极大图中至少会存在两条不连通的同一色线的两色可染连续线,如此才能满足两色可染连续线的点、线关系。
虽然有了两色可染连续线,但要实现极大图顶点4色可染,还要解决另外一个问题,那就是会不会存在三条两色可染连续线循环连接问题?所谓循环连接,就是一条A、B染色的连续线同时与两条C、D染色连续线存在连接线,而两条C、D染色连续线之间同样存在连接线。事实证明这是不可能的,看下图8:
其实这个问题和上个问题原因雷同,如图8(左)所示,如果循环连接,一定会形成像1-2-3一样的边线仅有两色的三边形,如果边线改成三色,如图8(右)则上下两条连续线会连接成一条,在我们染色后的极大图中根本不会出现。
也就是说,如果我们从内到外给两色可染连续线排序,那么只能是按顺序1号线连2号线、2号线连3号线,3号线连4号线,以此类推。对于任意一个n号线,他只能连接n − 1与n + 1号线,而绝不可能越过相邻的两条线与其它两色可染连续线连接,这是一种“平行”关系。因此,我们按照两色可染连续线的排序,如果奇数号线顶点染A、B两色,那么偶数号线顶点我们就染C、D两色,极大图的顶点就必然4色可区分。
要注意的一点是,在及其复杂的极大图中,同一根两色可染连续线上的多个偶数环会包围多条两色可染连续线,因此我们同一个编号的线也会存在多条。
综上所述,如果能实现3-正则平面图线的3着色,那么必然可以实现极大图顶点的4着色,这是完全等价的。
4. 证明步骤二
4.1. 证明思路
下面我们继续来证明任意3-正则平面图线的3着色。上文我们已经完成了第一步的证明,而这第二步的证明更为重要也更为困难。曾经泰特就是因为第二步错误认为所有3-正则图都存在哈密顿圈而错过了四色猜想的书面证明,我在这个问题上用了一年的时间,想了几十种方法,下面我来介绍我自己认为最可靠的一种方法,我称为偶数环消除法。
我的思路是这样的,对于任意一个无割边3-正则图,如果我们能找到同一类型的一种单元,这个单元是3色可染的,另外增加或者减少一个这样的单元都依然会形成3-正则图,且不影响原有3-正则图线的染色,那么对于任意3-正则图来说在不断减去这样一种单元的情况下就会得到顶点比较少的3-正则图,例如x = 4、6等,而这些顶点比较少的3-正则图都已经证明了是3色可染的,我们再用这些顶点比较少的3-正则图一步一步加上我们减少的每个单元,原路返回,并且一步一染色,即可得到任意无割边3-正则图线的3染色。
4.2. 选择要消除基本单元,并分析其特点
这个单元我选择的是偶数环及部分附属线,准确的来说是环内无点的偶数环,也就是说偶数环内部是可以有线的,我们来看看3-正则图内偶数环的特点。
如图9所示,偶数环必然是3色可染的,这些偶数环内部并无点,也无连接线。左图环线我们只用了A、B两色,偶数环外必然有偶数根线与偶数环相连接,且连接线全为第三色C色,也是偶数根线;中间图点1与点8连接我们用了第三色C色,而环外连线多了两根A色线,是偶数,环外总线数也是偶数;同理右图,我们用相对更复杂的3色染色,但环外与环上点相连的线都必然是偶数,且同一颜色的连接线也必然是偶数。我们再看看一些特殊的环内无点偶数环,我们让偶数环内有连接线,如下图10:

Figure 9. Even rings in 3-regular graphs
图9. 3-正则图内的偶数环
此图就是偶数环内有连接线,连接了点4和点8,那么依据3-正则图点、线连接方式,此时点4与点8将不可能再与外部其它点连接,又因为每一根连接线都连接两个点,所以偶数环内每多一个连接线,与环外点相连的连接线必然少两根,依然会保持偶数,同一色线也依然会保持偶数根;另外,上图10如果点1与点7连接,偶数环不与点9、15连接,那么这根连接线可以在环外部,但环上的点与环外的点之间的连接线还是会保有以上性质,就是线数是偶数,同一色线也是偶数。
值得一提的并不是所有3-正则图都存在环内无点且无线的偶数环,例如正12面体,每个面都是5条边,都是奇数环,但如果考虑环内无点且有线的情况,等同于我们把相邻的两个奇数环拼接成一个偶数环,这样在3-正则图里就必然可以找到偶数环了。
我们把3-正则图中环内无点的偶数环、偶数环上点之间的所有连接线,以及偶数环与外部点连接线数的一半(消除的点、线数量关系必须保证x = 2y/3)看做一个基本单元。
4.3. 说明偶数环消除法的染色步骤及注意事项
首先任何一个上文中选定的基本单元的线必然是3色可染的;在任意一个复杂的3-正则图里我们都可以一步一步消除这样的单元;那么剩下的线数,都必然是剩下的点所需要的,我们把剩下的点、线对应连接也必然还是一个3-正则图。按照这样一步一步消除的办法,我们最终会得到点数x = 4或者6的3-正则图,这些3-正则图都已经证明是3色可染的。最后我们原路返回,把每一步消除的单元加进来,并一步一染色,在这个过程中每一步只需要对新加入的单元的线3染色,而不会改变原有线的染色,至于点、线之间连接方式的改变我们可以原路复原,这样我们将可以得到任意无割边3-正则图线的3染色。
要注意的是一种特殊情况,我们消除的单元是3色可染的,因为在恢复过程中偶数环与外部点连接线的颜色的限定,偶数环并不全都是3色可染,但此时要形成新的3-正则平面图,会存在偶数环外部同一个点发出两条线与偶数环上两个不同的点连接,此时这两条线互换颜色将不影响上一个3-正则平面图染色,互换颜色后将可以对偶数环的线3染色;如果既不存在同一个点发出两条线也限定颜色造成偶数环线3色不可染,此时将无法形成下一个3-正则平面图,而我们每一个单元都是从3-正则平面图上消去的,所以恢复过程中不会出现此类状况。
4.4. 举例演示3-正则图染色步骤
下面我们以12面体所对应的3-正则图举例来说明我们的证明,我会选择一个一个的单元一步一步拆除,拆除过程中改变线的连接形成点数较少的3正则图,最后当x=4时我对这个3-正则图线染3色,并一步一步复原,在过程中一步一步染色,看我们是否能一次为正12面体的边线染色。如下图11就是正12面体对应的3-正则图:
第一步,加粗线部分是我选择的第一个偶数环及相关要拆除的线,拆除后及连接成新的3-正则图如下图12:
第二步,选择新的拆除单元,并拆除,如下图13:
第三步,连接成新的3-正则图,此时x = 4,对x = 4的3-正则图染色,如下图14:
第四步,开始还原一个单元,并染色,如下图15:
第五步,还原最后一个单元,并染色,如下图16:
如此,我们就给正12面体所对应的3-正则图的线3染色完毕。

Figure 11. 3-Regular graphs corresponding to a regular 12-face
图11. 正12面体对应的3-正则图
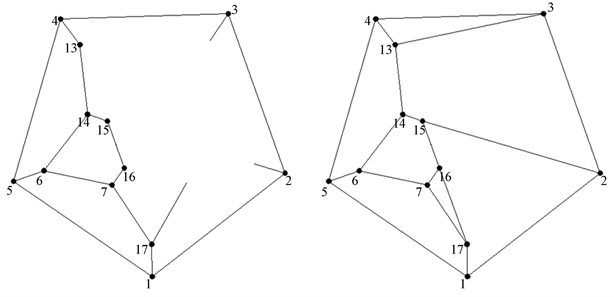
Figure 12. Remove the first unit and connect it to a new 3-regular graph
图12. 拆除第一个单元并连接成新的3-正则图

Figure 13. Select the second unit and remove it
图13. 选择第二个单元并拆除
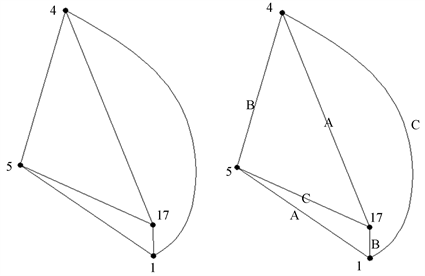
Figure 14. 3-Regular graphs with regression x = 4 and coloring
图14. 回归x = 4的3-正则图并染色
总结第二阶段的证明:如果给定一个3-正则图,我们总能在3-正则图内找到一个环内无点的偶数环,把这个环内无点的偶数环及其环上各点之间的连接线,以及环上各点与环外点之间连接线的一半数量的线看成一个单元,我们消除这个单元后一定还可以连接成一个顶点数变少的3-正则平面图;在我们不断消除此类单元的情况下,就一定可以得到顶点数x = 4、6等顶点数极少的3-正则图,然后我们可以给这个3-正则图的线3染色,并且可以把消除的单元一步一步恢复,恢复过程中即可完成原给定3-正则图线的3染色。
如果用一句话叙述,即如果一个3-正则图线3色可染,那么这个3正则图加入一个环内无点的偶数环及对应的若干连接线(点、线关系保持x = 2y/3),必然可以形成另一个线3色可染的3-正则平面图;又因为我们不限定环内无点偶数环的个数、顶点数及连接形式,且顶点数x = 4、6等顶点数极少的3-正则图3色可染,所以原则上我们可以做出任意的3-正则平面图,且所有3-正则图的线必然是3色可区分的。
5. 结论
至此,我们已经证明了开篇表明的两个观点,即第一证明3-正则平面图线的3着色与极大图点的4着色等价,第二证明3-正则平面图线的3着色是必然可以的。这也就等同书面证明了四色猜想是一个真命题。
现实中证明这个命题之所以困难,我分析原因主要是在极大图顶点数足够多,或者3-正则平面图线数比较多的情况下,正确解的数量会随之增加,过程中进入误区的概率也会更大。想要寻找一个固定解,那么因为解的不确定性,必然面临随机选择,如果这种随机选择不能保证是正确的方向,那下一步就是误区。而我们的方法,也存在随机性,但这种随机性只会在正确解的范围内波动,例如在3-正则平面图偶数环的消除过程中,不同的选择就可能会有不同的正确解。
以后的研究中,正解的数量与点、线数量的关系应该作为努力的方向。