自密实钢管混凝土合理膨胀剂参量研究

The Research of Reasonable Expansion Agent Dosage of Self-Compacting Concrete Filled Steel Tube

摘要: 本文分别进行了4根管径为219 mm和4根管径为273 mm、壁厚为8 mm的钢管混凝土轴心抗压试验，其核心混凝土膨胀剂参量分别为0%、5%、7%、9%。并通过有限元对核心混凝土膨胀剂参量分别为0%、5%、7%、9%，管径为219、273、350、400，壁厚为8的钢管混凝土进行分析。结果显示，膨胀剂参量为5%、7%时，钢管混凝土的承载力分别提高53.0%、44.5%；膨胀剂参量为9%时，钢管混凝土承载力反而有所降低。因此膨胀参量应控制在5%~7%较为合理。

Abstract: In this paper, the axial compression test of concrete filled steel tube with 4 pipe diameters of 219 mm and 4 pipe diameters of 273 mm and wall thickness of 8 mm was conducted respectively, which the core concrete expansion agent parameters are 0%, 5%, 7% and 9% respectively. And the finite element model was used to analyze the core concrete expansion agent parameters of 0%, 5%, 7%, 9%, and pipe diameters of 219, 273, 350, 400 and wall thickness of 8. The results show that when the expansion agent parameters are 5% and 7%, the bearing capacity of the concrete-filled steel tube is increased by 53.0% and 44.5%, respectively. When the expansion agent parameter is 9%, the bearing capacity of the concrete-filled steel tube is reduced. Therefore, the reasonable expansion parameters should be controlled at 5% to 7%.

1. 引言

钢管混凝土利用套箍作用，充分的发挥钢材的抗拉性能和混凝土的抗压性能，使得钢管混凝土承载力高、延性好、节约建筑材料，减小占地空间，且钢管混凝土浇筑不需要搭模板，施工方便快捷，不受季节影响，能有效降低结构成本；因此钢管混凝土的应用也越来越广泛。大量研究发现混凝土凝固会产生收缩变形，使得钢管与核心混凝土接触不充分，在钢管混凝土受压屈服前，钢管混凝土环向受拉性能没有完全发挥。为了使核心混凝土与钢管接触更加充分以及钢管环向受拉性能能够充分发挥，在核心混凝土中参入膨胀剂，使核心混凝土在凝结硬化过程中体积增大，混凝土凝结硬化产生的收缩变形得到补偿，当膨胀剂参量达到一定值时，钢管环向抗拉和混凝土抗压的性能能得到充分的发挥，提高钢管与混凝土之间的协同工作性能，使钢管混凝土承载力达到最大。因此合理膨胀剂的参入可以使得选用较小截面尺寸的钢管混凝土而得到相同的承载力，同时降低自重和节约建筑材料。

李乃珍，谢敬坦等人 [1] 对全补偿型混凝土膨胀剂及其对高强混凝土干缩的补偿进行了研究，认为FEA100用于C50~C90高强混凝土时，可使其干缩得到80%~100%的补偿；随着膨胀剂参量增加，自密实混凝土立方体抗压强度、劈裂抗拉强度和轴心抗压强度先增加后降低，存在峰值，膨胀剂参量对自密实混凝土弹性模量的影响不明显；膨胀剂的参入提高了自密实混凝土的抗压强度、劈裂抗拉强度和轴心抗压强度 [2] [3] [4] [5] [6]。祁璐帆 [7] 进行了膨胀剂对钢管混凝土瞬时变形和徐变的影响研究，膨胀剂会改善钢管混凝土的力学性能，随着膨胀剂参量的提高，钢管混凝土在轴压下的瞬时变形和徐变相应减小。基于ABAQUS有限元模拟的钢管失效研究解析方法计算结果与有限元模拟结果符合，因此，轴向偏心载荷模型可为钢管混凝土结构的设计及校核提供参考 [8]。

2. 理论分析

钢管混凝土构件未受荷载前，钢管与混凝土之间存在三种关系如图1：未加膨胀剂或膨胀剂参量较小时，钢管与混凝土之间存在间隙；钢管与混凝土刚好紧密接触；钢管与混凝土之间存在一定的初始挤压应力。当钢管与混凝土之间存在间隙时，在荷载施加初始阶段，钢管与混凝土的应力都比较小，横向变形也十分微小，钢管与混凝土之间各自独自受力，随着荷载的增大，钢管与混凝土的泊松比增加，钢管与混凝土横向变形增加，使钢管与混凝土接触并产生挤压，钢管的应力状态为纵向压缩和环向的拉伸如图2；核心混凝土受钢管的约束处于三向受压状态，其抗压强度增大。当核心混凝土达到三轴抗压强度时，钢管环向应力并未达到最大，其抗拉性能没有得到充分的利用。对于后面两种情况，钢管与核心混凝土从开始加载就协同受力，但是膨胀剂参量过大时，当核心混凝土达到三轴抗压强度时，钢管的环向拉应力已经处于下降段，使钢管混凝土承载力降低。在合理膨胀剂参量下，核心混凝土在达到三轴抗压强度时，钢管的环向拉应力刚好达到最大，钢管对核心混凝土约束效果达到最佳。

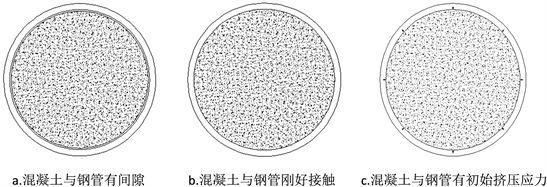
Figure 1. Schematic diagram of three initial states of concrete filled steel tube

图1. 钢管混凝土三种初始状态示意图

钢管混凝土横向受力分布如图2，在钢管的约束下，其核心混凝土强度有以下几个计算公式 [9] ：

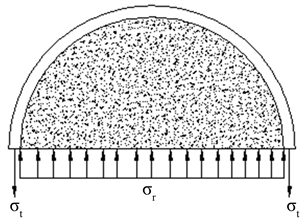
Figure 2. The transverse stress state of concrete filled steel tube

图2. 钢管混凝土横向应力状态

1) 三向受压混凝土强度计算式：

${\sigma }_r=\frac{{\sigma }_t\times 2t}{d}$ (1)

$f_{cc}=f_c+k{\sigma }_t$ (2)

式中 $f_{cc}$ -核心混凝土的极限强度， $$ -混凝土立方体抗压强度， ${\sigma }_{\text{t}}$ -钢管对核心混凝土的侧压力，k-套箍系数，d为核心混凝土直径，t为钢管壁厚。

2) 钢管混凝土统一理论承载力计算简化公式为 [10] ：

$f_{sc}=\frac{1+1.5\xi }{1+a}{f}_{ck}$ (3)

式中： $f_{\text{s}c}$ 为组合体抗压强度， $\zeta$ 为套箍系数， $\zeta \text{=}\frac{A_s{f}_y}{A_c{f}_{ck}}$ ，a为含钢率， $a=\frac{A_s}{A_c}$ 。

3) 约束混凝土理论核心混凝土强度计算式：

$f_{cc}=\left(1+k\right)f_c$ (4)

式中k为套箍系数，因此钢管混凝土承载力为：

$N_u=A_s{f}_s+f_{cc}{A}_c$ (5)

为了确定在膨胀剂作用机制下钢管混凝土极限承载力计算式，本文设计了两组钢管混凝土试件：钢管直径为219 mm，壁厚为8 mm，核心混凝土膨胀剂参量分别为0、5%、7%、9%；钢管直径为273 mm，壁厚为8 mm，核心混凝土膨胀剂参量分别为0、5%、7%、9%。并进行了钢管混凝土短柱轴心受压试验。

3. 试验内容

3.1. 试件制作

试件分两组，分别为直径219 mm及273 mm，材料为Q345钢管，壁厚均为8mm，核心混凝土强度等级为C50，膨胀剂掺量分别为0、5%、7%、9%，作为对比，每组中一个试件不填充混凝土(空钢管)，试件高度均为750 mm。试件一端先焊接一块400 mm × 400 mm × 25 mm钢板，然后浇筑混凝土(自密实)并做留样处理，待混凝土凝结硬化后，用砂浆抹平顶面，用同样尺寸钢板焊接，试件规格及材料基本性能见表1~4。

Table 1. Test piece specifications

表1. 试件规格

Table 2. Mechanical parameters of steel pipe

表2. 钢管实测力学参数

注：数据来源主要是将空钢管进行轴心抗压试验测试所得。

Table 3. Mechanical parameters of concrete sample block for 28 days of curing

表3. 混凝土留样试块养护28天的力学参数

说明：体积改变量=实测体积-标准立方体体积。

Table 4. Test piece column

表4. 试件一栏表

注：其中约束效应系数 $\theta =\frac{A_S{f}_y}{A_c{f}_{ck}}$ ，A_s为钢管横截面面积，A_c为钢管混凝土中混凝土截面面积，f_y为钢管屈服强度，f_ck为混凝土轴心抗压强度标准值，取值为f_ck = 0.67f_cu，f_cu为立方体抗压强度标准值。

3.2. 试验装置

该试验在贵州大学土建实验室进行，自密实钢管混凝土试验装置如图3所示，采用YAJ-10000微机控制电液伺服压力试验机进行加载，在钢管外侧中部对称四个位置贴大小为3 cm长度的应变片，每个位置的2个应变片相互垂直，应变片位置示意图如图4所示，然后采用静态应变测试仪(DH3818-2)进行应变数据的采集与记录；采用RLX50A-1000拉线式位移传感器测构件纵向变形。

Figure 3. Test device diagram of the strain gauge

图3. 试验装置图

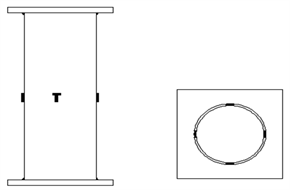
Figure 4. Schematic diagram of the position

图4. 应变片位置示意图

3.3. 加载过程及试验现象

将安装好所有装置的钢管柱推到压力机上，加载速率为30 KN/s进行快速加载，在荷载达到屈服前，构件无明显变形。当荷载持续加载至屈服荷载时，钢管两端与垫焊接位置及中部出现鼓曲，且随着荷载持续增加，鼓曲的幅度增大，但钢管中部变化比端部略小；当荷载接近极限荷载时，钢管中间沿45˚局部鼓曲；当荷载达到最大后，承载力开始下降，最后在钢管中部出现一条与轴线大约呈45˚的斜裂缝。

3.4. 试验结果如表5所示

Table 5. Results of axial compression test

表5. 轴心受压试验结果

注：由于压力机的限制，部分构件未压坏或未做。Nu1：按钢管混凝土统一理论计算极限承载力；Nu2：按式(5)计算极限承载力。

4. 试验结果与分析

根据表5统计结果，没有参膨胀剂的钢管混凝土极限承载力与统一理论计算的结果相差2.1%，与统一理论计算结果接近，说明钢管混凝土统一理论对未参膨胀剂钢管混凝土承载力的计算吻合度好；而对于膨胀剂参量为5%、7%的钢管混凝土，其极限承载力比统一理论计算的结果分别提高了53%、44.5%，承载力提高效果相当明显，钢管混凝土统一理论对参人膨胀剂的钢管混凝土极限承载力计算吻合度较差；膨胀剂参量为9%的钢管混凝土极限承载力比钢管混凝土统一理论计算结果提高16.5%，承载力提高效果不是很明显。通过绘制屈服承载力和极限承载力与膨胀剂参量的关系见图5，可以看出随着膨胀剂掺量的增加，自密实钢管混凝土的极限承载力呈现先增加后降低，膨胀剂参量在5%~7%之间时钢管混凝土承载力提高幅度较大，因此膨胀剂参量应控制5%~7%之间较为合理，同时通过表5可以看到当钢管混凝土参入合理膨胀剂后，极限承载力宜使用式(5)计算。

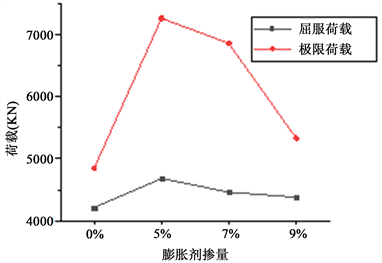
Figure 5. The relationship between the yield load and the ultimate load of the first set of specimens and the amount of expansion agent

图5. 第一组试件屈服荷载和极限荷载与膨胀剂掺量的变化关系

试验的记录和数据处理，得到了如图6所示的不同膨胀剂掺量钢管混凝土短柱轴心受压应力应变曲线和荷载位移曲线变化关系。

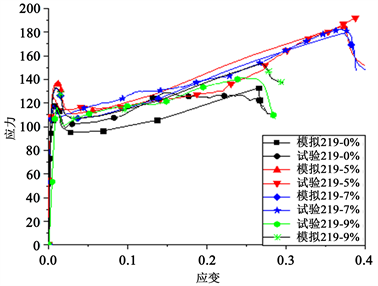
Figure 6. Comparison of experimental values and numerical simulations of concrete with diameter 219 and different expansion agent parameters

图6. 直径219、不同膨胀剂参量钢管混凝土试验值与数值模拟对比

1) 从应力–应变曲线来看，从刚开始加载到接近屈服点时，它们近似重合，所以弹性阶段的弹性模量并无太大差别，单一曲线整体变化趋势(指曲线的走势)相似，从四组曲线总体可以看出，随着膨胀剂掺量的增加，自密实钢管混凝土的屈服应力和极限应力先增加后降低。

2) 由直径为219 mm的不同膨胀剂掺量钢管混凝土应力–应变曲线可知，膨胀剂掺量为5%、7%时，极限应变与极限承载力均明显提高。由于直径为273 mm钢管混凝土试验曲线无下降段，由于机械条件限制，导致数据不足，得不到更准确的结论。

同时通过在钢管混凝土环向和纵向的应变片采集了随着荷载的增加，环向及纵向的应变与荷载的关系如图7所示，其中纵向应变为负，环向拉伸应变为正。

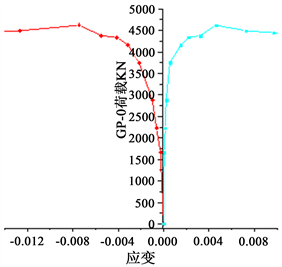(a) 膨胀剂掺量0% 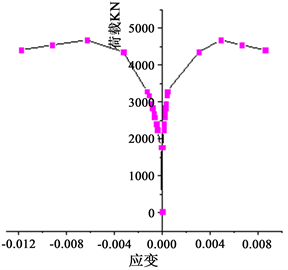(b) 膨胀剂掺量5% (c) 膨胀剂掺量7% 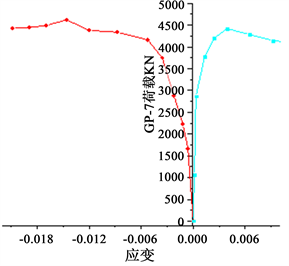(d) 膨胀剂掺量9%

Figure 7. The relationship between the load of different expansion agents and the longitudinal strain and the circumferential direction

图7. 不同膨胀剂掺量荷载随纵向应变和环向变化关系

由图7可以明显看出膨胀剂掺量为0%、5%、的钢管混凝土构件在屈服时，其环向拉伸应变均在0.004左右，纵向应变均在−0.006左右，而膨胀剂掺量为7%的钢管混凝土构件在屈服时，其纵向应变和环向应变分别为−0.008和0.005，其抗压刚度相比前两种钢管混凝土构件的抗压刚度要小，膨胀剂掺量为9%的钢管混凝土构件，在荷载达到屈服时，纵向和环向应变分别为−0.1和0.008，纵向抗压刚度减小的十分明显；且图7可以看到膨胀剂掺量为5%时，其纵向抗压刚度最大，产生以上现象的主要原因是：对于膨胀剂掺量为0%的钢管混凝土构件，由于混凝土收缩变形，导致混凝土与钢管之间没有完全的接触，不能充分发挥协调受力，而膨胀剂掺量为5%和7%的钢管混凝土构件在混凝土凝结硬化过程中会产生体积膨胀，消除了混凝土收缩变形引起的脱空现象，钢管与混凝土能很好的协同受力；当膨胀剂掺量为9%时，混凝土的体积膨胀大于混凝土的收缩变形，且钢管两端用钢板焊封，导致钢管的环向产生较大压力，在外荷载作用下，钢管环向较早的进入屈服，其环向应变迅速增大，对混凝土约束效果减弱。降低了钢管混凝土的承载力。

5. 模拟试验及分析

为了验证膨胀剂对钢管混凝土的力学性能的影响，本文利用有限元软件ABAQUS进行建模分析，为了探究套箍系数与膨胀剂对构件承载力的影响，在直径为273和219的基础上，新增了直径为350和400两种管径，其他条件保持不变；针对不同膨胀剂参量的钢管混凝土，其中钢管设置为壳单元，混凝土为实体单元；并将分析结果与试验进行对比分析见图8。

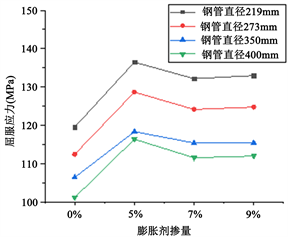
Figure 8. Relationship between different expansion agent dosages and different diameters and yield stress of concrete filled steel tubes

图8. 不同膨胀剂掺量和不同直径与钢管混凝土屈服应力的关系

从图8可以看到，随着套箍系数的降低，屈服应力逐渐下降，说明钢管对混凝土的约束效应逐渐削弱；随着膨胀剂的增加，钢管混凝土的屈服应力逐渐增加，当膨胀剂掺量为5%、7%时，屈服应力及极限强度提高明显，当膨胀剂掺量为9%时，屈服应力及极限强度提高幅度降低，说明钢管混凝土在膨胀剂参入量在5%~7%之间较合理高。因此建议钢管混凝土膨胀剂参入量应控制在5%~7%，通过曲线拟合，得到了钢管混凝土承载力放大系数与膨胀剂变化关系如图9所示。

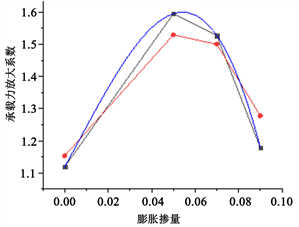μ=1.12+12.26X+37.33X²−1847.23X³ (X取值0~0.09)，黑色线为试验极限承载力值与理论极限承载力比值，红色线为数值模拟极限承载力值与理论极限承载力比值，蓝色曲线为拟合曲线。

Figure 9. Fitting curve

图9. 拟合曲线

6. 结论

1) 适量膨胀剂的掺入，不仅能提高钢管混凝土屈服荷载和极限荷载，且能改善钢管混凝土变形能力。

2) 试验研究所针对的几组膨胀剂掺量结果显示，膨胀剂参量为5%、7%时，屈服承载力与极限承载力明显提高，能充分发挥钢管与核心区混凝土承压协同作用，膨胀剂参量宜取5%~7%之间。

3) 本课题通过钢管混凝土短柱轴心受压试验，研究膨胀剂掺量对构件承载力及延性的影响，得到试验条件下的膨胀剂合理掺量，为江凯河特大桥工程施工提供了理论支持。

NOTES

^*通讯作者。