1. 引言
微分几何的历史源远流长,尤其在近现代它得到了蓬勃发展,微分几何跟其他学科的联系也更为紧密,现在已成为数学领域的一个主流方向。随着这门学科在内容和方法上的不断更新,迫切需要本科生除了掌握古典微分几何的知识外,尽可能地熟悉一些现代微分几何的理论方法。本文我们从几年的课程教学中提出一些看法,再探索下微分几何教学的一些方法。
2. 存在的问题
近几年我们先后使用了两个教材,一个是梅向明和黄敬之编著的《微分几何》 [1],另一个是彭家贵和陈卿编著的《微分几何》 [2]。在这两本教材的教学中,我们发现学生在学习微分几何时碰到不少困难。下面是学生在课程学习中普遍遇到的几个问题:
1) 缺乏微分几何与其他课程的联系
微分几何的很多理论建立在其他学科的基础上,但很多学生在学习时,知识是断裂的,不能灵活运用其他理论到微分几何中去,比如证明曲面第一基本形式正定性时想不到解析几何中的Lagrange恒等式。在展开曲面论时,不能熟练运用二元微积分中的求导、极值原理等。讨论曲线论基本定理时不能利用常微分方程组解的存在唯一性,证明曲面论基本定理时理解不了偏微分方程组解存在的可积性条件,恰好是曲面的Gauss方程和Codazzi方程。
2) 缺乏抽象理论与具体实践的结合
随着课程的深入,一些数学概念变得越来越抽象,以致学生们经常会遇到这样的问题:学了一大堆抽象的理论,但遇到具体的曲线和曲面时不会计算。比如计算双曲抛物面的主曲率、平均曲率、高斯曲率,并计算这个曲面沿一条曲线的法曲率、测地曲率时,学生对这么多概念非常迷惑,分不清它们之间的关系。一方面是学生对概念的理解不够深入,还有就是对具体的曲线曲面缺少计算,遇到具体问题就无从下手。
3) 计算能力和几何直观能力不足
古典微分几何的主要工具是向量运算与微积分,向量运算中的一个主要问题是不能利用Frenet标架的正交性,在多次求导后公式变得很复杂,从而不能简化公式得出结论。微分几何学习时要不断的求导,要出来好结果必须熟练计算高阶导数。又由于曲面有两个参数,就要用到多元微积分,学生在多元函数的高阶导数计算上,能力明显不足。微分几何处理的是曲线与曲面,其图形各有特点,曲线与曲面上的几何量也需要根据图形来理解。学生没有养成作图的好习惯,也不善于作合适的图,只有死记硬背公式,缺少通过图形来分析的能力。
4) 几何课程与课时显少
微分几何教学只有每周4个课时,一方面要包括古典微分几何的重要内容,又要较快引入了“活动标架”、“外微分”、“协变微分”等现代内容,以致部分内容不能更详细的展开,正如彭家贵和陈卿在 [2] 中提到“一些局部理论的内容放在习题中,是作为正文内容的一个补充”。数学系本科生的几何课程也很少,只有解析几何与微分几何。因此学生的几何意识不浓,认为几何只是数学的一个小方向,不用重视。学生学了解析几何后,以为用代数方法处理简单的曲线曲面就够了,等碰到微分几何用微积分来研究复杂的曲线曲面时感到很不适应。
3. 一些教学探索
微分几何具有它自身的特点,一方面它跟微积分、代数、方程、拓扑等课程发生紧密联系 [3] [4]。因此需要学生有扎实的数学基础,尤其是深厚的分析功底。另一方面它提出许多新的思想及方法,这对学生的知识消化提出新的挑战。下面浅谈下本科微分几何的教学体会。
3.1. 加强知识交叉及新理论运用
曲面论涉及到二元函数的求导,单纯计算不仅复杂而且很难提取出关键的信息。因此一个方法是引入线性代数的矩阵理论来处理微分几何的内容。比如把曲面的第二基本形式写成矩阵形式
来推导就非常方便。让学生学会通过Jacobi矩阵来验证一些几何量不依赖于参数的选择,通过矩阵描述它们在不同标架下的形式及其相互关系。
研究曲面几何时,要让学生学会利用张量分析、活动标架、外微分这些新的方法。在讨论曲面基本论定理时,让学生熟练运用张量符号的运用与推导。通过张量形式的计算呈现出Gauss绝妙定理,自然而然地让学生体会到新方法的威力。在讨论曲面的运动方程和结构方程时,用自然标架和正交标架这两种手段,让学生能感受到它们各自的特点,及用外微分工具来描述所带来的简洁性与灵活性。讨论主曲率为常数的曲面分类中,采用活动标架法,让学生学会怎样利用现代的工具来解决问题。引进外微分形式时可以引入数学分析中的二重积分的参数变换。当二重积分换元时多出个Jacobi行列式:
其实积分积的不只是被积函数,而是这个对象
,上式的积分符号后面就是这个对象在不同参数下的形式。考虑到行列式符号的变化性质,把它写成
更合适,这就是二阶外微分形式。
3.2. 加强实践及计算能力
课堂教学中,不宜侧重于抽象的理论,要更关注于具体的几何对象。微分几何内容的一个特点是复杂的导数计算,课堂时间训练不够,布置课后练习让学生培养出对待复杂公式的计算能力。
介绍曲线局部理论时,让学生利用圆柱螺线这个典型例子来计算它的弧长参数、Frenet标架与Frenet公式、曲率与挠率。这相当于通过这个例子把曲线论中的所有几何量及公式都复习一遍,以让学生理解其中的公式及其相互关系。在曲面论中让学生会计算常见曲面的两个基本形式、法曲率、主曲率、Gauss曲率、运动方程和结构方程等,这相当于又把曲面论中的理论验算了一遍。引导学生通过具体的计算来理解曲面的特点,比如通过计算球面的两个基本形式,发现它们成比例,马上想到球面沿任意方向的法曲率相等都为常数,因此球面的主曲率相等,是全脐点曲面。柱面、旋转曲面等其他曲面也要逐个计算。
3.3. 加强几何直观
学生做题时,经常感到学了不少公式却无从下手。一方面原因是对几何对象的空间感不够,因此一定要让学生在旁边先画图,根据图形来思考。比如在讲解曲面沿其上一条曲线的测地曲率和法曲率时,很多学生就弄不清它们之间的各种关系。这个问题的关键的是画好图1。取一个正交标架(曲线切向量t,曲面法向量n,及跟它们垂直的向量e),再画上曲率向量及它在这个正交标架上的投影,这样所有的信息都可由这张图得到。

Figure 1. The orthogonal frame of surface
图1. 曲面上的正交标架
在计算及证明中,选取好的坐标及参数可以简便不少。微分几何中的很多情形是第一步走好了,就迎刃而解,下面我们举一个例子来说明。
例:若曲面S与平面X相交于o点,且S位于X的同一侧,证明X是曲面S在o点的切平面。
分析:学生碰到这样没图形且没公式的题目,感觉无从下手。那首先画一个曲面S和一个平面X。为了容易计算,想到选取一个直角坐标系:使S与X的交点o为原点,平面X作为坐标系的xoy平面,且由题设不妨设S位于xoy平面的上面,参看图2。这样曲面在o点附近可以由某个函数f(x,y)给出,题目的假设就蕴含函数f(x,y)在o点达到了极小值,因此由二元函数的极值原理得出曲面在o点的切向量落在了xoy平面上,因此X就是S在o点的切平面。
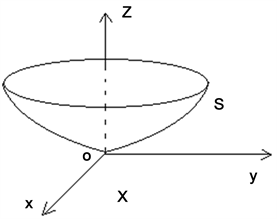
Figure 2. The surface S and its tangent plane X
图2. 曲面S与它的切平面X
3.4. 增加课时与课程内容
对待学生如何学好微分几何的一个措施是增加课时与教学内容,这能提高这门学科在学生心中的重要性,也能让学生更系统更扎实的学习。一学期课程建议每周5个课时,教学首先要包括曲线及曲面论中的大部分内容,同时为了适应微分几何发展的需要,要求尽量介绍现代微分几何的新理论。以彭家贵和陈卿编著的《微分几何》 [2] 为例,教学内容包括前五章。在曲线论的正文中,可增加空间曲线在普通参数下的曲率与挠率公式。教师也可介绍下一般的Stokes公式及它与数学分析中相关公式的联系,由此可培养出学生的几何兴趣。
致谢
非常感谢审稿专家和编辑对本文提出的宝贵意见。