1. 连接整体说明
接口的连接就如同积木凹凸槽相互连接,通过连接形成形态各异的整体。当然接口也是多种多样,可以像钉子固定两块物体,胶水粘贴物体等,甚至输入和输出也可以看成是一种连接。而拥有输入和输出的连接个体,可以形成输入和输出连通的整体。通过判断输入和输出的值是否都流经这些个体,来选择最短的连接整体。之后再加入接口状态值,可以用0,1,−1分别表示接口状态的正确,错误和未执行,将这些接口状态值理解为调整层。调整层调整选择出来的连接整体,让它适应多种输入和输出,优化连接个体的形成过程。
通过输入和输出方式进行连接,最容易想到的是编程里面的各种方法函数。把一个函数看成是连接的单体,把输入方法的参数作为输入的值,方法的返回值作为输出的值 [1]。那么不同方法之间可以通过值连通,间接地实现方法之间的连接。多个方法函数的相互连接形成整体,这个整体就是我们要完成某一项任务的整体。形成整体的过程就像蚂蚁寻找食物一样,一开始先随机不重复路径地寻找,蚂蚁找到食物后,就用信息素加强食物和巢穴之间的路径。对应着方法连接里面的,如果方法少的话就遍历一遍方法的不同连接组合,如果方法多的话就提取一定量的随机不重复的组合 [2]。之后保留输入和输出值流经的方法,去掉其它没有都值流经的方法,就是想要的连接输入和输出的方法整体。
随着输入和输出的增多,到达这些输入和输出的链路就会形成一个网络,类似于黏菌形成的食物网络,或者城市里面的道路网络 [3]。虽然这些网络可以到达每个点,但它并不具备单条链路那么明确的起始和结果对应关系。比如你想要从一个起始点到达一个结果点,那么通过这个网络它可能会给出很多条到达的方式。它并没有很明确地告诉你哪条是最优的。想要得到最优的路线,如果你单纯地用距离最短的条件来判断,随着其它条件的加入这个判断也会失效,比如是否堵车,是否车辆通行等。因此每一种连接个体形成的整体就需要加上很多各自的判断条件。
要是把上面的判断条件看成是由很多基础判断条件形成的整体,那么通过这些基础判断条件形成的判断整体,就可以拼接形成适应多个输入和输出的模式。也就是把判断条件的形成,也当成一个整体来形成。按照这种思路,任意选择其中的一个输入点和输出点,在训练接口连接的同时也训练判断条件的整体连接就可以实现最短链路的选择。但会出现问题,因为判断条件并不拥有类似于接口一样的可以相互连接,因此需要把判断条件转换为公共的连接单元—数值的连接。用数字1,−1,0来表示判断条件的正确,错误和未执行状态。然后定义1,−1,0组合或者相消的连接规则。这样就相当于所有的判断条件都变成了1,−1,0状态链。而连接整体则以这个状态链为值,状态链的运行方法为基本连接单元。同理可以把判断方法也用接口连接的方式来表示,并且参与到接口构建中。为了方便,把判断条件及1,−1,0的状态值共同组成的层称为调整层。
接下来就通过一个例子来说明调整层和形成层的相互作用。为了更加明确地表达,并且利于计算和推导,把接口的连接转换为数字的运算。连接的方法就变成数字运算的方法,比如加,减,乘,除,求平均等。值的连接就变成了数字的传递,起始的输入就是起始的数字,结果的输出就是运算的结果。
2. 自动调用公式
2.1. 例子
我们用excel表格统计各种数据时,经常会用到公式来计算结果。但并不是每个人都能很好地使用公式,选择什么区域,选择哪些方法等都会困扰初学的使用。如果用接口模型的话,就可以实现只要选择起始区域的数据和结果区域的数据。它就可以直接调用库内的函数,通过连接形成公式整体来完成计算。先来做个excel简单的例子:比如需要统计某个班级学生各门成绩的总和和平均值。现在拥有的数据是前面几次已经统计完成的表格作为训练值。训练只提供学生各门的成绩,根据训练的结果自动求出结果。如下图1所示:
2.2. 形成层
分析上面的例子,它存在着加法和求平均值两个运算方法。输入的数值为math,Chinese,history,extra,pass这5种数据,并且存在extra,pass这2种干扰数据。输出的数值为求和的值。因此模型的接口包含两个输入接口和一个输出接口的加法,两个输入接口和一个输出接口的求平均值。求平均值的输入是两个数据,并且记录它的个数长度,然后根据长度和值计算平均值。如果数据不多,就直接遍历运行。第一次运算,5种数据两两组合再和加法组合,有25种组合。第二次运算,有30 * 30种组合。第二次运算完成的时候,已经可以匹配到求和的结果了。之后通过选择起始的值和结果的值都流入的方法,去掉其它的方法,得到到达这个结果的方法组合。求和运算完成后,求平均值的方法也作类似的运算。把上面的运行模式成为形成层,可以简单概括为:拥有输入值并且调用方法库来形成结果值,通过接口值筛选形成的方法整体 [4]。如下图2:
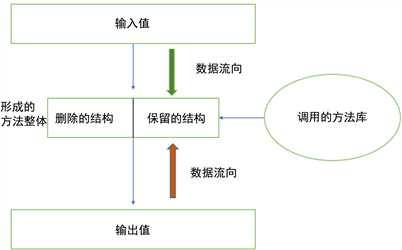
Figure 2. Formation of a layer structure
图2. 形成层结构图
再运行一次获得它的形成整体,接下来几次运行优先调用方向对的整体。如果能够到达求和的结果,就不作改变,如果没有到达求和的结果,就再次进行组合,并且把新的组合也进行记录。这样处理后就可以得到这个输入和输出的运算方法组合。但组合的结果可能会比较混乱,求和与求平均值的结果混在一起,甚至包括很多的分支,因此需要进一步优化。
2.3. 调整层
为了处理混乱的结果,先把每组数据的运算状态记录下来。用1,−1,0来表示每个公式数值的状态,1表示正确,−1表示错误,0表示没有运行。运行求和的时候争取使用了求和公式则记录值为1。运行求和的时候却运行了求平均的公式,则记录值为−1,0表示没有被运行。为了获得更多可以相互区分的值,这里也一同把数值的附带信息,如math,Chinese等的信息一同用1,−1,0来表示。这样每个同学的成绩都运算一遍之后,方法组合里面的每个值就会形成各自的一长串的1,−1,0的状态链。
查看这些状态链,从单个方法分析,如果把方法的输出状态链−1变成0,就是我们想要的正确的输出结果。把这个修改后的状态链作为结果值,同时把方法输入值的状态链和它附带信息的状态链作为输入的值,加上对这个状态链进行处理的规则,就可以构成一个连接模式。方法处理包括对状态链进行叠加(1与−1为1,1与1为1,0与−1为−1,0与1为1),相消(1与−1为−1,1与1为1,0与−1为−1,0与1为0)等方法来连接状态链。通过输入值的状态链和连接方法,形成与结果最匹配的值作为调整值,就是一个完整的接口连接模型。结果匹配原则一般是可多不能少,需要包含结果状态链里面的每一个1。这样提取出最接近的值就是这个模型的调整方法。把上面这种状态链插入的运行模式称为调整层,概括他的运行过程为:把判断信息转换为状态链,然后做跟形成层类似的方法构建和结果选择模式。如下图3:
宏观分析,状态链的作用就是信息的拼凑。比如对拥有math的信息、拥有Chinese和拥有history的信息进行拼凑,可以得出求和的状态链路。而平时运行的时候,只有同时出现求和的状态信息为1和分项状态信息为1的时候才会运行。如果出现的是求平均值,那么就不会运行这个组合,而只会运行求平均值相应的组合。其它的优化还包括先形成整体的分支,通过状态链的匹配程度来避免多余的分支。根据最佳匹配,一些完全被包含的分支则会因为没有被运行过而被删除。根据上述的方法就可以把上面混乱的方法整体,调整为根据起始输入和输出选择最佳模式。
根据随机组合的方式可以说很糟糕。一个最简单的加法以及很少的几个输入数字就会产生30 * 30种组合。因此需要对其进行优化,优化的方法就是在它上面加上一个调整层,通过调整层的参数选择来减少这种组合数量。比如调整层可以添加“结果相减是否大于0”,“结果值是否包含求和的值”的判断条件。并且把30 * 30个组合都做一次调用,调整层根据判断条件的状态拼接出最匹配的判断对应关系。这样处理后,相当于使用是否出现求和的输入值和是否大于0来组合判断。符合这个判断后,再运行相应的方法,从而减少很多的多余运算。
这里加入调整层看起来有些唐突。但是因为形成接口的基本连接单元是不同的,每个连接单元可能都有自己的判断条件。因此没有办法用一个统一的判断模式来管理这些不同连接单元的整体。比如“是否等于运行的值”可以认为是比较统一的判断条件,但还是会包含很多各异的判断条件,比如“基于向量的方法”,判断条件也可能是“方向是否正确”,仅仅用值判断准确性也会降低很多。因此这里把判断条件,也形成相同的构建模式,通过基础的判断条件,来形成适应个体的判断条件整体。
2.4. 形成整体的调用和嵌套
上来例子连接形成的“加法运算”或“平均运算”,也可以嵌入调整层。相当于加法或平均值运算与它的调整层一起构成了一个简单的接口模型。而这个“加法的接口模型”又被整个模型调用。也就是他们之间也可以相互调用,通过形成层和调整层形成接口模型。这个方法的输入和输出就是起始值和结束值。通过值的连接可以跟别的接口模型一起调用形成更大的接口模型。同时小的方法也可也嵌入调整层来形成小的接口模型。
通过接口模型构建形成的方法相对于普通函数方法的优点有以下几点:1) 构建形成的方法可以在使用的过程中让自己更加适应当前模式的运算。比如上面的构建后的加法运算,一直在运算求和环境下使用,就不会运算超过结果和的组合。而如果在其它环境,也可以再次根据新环境来形成新的接口模式。2) 他们可以根据初始数据和结果数据直接构建函数方法,不用人为地去掌握这些方法并且人为去调用。
接口模型对数字的运算,并不是因为它本身拥有简化运算过程,或者是模拟各种函数的效果。它优化的方法是使用各种现成的函数,组合连接形成实现运算结果的整体方法,并且通过调整层来进行优化过程。可以说它是通过使用现有函数和相应配套规则,来达到对数字进行运算的目的。这种通过输入和输出组合的接口连接模式,可以运用在未知函数的构建,甚至可以用在物质合成等领域 [5]。
3. 总结
从个体形成到整体的优化算法,通过以接口单元为基础,构建形成整体。并且流经这些接口单元的值作为选择的值,保留正确的值的接口连接。之后根据接口值运行的判断状态,并且把这些判断状态也作为基础的连接单元,来形成判断整体。形成的判断整体可以对多个目标和多个分支的运行,进行最优化的处理。通过以函数为单元,根据训练数据形成相应的函数功能整体,来说明它的运行模式。这样处理后就形成了以基础连接单元,形成适应结果条件的连接整体,说明了个体形成整体采用的方法和过程。