一类三阶半线性时滞微分方程振动准则

Oscillatory Criteria for a Class of Third Order Semi-Linear Delay Differential Equations

摘要: 研究一类三阶中立型半线性时滞微分方程，在最近参考文献结果的启发下，探讨不同条件采用了Riccati变换函数以及经典不等式等方法技巧，确立了方程的若干个新振动结果。文献中的一些结果得到了较好推广和改进，并给出了定理的应用。

Abstract: The class of third order neutral semi-linear delay differential equations is studied. Inspired by the recent reference results, some new vibration results of the equations are established by using Riccati transformation functions and classical inequalities under different conditions. Some results in the literature have been well extended and improved, and the application of the theorem is given.

1. 引言

考虑一类三阶中立型半线性时滞微分方程

${\left[r\left(t\right){\left|u^{″}\left(t\right)\right|}^{\theta -1}{u}^{″}\left(t\right)\right]}^{\prime }+q\left(t\right){\left|x\left(\tau \left(t\right)\right)\right|}^{\theta -1}x\left(\tau \left(t\right)\right)=0$ , $t\ge t_0$ (E)

假设以下条件都成立

(H₁)： $u\left(t\right)=x\left(t\right)+p\left(t\right)x\left(\sigma \left(t\right)\right)$；

(H₂)： $r\left(t\right),\sigma \left(t\right)\in C^{rd}\left(\left[t_0,\infty \right),\left(0,\infty \right)\right),p,q,\tau \in \left(\left[t_0,\infty \right),R\right)$；

(H₃)： $\tau \left(t\right)\le t,\tau \left(t\right)\le t,{\tau }^{\prime }\left(t\right)>0,\underset{t\to \infty }{\lim }\sigma \left(t\right)=\underset{t\to \infty }{\lim }\tau \left(t\right)=+\infty$；

(H₄)： $0\le p\left(t\right)\le p_0<1,q\left(t\right)>0,r\left(t\right)>0,r^{\prime }\left(t\right)\ge 0$。

若连续可微的函数 $x\left(t\right)$ 在定义域上是满足方程(E)的非平凡解，即方程(E)是拥有无数多个零解，我们就说它是振动的；不然，就称它为非振动的，也就是说，方程最终是一个正解或是一个负解。若

$\Omega \left(t\right)={\displaystyle {\int }_t^{+\infty }\frac{1}{r^{\frac{1}{\theta }}\left(s\right)}\text{d}s}=\infty$，则称 $\Omega \left(t\right)$ 是正则的，否则称 $\Omega \left(t\right)$ 是收敛的。

近年来，许多数学学者对二阶、三阶半线性中立型阻尼泛函微分方程和时滞微分方程等做了深入研究，并取得了一系列优秀的研究成果，如 [1] - [9]。在文献 [1] [2] [3] 和 [5] 等结果的启发下，通过建立了几个不同的Riccati变换函数和应用经典不等式确立了方程(E)的振动准则。并在几个前提下，获得了合理的结果，这是对文献中的一些结果进行了推广和改良。

引理1 [1] 如果 $x\left(t\right)$ 是方程的非振动解，且 $x\left(t\right)$ 是非负不为零的，则 $u\left(t\right)$ 只有以下两种情况：

1) $u\left(t\right)>0,u^{\prime }\left(t\right)>0,u^{″}\left(t\right)>0$；

2) $u\left(t\right)>0,u^{\prime }\left(t\right)<0,u^{″}\left(t\right)>0$。

证明：存在 $t_1\in \left[t_0,+\infty \right)$，设 $x\left(t\right)$ 为方程(E)在 $t\in \left[t_1,\infty \right)$ 上的一个非振动正解，根据方程(E)，有

$\left[r\left(t\right){\left|u^{″}\left(t\right)\right|}^{\theta -1}{u}^{″}\left(t\right)\right]\le -q\left(t\right)x^{\theta }\left(\tau \left(t\right)\right)<0$

设 $\Gamma \left(t\right)=r\left(t\right){\left|u^{″}\left(t\right)\right|}^{\theta -1}{u}^{″}\left(t\right)$，即有 $\Gamma \left(t\right)$ 是单调递减并且最终定号，可以判断 $u^{″}\left(t\right)>0$；否则，当 $t_2\in \left[t_1,\infty \right)$ 时，令 $t\in \left[t_2,\infty \right)$，若 $u^{″}\left(t\right)<0$，存在一个正数C，使得

$u^{\prime }\left(t\right)\le u^{\prime }\left(t_2\right)-C^{\frac{1}{\theta }}{\displaystyle {\int }_{t_2}^t\frac{1}{{\left(r\left(s\right)\right)}^{\frac{1}{\theta }}}\text{d}s}$

令 $k=u^{\prime }\left(t_2\right)$，则 $u\left(t\right)\le u\left(t_2\right)=k$，积分得

${\displaystyle {\int }_t^{t_2}{u}^{\prime }\left(s\right)\text{d}s}=-u\left(t\right)+u\left(t_2\right)<k\left(t_2-t\right)$

令 $t\to \infty$，则 $u\left(t\right)\to -\infty$，这与 $u\left(t\right)>0$ 矛盾，引理得证。

引理2 [9] 假设 $g\left(y\right)=By-A{y}^{\frac{\theta +1}{\theta }}$， $A>0$， $B>0$，则 $g\left(y\right)$ 当且仅当 $y_0={\left[\frac{B}{A}\right]}^{\theta }$ 处有最大值

$g\left(y_0\right)=\frac{{\theta }^{\theta }{B}^{\theta +1}}{{\left(\theta +1\right)}^{\theta +1}{A}^{\theta }}$

引理3 [3] 如果 $uf\left(u\right)>0$， $u\ne 0$，且 $\frac{f\left(u\right)}{u^{\theta }}\ge L>0$，则有

$\frac{f\left(u\right)}{u^{\theta }}\ge L>0,f\left(u\right)\ge L{u}^{\theta }$

引理4 [2] 存在 $t_1\in \left[t_0,+\infty \right)$，假设 $x\left(t\right)$ 为方程(E)在 $t\in \left[t_1,\infty \right)$ 上的一个非振动正解，满足 $u\left(t\right)>0$， $u^{\prime }\left(t\right)<0$， $u^{″}\left(t\right)>0$，且有

$\underset{t\to \infty }{\lim }\frac{1}{2}{\displaystyle {\int }_t^{+\infty }{L}^{\frac{1}{\theta }}{\displaystyle {\int }_{\mu }^{+\infty }{\left[\left(\frac{1}{r\left(v\right)}{\displaystyle {\int }_v^{+\infty }q\left(s\right)\text{d}s}\right)\right]}^{\frac{1}{\theta }}\text{d}v\text{d}\mu }}=\infty$

则有 $\underset{t\to \infty }{\lim }x\left(t\right)=0$。

引理5 [3] 若 $h\left(t\right)>0$， $h^{\prime }\left(t\right)>0$， $h^{″}\left(t\right)>0$， $h^{‴}\left(t\right)\le 0$，存在 $0<\beta <1$，使得

$\underset{t\to \infty }{\lim }\inf \frac{th\left(t\right)}{h^{\prime }\left(t\right)\beta t^2}\ge 1$

2. 主要结果

定理2.1 如果存在函数 $\phi \left(t\right)\in C^{rd}\left(\left[t_0,\infty \right),\left(0,\infty \right)\right)$， $\theta \ge 0$ 且 $\theta$ 为偶数与奇数商，满足

$\underset{t\to \infty }{\lim }\sup {\displaystyle {\int }_{t_0}^t\left[\frac{\phi \left(s\right)r^{\prime }\left(s\right)}{{\left(\Omega \left(s\right)\right)}^{\theta }{r}^2\left(s\right)}-\frac{{\left({\phi }^{\prime }\left(s\right)\right)}^{\frac{1}{\theta }+1}}{{\left(\theta +1\right)}^{\theta +1}{\left(\phi \left(s\right){\tau }^{\prime }\left(s\right)\right)}^{\theta }}\right]\text{d}s}=+\infty$ (1)

和

$\underset{t\to \infty }{\lim }\frac{1}{2}{\displaystyle {\int }_t^{+\infty }{L}^{\frac{1}{\theta }}{\displaystyle {\int }_{\mu }^{+\infty }{\left[\left(\frac{1}{r\left(v\right)}{\displaystyle {\int }_v^{+\infty }q\left(s\right)\text{d}s}\right)\right]}^{\frac{1}{\theta }}\text{d}v\text{d}\mu }}=\infty$ (2)

其中， $\Omega \left(t\right)$ 是正则的，则方程(E)是振动的或者 $x\left(t\right)$ 最终趋于0。

证明：不失一般性，存在 $t_1\in \left[t_0,+\infty \right)$，不妨设 $x\left(t\right)$ 为方程(E)在 $t\in \left[t_1,\infty \right)$ 上的一个非振动解且 $x\left(t\right)>0$，根据引理1可知只有两种情况。若满足 $u^{\prime }\left(t\right)>0$，则方程(E)取绝对值变成

${\left[r\left(t\right){\left(u^{″}\left(t\right)\right)}^{\theta }\right]}^{\prime }+q\left(t\right){\left(x\left(\tau \left(t\right)\right)\right)}^{\theta }=0$

这样有

$x\left(t\right)\ge \left(1-p\left(t\right)\right)u\left(t\right)$ (3)

由广义Riccati变换得

$R\left(t\right)=\phi \left(t\right)\frac{{\left(u^{″}\left(t\right)\right)}^{\theta }}{{\left(u^{\prime }\left(\tau \left(t\right)\right)\right)}^{\theta }}$ , $t\in \left[t_1,+\infty \right)$

根据求导性质可得

$R^{\prime }\left(t\right)=\frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}R\left(t\right)+\phi \left(t\right)\frac{\theta {\left(u^{″}\left(t\right)\right)}^{\theta -1}{u}^{‴}\left(t\right)}{{\left(u^{\prime }\left(\tau \left(t\right)\right)\right)}^{\theta }}-\phi \left(t\right)\frac{\theta {\left(u^{″}\left(t\right)\right)}^{\theta }{u}^{″}\left(\tau \left(t\right)\right){\tau }^{\prime }\left(t\right)}{{\left(u^{\prime }\left(\tau \left(t\right)\right)\right)}^{\theta +1}}$ .

因为 $u^{″}\left(\tau \left(t\right)\right)\ge u^{″}(t)$

$R^{\prime }\left(t\right)\le \frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}R\left(t\right)-\phi \left(t\right)\theta {\left(\frac{u^{″}\left(t\right)}{u^{\prime }\left(t\right)}\right)}^{\theta }\left(-\frac{u^{‴}\left(t\right)}{u^{″}\left(t\right)}\right)-\phi \left(t\right)\frac{\theta R{\left(t\right)}^{\frac{1}{\theta }+1}{\tau }^{\prime }\left(t\right)}{\phi {\left(t\right)}^{\frac{1}{\theta }}}$ (4)

因为 $r^{\prime }\left(t\right)u^{″}{\left(t\right)}^{\theta }+\theta r\left(t\right)u^{″}{\left(t\right)}^{\theta -1}{u}^{‴}\left(t\right)<0$，且有 $u^{″}\left(t\right)<0$，可得

$\frac{r^{\prime }\left(t\right)}{\theta r\left(t\right)}\le -\frac{u^{‴}\left(t\right)}{u^{″}(t)}$

令 $s>t$，则有

$\frac{r^{\frac{1}{\theta }}\left(t\right)u^{″}\left(t\right)}{r^{\frac{1}{\theta }}\left(s\right)}\ge u^{″}\left(s\right)$ (5)

在 $\left[t,l\right]\left(l\in \left[t_1,\infty \right)\right)$ 上对式(3)积分，且令 $l\to \infty$，有

$-\frac{u^{\prime }\left(t\right)}{u^{″}\left(t\right)}\le r^{\frac{1}{\theta }}\left(t\right)\Omega \left(t\right)$ (6)

将(5)和(6)代入(4)得

$R^{\prime }\left(t\right)\le \frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}R\left(t\right)-\phi \left(t\right)\frac{\theta R{\left(t\right)}^{\frac{1}{\theta }+1}{\tau }^{\prime }\left(t\right)}{{\phi }^{\frac{1}{\theta }}\left(t\right)}-\frac{\phi \left(t\right)r^{\prime }\left(t\right)}{{\left(\Omega \left(t\right)\right)}^{\theta }{r}^2\left(t\right)}$ (7)

由引理2得

$R^{\prime }\left(t\right)\le \frac{{\left({\phi }^{\prime }\left(t\right)\right)}^{\frac{1}{\theta }+1}}{{\left(\theta +1\right)}^{\theta +1}{\left(\phi \left(t\right){\tau }^{\prime }\left(t\right)\right)}^{\theta }}-\frac{\phi \left(t\right)r^{\prime }\left(t\right)}{{\left(\Omega \left(t\right)\right)}^{\theta }{r}^2(t)}$

对上式从 $\left[t_2,t\right]$ $\left(t_2\in \left[t_1,\infty \right)\right)$上对s积分，有

${\displaystyle {\int }_{t_2}^t\left[\frac{\phi \left(s\right)r^{\prime }\left(s\right)}{{\left(\Omega \left(s\right)\right)}^{\theta }{r}^2\left(s\right)}-\frac{{\left({\phi }^{\prime }\left(s\right)\right)}^{\frac{1}{\theta }+1}}{{\left(\theta +1\right)}^{\theta +1}{\left(\phi \left(s\right){\tau }^{\prime }\left(s\right)\right)}^{\theta }}\right]\text{d}s}\le R\left(t_2\right)-R\left(t\right)\le R\left(t_2\right)$ (8)

显然，式(8)与条件(1)矛盾；若 $u^{\prime }\left(t\right)$ 满足 $u^{\prime }\left(t\right)<0$ 情况，同理，由引理4可知， $x\left(t\right)$ 最终趋于0，定理得证。

定理2.2 如果存在函数 $\phi \left(t\right)\in C^{rd}\left(\left[t_0,\infty \right),\left(0,\infty \right)\right)$，满足

$\underset{t\to \infty }{\lim }\sup \left[\phi \left(s\right)q\left(s\right){\left(1-p\left(\tau \left(s\right)\right)\right)}^{\theta }{\left(\beta \tau \left(s\right)\right)}^{\theta }-\frac{{\phi }^{\prime }{\left(s\right)}^{\theta +1}r{\left(\tau \left(s\right)\right)}^{\theta +1}}{{\left(\theta +1\right)}^{\theta +1}{\left(r\left(s\right)\phi \left(s\right)\right)}^{\theta }}\right]\text{d}s=\infty$ (9)

和

$\underset{t\to \infty }{\lim }\frac{1}{2}{\displaystyle {\int }_t^{+\infty }{L}^{\frac{1}{\theta }}{\displaystyle {\int }_{\mu }^{+\infty }{\left[\left(\frac{1}{r\left(v\right)}{\displaystyle {\int }_v^{+\infty }q\left(s\right)\text{d}s}\right)\right]}^{\frac{1}{\theta }}\text{d}v\text{d}\mu }}=\infty$ (10)

其中， $\Omega \left(t\right)$ 是正则的， $\theta \ge 0$。

则方程(E)是振动的或者t趋于无穷时， $x\left(t\right)$ 极限为0。

证明：不失一般性，存在 $t_1\in \left[t_0,+\infty \right)$，不妨设方程(E)在 $\left[t_0,\infty \right)$ 上有一个非振动正解 $x\left(t\right)$，由引理1可知，只有两种情况. 若 $u^{\prime }\left(t\right)$ 最终为正数，则有

$x\left(t\right)\ge \left(1-p\left(t\right)\right)u\left(t\right)$ (11)

由广义Riccati变换得

$M\left(t\right)=\phi \left(t\right)\frac{r\left(t\right){\left(u^{″}\left(t\right)\right)}^{\theta }}{{\left(u^{\prime }\left(t\right)\right)}^{\theta }},t\in \left[t_0,+\infty \right)$

由求导法则及式(11)有

$M^{\prime }\left(t\right)\le \frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}M\left(t\right)-\phi \left(t\right)\frac{q\left(t\right){\left[\left(1-p\left(\tau \left(t\right)\right)\right)u\left(\tau \left(t\right)\right)\right]}^{\theta }}{{\left(u^{\prime }\left(\tau \left(t\right)\right)\right)}^{\theta }}-\phi \left(t\right)\frac{\theta r\left(t\right){\left(u^{″}\left(t\right)\right)}^{\theta +1}}{{\left(u^{\prime }\left(\tau \left(t\right)\right)\right)}^{\theta +1}}$ (12)

记 $h\left(t\right)=u\left(t\right)$，由引理5得， $t\ge t_0$，存在 $0<\beta <1$，使得

$\frac{u\left(t\right)}{u^{\prime }\left(t\right)}\ge \beta t$ (13)

由式(11)和式(12)，式(13)为

$\phi \left(t\right)q\left(t\right){\left[1-p\left(\tau \left(t\right)\right)\right]}^{\theta }{\left(\beta \tau \left(t\right)\right)}^{\theta }\le \frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}M\left(t\right)-\frac{\theta {\left(M\left(t\right)\right)}^{{}^{\frac{\theta +1}{\theta }}}}{{\left(r\left(t\right)\phi \left(t\right)\right)}^{\frac{1}{\theta }}}-M^{\prime }\left(t\right)$ (14)

令 $B=\frac{{\phi }^{\prime }\left(t\right)}{\phi \left(t\right)}$， $A=\frac{\theta }{{\left(r\left(t\right)\phi \left(t\right)\right)}^{\frac{1}{\theta }}}$，由引理2得

$\phi \left(t\right)q\left(t\right){\left[1-p\left(\tau \left(t\right)\right)\right]}^{\theta }{\left(\beta \tau \left(t\right)\right)}^{\theta }\le \frac{{\left(r\left(\tau \left(t\right)\right){\phi }^{\prime }\left(t\right)\right)}^{\theta +1}}{{\left(\theta +1\right)}^{\theta +1}{\left(r\left(t\right)\phi \left(t\right)\right)}^{\theta }}-M^{\prime }\left(t\right)$ (15)

对(15)两边积分得

$\begin{array}{l}{\displaystyle {\int }_{t_0}^t\left[\phi \left(s\right)q\left(s\right){\left[1-p\left(\tau \left(s\right)\right)\right]}^{\theta }{\left(\beta \tau \left(s\right)\right)}^{\theta }-\frac{{\left(r\left(\tau \left(s\right)\right){\phi }^{\prime }\left(s\right)\right)}^{\theta +1}}{{\left(\theta +1\right)}^{\theta +1}{\left(r\left(s\right)\phi \left(s\right)\right)}^{\theta }}\right]\text{d}s}\\ \le M\left(t_0\right)-M\left(t\right)\le M(t0)\end{array}$

所得结果与条件(9)矛盾。

若 $u^{\prime }\left(t\right)$ 最终小于零，由引理4可以得到 $x\left(t\right)$ 最终趋于0；因此，定理证明完毕。

3. 例子

例1考虑三阶微分方程

${\left(t{\left[{\left(x\left(t\right)+p_{0}x\left(\frac{t}{2}\right)\right)}^{\prime \text{}\prime }\right]}^2\right)}^{\prime }+t^3{x}^2\left(\frac{t}{3}\right)=0,t\ge t_0>0$ (16)

其中取 ${\phi }^{\prime }\left(t\right)=1$， $p\left(t\right)=p_0$，由(1)式得

$\underset{t\to \infty }{\lim }\left[\frac{\phi \left(t\right)r^{\prime }\left(t\right)}{{\left(\Omega \left(t\right)\right)}^{\theta }{r}^2\left(t\right)}-\frac{{\left({\phi }^{\prime }\left(t\right)\right)}^{\frac{1}{\theta }+1}}{{\left(\theta +1\right)}^{\theta +1}{\left(\phi \left(t\right){\tau }^{\prime }\left(t\right)\right)}^{\theta }}\right]=\underset{t\to \infty }{\lim }\left(t-\frac{1}{9t^{\frac{1}{2}}}\right)=\infty$

由(2)式得

$\underset{t\to \infty }{\lim }\frac{1}{2}{\displaystyle {\int }_t^{+\infty }{L}^{\frac{1}{2}}{\displaystyle {\int }_{\mu }^{+\infty }{\left[\left(\frac{1}{v}{\displaystyle {\int }_v^{+\infty }q\left(s\right)\text{d}s}\right)\right]}^{\frac{1}{2}}\text{d}v\text{d}\mu }}=\infty$

故方程(16)满足定理2.1，易证得方程(16)是振动的或者 $\underset{t\to \infty }{\lim }x\left(t\right)=0$。用文 [9] 的推论是不能证明本文

例3.1的。

例2考虑三阶微分方程

${\left(t^3{\left[{\left(x\left(t\right)+p_{0}x\left(\frac{t}{2}\right)\right)}^{\prime \text{}\prime }\right]}^{\frac{3}{2}}\right)}^{\prime }+t^3{x}^{\frac{3}{2}}\left(\frac{t}{3}\right)=0,t\ge t_0>0$ (17)

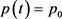其中 $\theta =\frac{3}{2}$， $\phi \left(t\right)=t$， ${\phi }^{\prime }\left(t\right)=1$， $q\left(t\right)=t^3$，，由式(9)得

由(10)式得

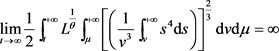
故方程(17)满足定理2.2，因此方程(17)是振动的或者，发现用定理2.1是判断不了方程(17)

的振动性质，但定理2.2是可以证明例1的。定理2.1比定理2.2的适用范围更小，限制为偶数与奇数商，定理2.2是把文 [2] 中定理1的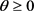是两个正奇数商推广到。

基金项目

1、广东石油化工学院理学院科研扶持基金重点项目(NO.: KY201801)；2、广东省创新创业培养项目；广东石油化工学院创新创业培养项目。

NOTES

^*通讯作者。