1. 引言
本文研究的图均为无向的简单图,且大多数术语均是标准的,可以在很多书本上看到,例如 [2],设
,其点集和边集分别为
和
,并
和
分别表示图G的阶数和边数。设
,
表示点v的邻点集合,
表示点v的度,并称v为一个
-点。用
表示t-点v的度序列,其中
为点v各个邻点的度。类似,
-点表示度数大于等于k的点。而
和
分别表示G的最大度和最小度。对
,我们记
,而
即为v在A中的邻点的个数。设
,记
为由S生成的G的支撑子图
。记长度为m的圈为
,记
阶星和N阶完全图分别为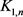 和
和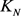 。
。
对于给定的图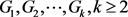 ,k-色Ramsey数
,k-色Ramsey数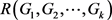 是最小的正整数p,使得对p阶完全图
是最小的正整数p,使得对p阶完全图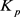 进行任意的k-边着色,总是存在某个着i色的单色图
进行任意的k-边着色,总是存在某个着i色的单色图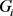 ,其中
,其中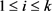 。如果
。如果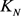 的一个k-边着色不包含任意i色的单色图
的一个k-边着色不包含任意i色的单色图 ,
,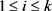 ,那么称
,那么称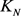 是可
是可 -边着色的,并将这种着色方案下的k-边着色完全图
-边着色的,并将这种着色方案下的k-边着色完全图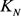 称为
称为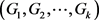 -图。设
-图。设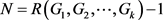 ,如果完全图
,如果完全图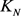 被赋予一个
被赋予一个 -边着色,那么称它为
-边着色,那么称它为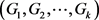 -Ramsey图。显然,它是相对于Ramsey数
-Ramsey图。显然,它是相对于Ramsey数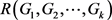 的一个极值图。类似的,如果图G的一个k-边着色不包含任意i色的单色图
的一个极值图。类似的,如果图G的一个k-边着色不包含任意i色的单色图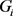 ,
,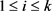 , 那么称G是可
, 那么称G是可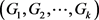 -边着色的。
-边着色的。
Ramsey数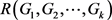 的确定是一个NP-Hard问题。至今,虽然关于2-色Ramsey数的研究结果比较丰富,精确值的确定也非常多,但涉及的图类相对比较少。至于3-色及3-色以上的k-色Ramsey数的研究结果目前并不多,精确值确定的图类更少而少之。对图类的Ramsey数研究方法比较常见的数学方法有概率方法 [3] [4] 和数学归纳 [5] [6]。概率方法一般是对于一些阶数较大的图给出相应的Ramsey数的上下界比较有效。数学归纳法一般用于Ramsey图成功构造的基础上进行的Ramsey数的确定,此时往往N阶起的Ramsey图用组合方法容易构造,但小阶图的构造还是要踏踏实实的,纯人工构造小图的极图需要大量的尝试且需要一定的运气,然而幸运往往不够,对此,需要借助计算机。例如,孙永奇等利用计算机和数学归纳法相结合的方法确定了
的确定是一个NP-Hard问题。至今,虽然关于2-色Ramsey数的研究结果比较丰富,精确值的确定也非常多,但涉及的图类相对比较少。至于3-色及3-色以上的k-色Ramsey数的研究结果目前并不多,精确值确定的图类更少而少之。对图类的Ramsey数研究方法比较常见的数学方法有概率方法 [3] [4] 和数学归纳 [5] [6]。概率方法一般是对于一些阶数较大的图给出相应的Ramsey数的上下界比较有效。数学归纳法一般用于Ramsey图成功构造的基础上进行的Ramsey数的确定,此时往往N阶起的Ramsey图用组合方法容易构造,但小阶图的构造还是要踏踏实实的,纯人工构造小图的极图需要大量的尝试且需要一定的运气,然而幸运往往不够,对此,需要借助计算机。例如,孙永奇等利用计算机和数学归纳法相结合的方法确定了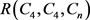 的值,可见文献 [6] [7] [8]。但是,一般情况我们确定一个Ramsey数
的值,可见文献 [6] [7] [8]。但是,一般情况我们确定一个Ramsey数 的确切值都很难,更不要提确定某些图类对应的Ramsey数,其原因很大程度上是我们遇到的图类其Ramsey图往往不能通过常规的组合方法得以成功构造。这时,对于阶数不大的图,我们可采用的方法:用数学方法对图的结构性质进行分析的基础上,再借助计算机帮助来构造需要的Ramsey图。
的确切值都很难,更不要提确定某些图类对应的Ramsey数,其原因很大程度上是我们遇到的图类其Ramsey图往往不能通过常规的组合方法得以成功构造。这时,对于阶数不大的图,我们可采用的方法:用数学方法对图的结构性质进行分析的基础上,再借助计算机帮助来构造需要的Ramsey图。
本论文我们仅关注若干3-色Ramsey数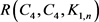 。为了方便,当我们考虑3-边着色图G时,默认其边被红蓝绿三色所着色。设
。为了方便,当我们考虑3-边着色图G时,默认其边被红蓝绿三色所着色。设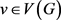 ,我们用
,我们用 ,
,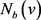 和
和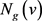 分别表示v通过红边,蓝边和绿边相邻的邻点集合,并且记
分别表示v通过红边,蓝边和绿边相邻的邻点集合,并且记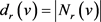 ,
,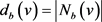 以及
以及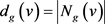 。设
。设 ,
,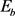 和
和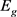 分别表示为红色,蓝色和绿色的边集合,当然
分别表示为红色,蓝色和绿色的边集合,当然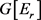 ,
,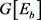 ,
, 分别表示由红边,蓝边,绿边导出的子图。
分别表示由红边,蓝边,绿边导出的子图。
2019年张雪梅等人不仅给出了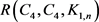 的一个一般的上界,而且,确定了某特殊类型n的Ramsey数
的一个一般的上界,而且,确定了某特殊类型n的Ramsey数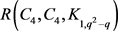 的精确值,可见文献 [1]。
的精确值,可见文献 [1]。
定理1 [1] 对所有的n,都有 。如果
。如果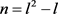 ,其中
,其中 ,那么
,那么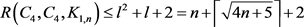 。
。
定理2 [1] 对所有的素数幂q,都有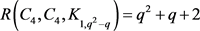 。
。
2-色Ramsey数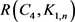 的研究要追溯到上世纪80年代,即使现在仍然是热点,但相应极值图的构造都尚未找到一般组合方法,至于3-色Ramsey数
的研究要追溯到上世纪80年代,即使现在仍然是热点,但相应极值图的构造都尚未找到一般组合方法,至于3-色Ramsey数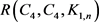 的极值图的构造就更没有一般组合方法。定理2证明中的极值图的构造用的是代数方法。除此之外,仅为当
的极值图的构造就更没有一般组合方法。定理2证明中的极值图的构造用的是代数方法。除此之外,仅为当 时(注意当
时(注意当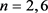 时为定理2的两个特例)
时为定理2的两个特例)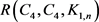 被确定,它们的极值图通过人工方法构造而得,可见文献 [1]。
被确定,它们的极值图通过人工方法构造而得,可见文献 [1]。
定理 3 [1]
在本文中,我们希望对小数n借助计算机寻找极值图,从而可以确定更多的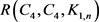 的值。我们所得结果如下:
的值。我们所得结果如下:
定理4 当 时,
时,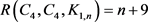 。
。
对于定理1中一般的上界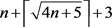 ,张雪梅等人仅找到
,张雪梅等人仅找到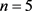 时
时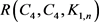 可以达该上界。由定理4,显然,当
可以达该上界。由定理4,显然,当 时,
时,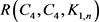 也取到该上界,再一次说明上界
也取到该上界,再一次说明上界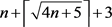 是紧的。
是紧的。
定理4的证明请参看本文的第3节,而第2节给出一些已知或易证引理,为定理[DL1]的证明做准备。
2. 一些引理
Turán数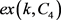 表示不包含
表示不包含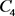 的k阶图能达到的最大边数。
的k阶图能达到的最大边数。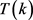 是由所有不包含
是由所有不包含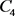 且边数最大即边数为
且边数最大即边数为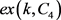 的k阶图全体组成的集合。众所周知,Reiman在1958年证明了
的k阶图全体组成的集合。众所周知,Reiman在1958年证明了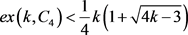 ,即给出了
,即给出了 的一个一般上界,可见文献 [9]。Turán数
的一个一般上界,可见文献 [9]。Turán数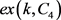 精确值的确定工作是非常艰巨的,即使对于小数k的情形。1989年Clapham等人确定了
精确值的确定工作是非常艰巨的,即使对于小数k的情形。1989年Clapham等人确定了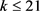 时
时 的值,并给出
的值,并给出 的刻画,可见文献 [10]。当然,到目前为止对于小数k已经有更多的
的刻画,可见文献 [10]。当然,到目前为止对于小数k已经有更多的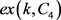 的值被确定。这里我们仅列出我们需要的
的值被确定。这里我们仅列出我们需要的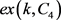 的值,以及
的值,以及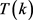 的情况。
的情况。
引理1 [10]
引理2 [10]
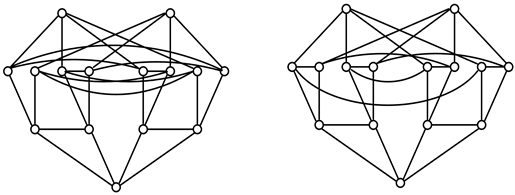
而且,T(15)中仅有2种非同构图,且均为4-正则图。另外,T(16)中仅有2种非同构图如图1所示,显然,T(16)中的图的所有5-点组成的集合恰为唯一的3-点的邻域。
 T(15)
T(15)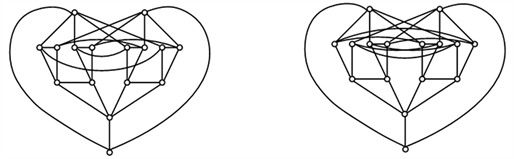 T(16)
T(16)
Figure 1. T(15), T(16): Graphs with the maximum number of edges without 4-cycles of order 15,16
图1. T(15), T(16):不含4-圈的边数最大15, 16阶图
2019年张雪梅等人给出了Turán数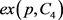 和Ramsey数
和Ramsey数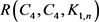 的一个关系,可见文献 [1],借助该关系我们确定定理4中Ramsey数的一个上界。
的一个关系,可见文献 [1],借助该关系我们确定定理4中Ramsey数的一个上界。
引理3 [1] 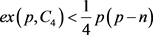 ,则
,则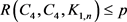 。
。
为了确定定理4中Ramsey数的一个下界,我们分析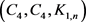 -图的结构性质时,还需要下面两个引理。
-图的结构性质时,还需要下面两个引理。
引理4 设红蓝黄3-边着色的完全图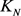 为
为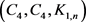 -图,则
-图,则
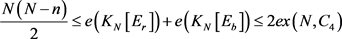 。
。
证明 因为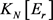 和
和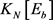 都不包含4-圈,所以
都不包含4-圈,所以 和
和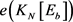 都不超过
都不超过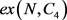 ,于是
,于是 。另一方面,因为
。另一方面,因为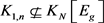 ,所以
,所以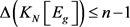 ,于是
,于是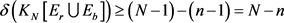 。因此,
。因此,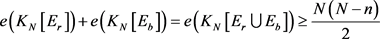 。 综上可知,
。 综上可知,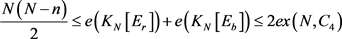 。 £
。 £
引理 5设G为不包含4-圈的图, 。则
。则
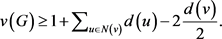 (1)
(1)
证明 对任意的 ,设
,设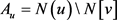 其中
其中 。因为
。因为 ,显然对任意
,显然对任意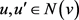 有
有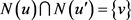 ,于是
,于是 。因此
。因此 以及
以及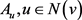 为
为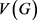 的一些不交子集。于是
的一些不交子集。于是
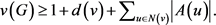 (2)
(2)
另外,由 ,显然对任意
,显然对任意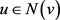 有
有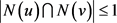 ,即
,即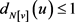 ,于是
,于是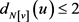 。而且,如果
。而且,如果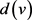 为奇数,即v为顶点集
为奇数,即v为顶点集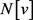 在G中的导出子图
在G中的导出子图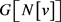 的一个奇度点,由于任意图的奇度点数必为偶数,故存在某
的一个奇度点,由于任意图的奇度点数必为偶数,故存在某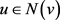 满足
满足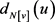 为奇数,从而该点满足
为奇数,从而该点满足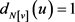 。因此对任意
。因此对任意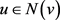 有
有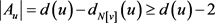 ,而且,如果
,而且,如果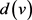 为奇数,存在某
为奇数,存在某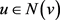 满足
满足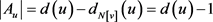 。于是,结合不等式(1),我们立即得到不等式(2)。 £
。于是,结合不等式(1),我们立即得到不等式(2)。 £
由引理5容易知道下列引理6成立。
引理 6设G为不包含4-圈的图,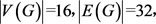 则G中有3-点和5-点,则3-点一定与5-点相邻。
则G中有3-点和5-点,则3-点一定与5-点相邻。
3. 主要结果的证明
定理1的证明:设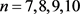 ,
,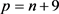 ,
,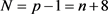 。
。
先证明 。由引理1可知
。由引理1可知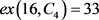 ,
,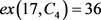 ,
,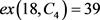 ,
,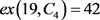 。容易验证
。容易验证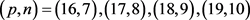 均满足不等式
均满足不等式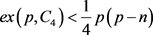 。于是,由引理3,
。于是,由引理3, 。
。
下面我们将证明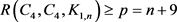 。为此,我们需要构造一个
。为此,我们需要构造一个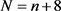 阶的
阶的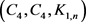 -图。换言之,我们将用红色,蓝色和绿色定义
-图。换言之,我们将用红色,蓝色和绿色定义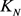 的一个3-边着色,使得
的一个3-边着色,使得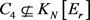 ,
,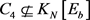 ,
,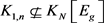 。在此,我们将借助计算机构造我们需要的Ramsey图。如果直接使用计算机构造,运行时间将会较长。我们采用的策略是在数学方法分析图结构的基础上利用计算机辅助构造Ramsey图,即先对
。在此,我们将借助计算机构造我们需要的Ramsey图。如果直接使用计算机构造,运行时间将会较长。我们采用的策略是在数学方法分析图结构的基础上利用计算机辅助构造Ramsey图,即先对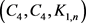 -边着色完全图
-边着色完全图 的结构进行分析,尽可能的确定
的结构进行分析,尽可能的确定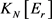 ,
,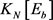 ,
, 的结构特性,比如边数,最大度等;然后使用计算机辅助我们寻找需要的Ramsey图。
的结构特性,比如边数,最大度等;然后使用计算机辅助我们寻找需要的Ramsey图。
设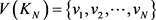 。我们将对完全图
。我们将对完全图 进行红蓝绿三色边着色:先依次用两个Lingo程序确定完全图
进行红蓝绿三色边着色:先依次用两个Lingo程序确定完全图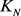 的红边集
的红边集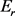 和蓝边集
和蓝边集 ,最后,剩余的边组成绿边集
,最后,剩余的边组成绿边集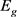 。Lingo程序1的目的:寻找红边集
。Lingo程序1的目的:寻找红边集 使得
使得 满足边数为
满足边数为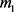 ,最大度为
,最大度为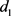 且不含4-圈的图。Lingo程序2的目的:在红边集的补集
且不含4-圈的图。Lingo程序2的目的:在红边集的补集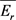 中寻找蓝边集
中寻找蓝边集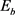 使得
使得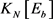 满足边数为
满足边数为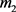 ,最大度为
,最大度为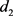 且不含4-圈的图。
且不含4-圈的图。
设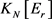 的邻接矩阵为X,其第i行第j列的元素为
的邻接矩阵为X,其第i行第j列的元素为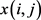 。
。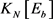 的邻接矩阵为Y,其第i行第j列的元素为
的邻接矩阵为Y,其第i行第j列的元素为 。于是,
。于是,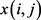 ,
,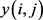 赋值如下:
赋值如下:
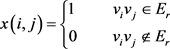
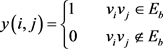
程序1
sets:
zb/1..N/;
link(zb,zb):X;
endsets
@for(link(i,j):x(i,j)=x(j,i));
@for(zb(i):x(i,i)=0);
@for(link:@bin(x));
@sum(link(i,j)|i \#lt\# j:x(i,j))=2m1;
@for(zb(i):@sum(zb(j):x(i,j))<=d1);
@for(link(i,j):@for(link(m,n)|~~i\#ne\#j\#~~and~~\#i\#ne\#m\#~~and~~\#i\#ne\#n\#~~and~~\#j\#ne\#m\#~~and~~\#j\#ne\#n\#~~and~~\#m\#ne\#n: x(i,j)+x(j,m)+x(m,n)+x(i,n)<=3;x(i,j)+x(j,n)+x(n,m)+x(m,i)<=3;x(i,m)+x(m,j)+x(j,n)+x(n,i)<=3));
根据程序1输出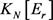 的邻接矩阵X。如果在程序1的结果中
的邻接矩阵X。如果在程序1的结果中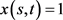 ,那么在程序2中限制
,那么在程序2中限制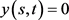 。
。
程序2
sets:
zb/1..N/;
link(zb,zb):Y;
endsets
@for(link(i,j):y(i,j)=y(j,i));
@for(zb(i):y(i,i)=0);
@for(link:@bin(y));
@sum(link(i,j)|i \#lt\# j:y(i,j))=2m2;
@for(zb(i):@sum(zb(j):y(i,j))<=d2);
@for(link(i,j):@for(link(m,n)|~~i\#ne\#j\#~~and~~\#i\#ne\#m\#~~and~~\#i\#ne\#n\#~~and~~\#j\#ne\#m\#~~and~~\#j\#ne\#n\#~~and~~\#m\#ne\#n: y(i,j)+y(j,m)+y(m,n)+y(i,n)<=3;y(i,j)+y(j,n)+y(n,m)+y(m,i)<=3;y(i,m)+y(m,j)+y(j,n)+y(n,i)<=3));
y(s,t)=0;
根据程序2输出 的邻接矩阵Y。
的邻接矩阵Y。
设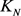 为一个红蓝绿3-边着色的完全图。如果
为一个红蓝绿3-边着色的完全图。如果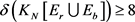 ,那么
,那么 ,所以
,所以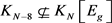 。反之亦然。于是,下面断言是显然。
。反之亦然。于是,下面断言是显然。
断言1 设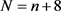 ,
,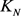 是一个依次经过程序1和程序2获得红蓝绿3-边着色的完全图。则
是一个依次经过程序1和程序2获得红蓝绿3-边着色的完全图。则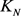 是一个
是一个 -完全图的充分必要条件是
-完全图的充分必要条件是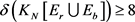 。
。
下面,对于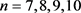 ,我们将依次分析相应
,我们将依次分析相应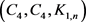 -完全图
-完全图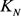 中
中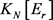 和
和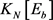 的结构性质。根据文献,对
的结构性质。根据文献,对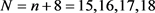 ,不含4-圈且边数最大的图的全体集合
,不含4-圈且边数最大的图的全体集合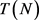 是完全确定的。因此,在分析
是完全确定的。因此,在分析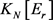 和
和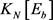 的结构时,先分析它们是否可以属于
的结构时,先分析它们是否可以属于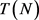 。也就是说,根据
。也就是说,根据 和
和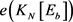 的值,将从大到小分情况进行讨论
的值,将从大到小分情况进行讨论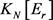 和
和 应具备的结构性质。最终,在结构分析的基础上,利用计算机程序1和程序2成功构建所需的N阶
应具备的结构性质。最终,在结构分析的基础上,利用计算机程序1和程序2成功构建所需的N阶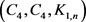 -完全图。
-完全图。
情形1. 当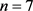 时,
时,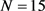 。由引理1和引理4可知
。由引理1和引理4可知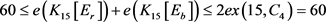 ,显然,
,显然,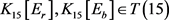 。由引理2,
。由引理2, 均为15阶的4-正则图。我们使用Lingo程序1和程序2可寻找到不含4-圈的4-正则图,
均为15阶的4-正则图。我们使用Lingo程序1和程序2可寻找到不含4-圈的4-正则图,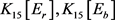 ,如图2所示。显然,
,如图2所示。显然,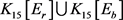 是一个8-正则图。由断言1,我们获得一个15阶
是一个8-正则图。由断言1,我们获得一个15阶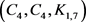 -完全图。因此,
-完全图。因此, 。
。
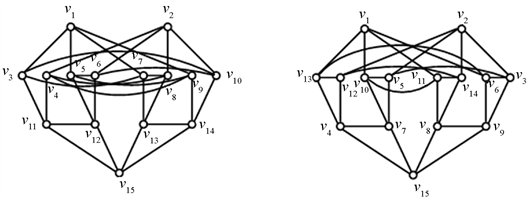
Figure 2.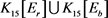 : A 8-regular graph of 15 order with edge coloring
: A 8-regular graph of 15 order with edge coloring
图2.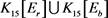 :一个15阶可
:一个15阶可 -边着色的8-正则图
-边着色的8-正则图
情形2. 当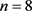 时,
时, 。由引理1和引理4可知
。由引理1和引理4可知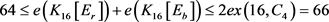 。
。
情形2.1. 假设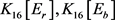 中存在之一属于
中存在之一属于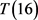 ,不妨设
,不妨设 。由引理2,
。由引理2,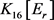 中有3个5-点,1个3-点,其余点均为4-点,而且唯一3-点的邻域恰好为5-点组成的集合。不妨令
中有3个5-点,1个3-点,其余点均为4-点,而且唯一3-点的邻域恰好为5-点组成的集合。不妨令 ,
,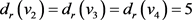 且
且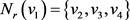 。因此,
。因此,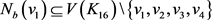 ,即在
,即在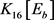 中
中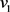 的任意邻点u都满足
的任意邻点u都满足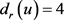 。于是,由
。于是,由 (参看断言1)知,
(参看断言1)知,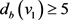 且点
且点 在
在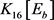 中所有邻点的度 ≥ 4。由引理5,
中所有邻点的度 ≥ 4。由引理5,
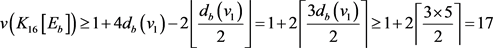 ,与
,与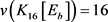 矛盾。
矛盾。
情形2.2. 设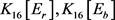 都不属于
都不属于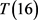 ,此时
,此时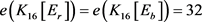 。显然
。显然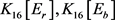 的平均度皆为4。再结合引理1知,此时
的平均度皆为4。再结合引理1知,此时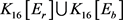 是一个8-正则图。
是一个8-正则图。
假设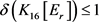 。不妨令v为
。不妨令v为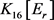 的最小度点。于是,
的最小度点。于是,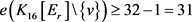 。也就是说,我们得到一个不包含4-圈且边数大于等于31的15阶图,与引理5中
。也就是说,我们得到一个不包含4-圈且边数大于等于31的15阶图,与引理5中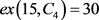 矛盾。
矛盾。
假设 。不妨设
。不妨设 为
为 的最小度点,即
的最小度点,即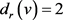 。于是,
。于是,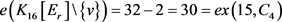 。所以,
。所以,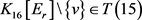 ,由引理2,
,由引理2, 是一个4-正则图。因此
是一个4-正则图。因此 中有1个2-点,2个5-点,其他点均4-点。又因为
中有1个2-点,2个5-点,其他点均4-点。又因为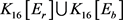 是一个8-正则图,故
是一个8-正则图,故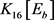 中有1个6-点,2个3-点,其他点均4-点。于是,v满足
中有1个6-点,2个3-点,其他点均4-点。于是,v满足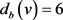 且在
且在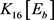 中的度序列为
中的度序列为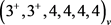 。由引理5,
。由引理5,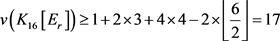 ,与
,与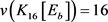 矛盾。
矛盾。
设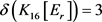 。假设
。假设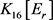 中仅有1个3-点,由
中仅有1个3-点,由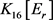 的平均度皆为4,此时
的平均度皆为4,此时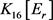 中有1个3-点,1个5-点,其他点均4-点。不妨令
中有1个3-点,1个5-点,其他点均4-点。不妨令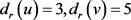 。由引理6,
。由引理6, 。否则,5-点v的每个邻点的度都为4。由引理5,
。否则,5-点v的每个邻点的度都为4。由引理5,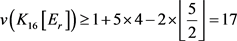 ,与
,与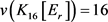 矛盾。另一方面,由
矛盾。另一方面,由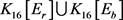 是一个8-正则图,此时
是一个8-正则图,此时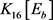 中有3-点v,5-点u,其他点均4-点。同理有
中有3-点v,5-点u,其他点均4-点。同理有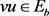 。故而
。故而 。矛盾!
。矛盾!
因此,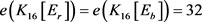 ,
, 是一个8正则图,
是一个8正则图,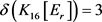 且
且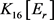 中至少有2个3-点。在此条件下,根据Lingo程序1和Lingo程序2构造图
中至少有2个3-点。在此条件下,根据Lingo程序1和Lingo程序2构造图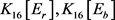 如图3所示。由断言1,我们获得一个16阶
如图3所示。由断言1,我们获得一个16阶 -完全图。因此,
-完全图。因此, 。
。
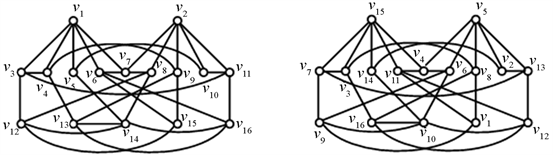
Figure 3.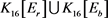 : A 8-regular graph of 16 order with edge coloring
: A 8-regular graph of 16 order with edge coloring
图3. :一个16阶可
:一个16阶可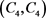 -边着色的8-正则图
-边着色的8-正则图
情形3. 当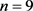 时,
时, 。由引理1和引理4可知
。由引理1和引理4可知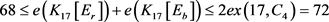 。
。
设 ,即
,即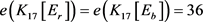 。由引理2,可知
。由引理2,可知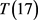 只有一种结构。见图4,根据Lingo程序1和程序2构造同构图
只有一种结构。见图4,根据Lingo程序1和程序2构造同构图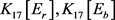 如图5所示。
如图5所示。
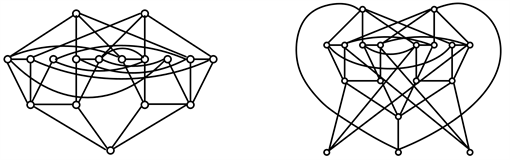 T(17) T(18)
T(17) T(18)
Figure 4. T(17), T(18): Graphs with the maximum number of edges without 4-cycles of order 17 and 18
图4. T(17), T(18): 不含4-圈的边数最大的17阶图和18阶图
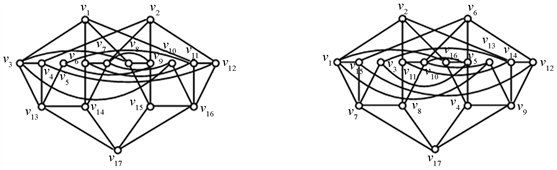
Figure 5.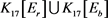 : A graph of 17 order with edge coloring
: A graph of 17 order with edge coloring
图5.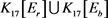 :一个17阶可
:一个17阶可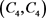 -边着色的图
-边着色的图
根据图5可以列出点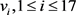 分别在
分别在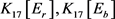 中的度,如表1所示。易检验每点
中的度,如表1所示。易检验每点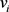 满足
满足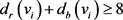 ,由断言1,我们获得一个17阶
,由断言1,我们获得一个17阶 -完全图。因此,
-完全图。因此,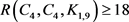 。
。
情形4. 当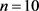 时,
时, 。由引理1和引理4可知
。由引理1和引理4可知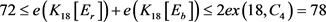 。
。
设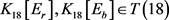 ,即
,即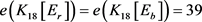 。由引理2可知
。由引理2可知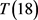 只有一种结构。根据Lingo程序1和程序2构造同构图
只有一种结构。根据Lingo程序1和程序2构造同构图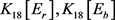 如图6所示。根据图6可以列出点
如图6所示。根据图6可以列出点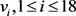 分别在
分别在 中的度,如表2所示。易检验每点
中的度,如表2所示。易检验每点 满足
满足 ,由断言1,我们获得一个18阶
,由断言1,我们获得一个18阶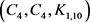 -完全图。因此,
-完全图。因此,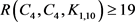 。
。
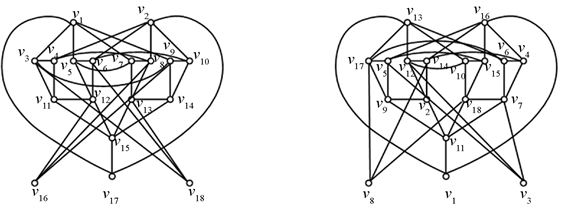
Figure 6.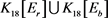 : A graph of 18 order with edge coloring
: A graph of 18 order with edge coloring
图6.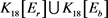 :一个18阶可
:一个18阶可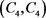 -边着色的图
-边着色的图
综上可知,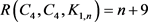 ,其中
,其中 。 £
。 £
致谢
该文作者受国家自然科学基金项目11801520资助。