1. 引言
场代数是顶点代数概念的“非局部性”推广。在顶点代数的定义中,局部性是一个基本的条件,把它换成较弱的结合性条件,将得到一个新的代数结构——场代数。由于场代数与顶点代数之间有着如此密切的联系,对场代数的研究将有助于更好的理解顶点代数及其相关领域。
在文献 [1] 中,作者系统讨论了态场对应、场代数的定义及初等性质,并且研究了场代数和顶点代数之间的关系,研究了态场对应的弱局部性和莱布尼兹共形代数上的张量代数等等。文献 [2] 研究了场代数的结合性,文献 [3] 和 [4] 分别引进了局部共形场代数和全场代数。本文将在上述文献给出的基本概念的基础上,探讨弱局部性与非局部性之间的关系,并给出具体实例加以说明。另外,本文对场代数的商空间也进行了描述,并讨论了一些基本性质。
本文假设所讨论的向量空间与各种代数结构都是指某个固定的域F上的,F可以是一般的域,必要时还可以假定它是复数域,从而保障线性变换特征值与特征向量的存在性。关于顶点代数的系统讨论,以及本文用到的一些术语与记号,参见文献 [5] [6] [7] [8] [9]。
设V是一个向量空间,
,若有线性映射:
及自同态
,使得下列条件成立:
1) 真空性
,
,其中
是恒等变换;
2) 平移不变性
(称T是V上的平移算子);
则称三元组
是态场对应。
进一步,若态场对应
满足结合性公理:对
,有
则称三元组
为场代数。
2. 预备知识
定义2.1 [1]:对
,若有正整数N,使得
,则称二元对
是N-弱局部的。若对充分大的N,总有
,则称二元对
是弱局部的。
定义2.2 [5]:(局部性)对
,若存在自然数
,使得下列等式成立:
其中
,则称
是相互局部的。
定义2.3 [1]:设V是场代数,I是V的子空间,且
。若有
,
,则称I是V的一个左理想。如果有
,
,则称I是V的一个右理想。若I既是左理想又是右理想,则I是V的一个双边理想。
3. 主要结果及证明过程
设V是域F上的向量空间,定义V上的算子向量空间
其加法和数乘运算都是自然定义的。称
是向量空间V上的场空间,其中的元素
为V上的场或算子。定义
上的双线性n-运算如下:
此时,
是F上的非结合代数,其中的算子也称为是下方截断的,见文献 [1]。
引理3.1:定义算子
,使得
的系数
与
的任何系数可交换,则有
。此时,算子
是N-弱局部的。
进一步,若还有
,则算子
是弱局部的。
证明:设
,其中
。根据引理的条件,有下列等式:
即,等式
成立,算子
是N-弱局部的。
定理3.2:设算子
,
如上,且
是下方截断的。若有正整数
使得
,
,且算子
满足条件:对任意的正整数
,存在非负整数n,使得系数
与
不可交换,则
不是局部的。
证明:对任意正整数
,要证明
。根据前面的计算式,只要证明
选取
,上述不等式化简为
。再根据定理条件:
与
不可交换,前面的不等式确实成立,从而算子
不是局部的。
注记:上述定理中的
不具有下方截断性。若要求
满足下方截断性,可选取正整数
,使得
,且
。此时,对任意的正整数
及整数k,满足:
,使得
,且
,这里
。取
,使它与
不可交换。再令
,则有下列式子:
从而有
因此,算子
不是局部的。
下面我们以二阶矩阵为例,给出一个具体的例子。
例3.3:1) 构造算子
:当
时,
为任意矩阵。当
时,令
。当
,令
。当
,令
。2) 构造算子
:当
时,
为任意矩阵。当
时,
,
或者
。当
时,
。此时,
。因此,
是
-弱局部的,但是它们不是局部的。
讨论算子的弱局部性是为了构造场代数,而局部性的研究是顶点代数要面临的问题。下面的例子给出了一些说明,其详细讨论见文献 [1] 和文献 [8]。
例3.4:设子空间W是向量空间
的一个弱局部子空间,它包含恒等变换
,且对n运算封闭,则
是一个态场对应。这里线性映射
定义如下:
其中
定义如上。若
满足结合性公理,则它是场代数。若还满足弱局部性,则它是强场代数。
引理3.5:设
是场代数,I是V的T不变的双边真理想,则
也是一个场代数。相应的线性映射可以如下给出:
证明:1) 合理性:商空间
中的n运算定义为:
。若
,
,则
,I是V的双边理想,必有
。
于是,
,运算的定义是合理的。
2) 真空性:
,
,其中
是恒等变换。
3) 平移不变性:
,T是
上的平移算子。
4) 因为
是场代数,对所有的
,有下列结合性等式:
将上式变形,得到下列等式:
对商空间
中的任意元素
,必有
故
也是一个场代数。
可以按照通常的方式定义场代数的同态,并且同态的核是理想,同态的像是场代数。
引理3.6:场代数的同态基本定理:设
是场代数
之间的同态,I是V的一个理想,并且
,则有唯一的场代数同态
,使得
。这里
是典范同态,而
。
特别,若
,则
是单射,此时
是同构。
证明:

1) 令
。映射
定义合理:若
,即
,
,有
。
,
。
2)
是同态:
。首先,它是向量空间的线性映。另外,它保持n运算:
3) 由
的定义直接看出:
。
4) 唯一性:若还有另外一个同态
,使得
。则
。即
。由此可知,
。
5)
是双射:由定义直接看出。因此,
是场代数的同构映射。
引理3.7:设
是场代数,I是V的真理想,则商代数
的理想构成的集合B与V包含I的理想构成的集合A之间有一一对应。特别地,
的理想形如
,这里L是V的包含I的理想。
证明:考虑典范态场对应同态
,由此定义集合之间的映射
1)
是单射:设理想
,且
。
,必有 。故存在
。故存在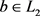 ,使得
,使得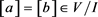 。于是
。于是 ,从而
,从而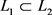 ,同理可得
,同理可得 ,则
,则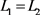 。
。
2) 是满射:设
是满射:设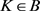 ,令
,令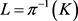 ,现证
,现证 。
。 ,
,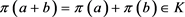 。从而
。从而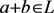 。
。 ,则
,则 ,同理可证
,同理可证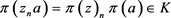 。因此,L是V的理想。另外,L是V的包含I的理想,即
。因此,L是V的理想。另外,L是V的包含I的理想,即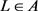 。最后由于典范映射
。最后由于典范映射 是满射,必有
是满射,必有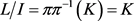 ,即
,即 是满射。
是满射。
因此, 是双射,引理结论成立。
是双射,引理结论成立。
引理3.8:设 是场代数,其中I,J为场代数
是场代数,其中I,J为场代数 的两个双边真理想,且有理想的包含关系:
的两个双边真理想,且有理想的包含关系: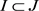 ,则有场代数之间的同构映射:
,则有场代数之间的同构映射: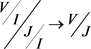 。
。
证明:由双边理想的定义可以验证 是
是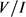 的双边理想,利用同态基本定理可以验证引理的结论成立。
的双边理想,利用同态基本定理可以验证引理的结论成立。