1. 引言
在现代化战场中,雷达探测起着至关重要的作用 [1]。同理,雷达为提高自身生存能力也要尽可能的降低被探测到的风险 [2]。反雷达探测又可以称作隐身技术,而表示目标隐身效果强弱的物理量被称作目标对电磁波的雷达截面(Radar Cross Section) [3]。RCS是基于平面波照射状态下目标各向同性散射的概念,降低雷达截面可以大大减少雷达探测作用,而频率选择表面可以实现这种效果。
由此提出FSS实现隐身天线罩,在我方雷达工作频段保证电磁波的自由通透,而在非工作频段实现高反射 [4] [5] [6]。对于有限大尺寸FSS甚至是曲面FSS的研究才是对FSS的有效扩充,找到高效建立应用FSS模型并快速分析应用FSS的传输特性是目前重要的研究领域 [7] [8] [9] [10]。在实际运用中曲面天线罩体因其表面不能完全展开成平面,导致单元不能像无限大平面模型一样严格周期分布,其效果也就产生了变化,所以FSS单元排布设计对天线罩起到了至关重要的影响 [11] [12],针对该问题本文研究了单元排布对曲面FSS天线罩传输特性的影响。
2. 单元设计与仿真
本文以实际工程为背景设计了圆环形单元结构,周期为10 mm × 10 mm正方形排布,工作中心频点为10 GHz。该单元由三层结构构成,基底陶瓷(天线罩)介电常数为3.5、厚度为9 mm,中间层为粘合胶体介电常数为3、厚度为0.025 mm,上层为金属板、厚度为0.025 mm,具体尺寸如图1(a)~(b)所示。文中使用的仿真软件为EastFDTD,是一款基于时域有限差分算法的光电磁实时仿真模拟软件,广泛用于各种电磁系统(天线/雷达、雷达罩、暗室、RCS、探测、加热等)和光电系统(如激光、LED、光纤等)等行业的仿真,与国际软件相比,在计算速度、精确度和电磁材料等方面,具有特殊的技术优势。
以该单元为周期结构,仿真其在无限大平面下的透过率曲线,分别以入射角和极化角为变量,观察随着角度的变化模型工作频点的变化规律:图1(c)为TE模极化角固定,入射角变化时对工作频点的影响,当入射角由0增加至80˚时,透过率仿真曲线的工作中心频点逐渐增大,有向高频段移动的趋势;图1(d)为入射角固定在70˚ (因为直锥模型的角度设置,在此选择固定入射角为70˚),极化角变化时对工作频点的影响,当极化角由0增加至90˚时,透过率仿真曲线的工作频点基本不变,说明该单元结构极化不敏感,且入射角70˚时各个极化角下单元的工作频点均处在10 GHz,透过率也基本处在90%以上。
 (a) (b)
(a) (b)  (c)
(c) 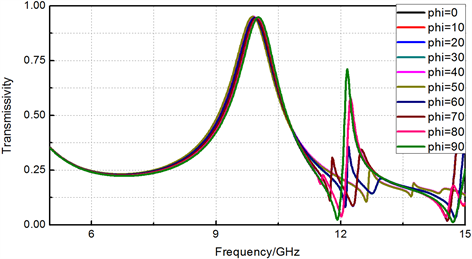 (d)
(d)
Figure 1. (a) (b) Elevation and side views of the unit structure, unit(mm); (c) Transmittance curve of the unit model when the polarization angle is fixed and the incidence angle is changed; (d) Transmittance curve of the unit model when the incidence angle of the fixed polarization angle changes
图1. (a) (b) 单元结构的正视图和侧视图,单位(mm);(c) 极化角固定入射角变化时,单元模型的透过率曲线;(d) 入射角固定极化角变化时,单元模型的透过率曲线
3. 天线罩的仿真与分析
3.1. 无FSS加成的天线罩
如图2所示天线罩模型通过在二维平面x-o-y内的直线绕x轴旋转得到,其中直线方程为y = x*tan20˚,锥体顶角20˚。天线罩厚度为9 mm,介电常数为3.5。

Figure 2. A three-dimensional schematic of the radome (unit: mm)
图2. 天线罩的三维示意图(单位:mm)
3.2. 平面FSS排布与仿真
排布一如图3(a):严格的正方排布:在锥体的扇形展开面上按照严格的正方周期将FSS单元一一排列,然后将扇面进行卷曲得到直锥,为保证单元的完整性,如果遇到边界处无法排列一个完整单元的位置,则不在该处放置单元。排布二如图3(b):初步优化排布,沿x轴每隔10 mm在罩体径向进行单元排布,单元周期不变且保证完整性,罩体表面将出现较小的空缺,虽然径向上形成周期排布但母线方向无序。排布三如图3(c):再优化排布,针对前一步中径向上每一圈的周长调整单元周期大小,做到径向严格周期排布消除空缺。仿真扇面模型工作波段,10 GHz的工作频点包含在其工作频段内。如图3(d)所示在5~15 GHz频段内,排布一模型的工作曲线与单一单元结构相同,排布二模型的工作频带杂乱峰值相对更高,排布三的工作频带更稳定峰值相对较低。对于有限大平面模型,无论排布二还是排布三都不是严格的周期排布,所以与排布一相比透过率曲线变化很大。
 (a)
(a)  (b)
(b)  (c)
(c) (d)
(d)
Figure 3. (a)~(c) The straight cone model is developed into a schematic diagram of plane fan, which is arranged one, two and three respectively in order; (d) Transmittance curves of three models in 5 - 15 GHz
图3. (a)~(c)直锥模型展开为平面扇形的示意图,按顺序分别对应排布一、二、三;(d) 在5~15 GHz内三种排布模型的透过率曲线
3.3. 直锥模型的FSS排布
将平面扇形模型进行卷曲得到最后的锥形FSS天线罩,需要将FSS单元结构排布在天线罩表面,首先沿x轴方向从x = 20到110处每隔10放置一个单元,再将单元绕x轴按一定角度旋转并复制,则在该处构成一圈排布的FSS,总计排布十圈。排布中所需要的坐标,旋角等数据通过Matlab程序计算得出,根据数据在仿真软件中构建模型如图4所示。排布三中,仅对单元周期进行了修改而单元的其他数据并未变化,故排布二中使用Matlab程序得到的排布数据仍然可以利用。用每一圈的周长去除以取整后每一圈排列的个数,得到了新的旋角、新的周期大小,由于周期改变量较小,故忽略周期对仿真结果的影响。
3.4. 直锥模型的FSS仿真数据
通过平面扇形模型曲线可以看出,FSS的工作频带在9~11 GHz,非工作频带为5~9 GHz、11~15 GHz,故在对锥体模型仿真时,添加带内频点的监视器:10 GHZ,带外频点的监视器:7、13 GHZ。由于排布一和排布二的直锥模型有缺陷,三种FSS排布的天线罩模型在进行数据分析时将对缺陷部分和非缺陷部分分别进行讨论。
3.4.1. 缺陷部分的讨论
不同频点下排布一模型、排布二模型和排布三模型的RCS仿真结果如图5所示。图5(a)中在7 GHz下,排布一模型和排布三模型的散射曲线在100˚时开始有明显的下降,且排布三模型在135˚附近有一个非常低的散射抑制。因此在带外7 GHz排布三模型的效果是最好的,因为排布三模型在一定程度上消除了缺陷对电磁波传输的影响。图5(b)中在10 GHz下,三种排布的散射效果相差不大。图5(c)中在13 GHz下,排布一模型和排布三模型的散射曲线整体要比排布二模型的散射曲线更低。在缺陷部分的对比中,排布三具有无缺陷的优势,工作频带内的散射效果与排布一、二相当,但工作频带外压制电磁波的效果最好。
 (a) (b)
(a) (b) (c)
(c)
Figure 5. Electromagnetic wave scattering curves of three kinds of models at different frequencies in defect section, (a) is the electromagnetic wave scattering curve at 7 GHz; (b) is the electromagnetic wave scattering curve at 10 GHz; (c) is the electromagnetic wave scattering curve at 13 GHz
图5. 缺陷部分不同频点下三种排布模型的电磁波散射曲线,(a) 为7 GHz下的电磁波散射曲线;(b) 为10 GHz下的电磁波散射曲线;(c) 为13 GHz下的电磁波散射曲线
3.4.2. 非缺陷部分的讨论
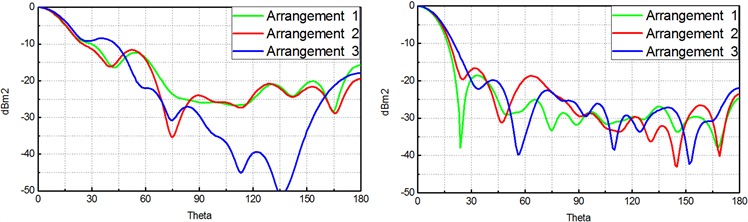
不同频点下三种排布方式的直锥模型RCS仿真结果如图6所示。图6(a)中在7 GHz下,排布三模型从85˚到160˚有一个非常明显的电磁散射压制,而排布一模型和排布二模型的曲线基本一致。图6(b)中在10 GHz下,三种排布模型的RCS曲线非常接近,其工作效果基本一致。图6(c)中在13 GHz下,从55˚到165˚之间,排布三模型的RCS曲线一直处于比较低的水平,说明在带外排布三模型对电磁波的压制效果最好。
通过对三种排布模型的缺陷部分和非缺陷部分的仿真结果对比和分析之后,发现在工作频带内排布三模型的效果和排布一、二模型相当,但在在工作频带外排布三对电磁散射的压制最好,说明这种优化后的排布方式更好的实现了工作频段电磁波的通透,非工作频段的高反射,采用这种消除缺陷排布的天线罩的实际应用效果会更好。
3.5. 小结
对天线罩表面的FSS从简单的正方形周期排布(排布一)到初布优化排布(排布二)到再优化排布(排布三),使用了圆环形单元进行仿真,排布一和二中单元交合处的缺陷在实际的运用中经常遇到,针对这个问题提出了排布三的优化办法,略微改变锥体上每圈单元的周期,使其能合理排布以消除缺陷的出现。
 (a) (b)
(a) (b) (c)
(c)
Figure 6. Electromagnetic wave scattering curves of three kinds of models at different frequencies in the non-defective section, (a) is the electromagnetic wave scattering curve at 7 GHz; (b) is the electromagnetic wave scattering curve at 10 GHz; (c) is the electromagnetic wave scattering curve at 13 GHz
图6. 非缺陷部分不同频点下三种排布模型的电磁波散射曲线,(a) 为7 GHz下的电磁波散射曲线;(b) 为10 GHz下的电磁波散射曲线;(c) 为13 GHz下的电磁波散射曲线
在数据分析中可以看出,FSS在罩体表面起到在工作频段电磁波的通透,非工作频段的高反射的作用,最关键的是在缺陷处排布三的FSS效果优于排布一和二的FSS,说明了这种优化排布想法的可行性,说明了不同FSS的排布方式对天线罩电磁波散射有不同的影响,但与设想中全面优于、明显优于的结果有所差距,这将作为下一步更高优化的方向。
4. 总结
本文考虑到FSS在实际运用中不能像在平面一样严格周期排布,提出了FSS排布方式对罩体散射的影响。本文构建了三个模型:正方形周期排布FSS的天线罩、初步优化排布FSS的天线罩和再优化排布FSS的天线罩,对比观察影响。
结果说明优化后的排布可以解决缺陷问题,并产生了一定的优化影响,实现了工作频段电磁波的通透非工作频段的高反射,但效果并没有预想的明显。原因是本文仅考虑了平行于锥体底面的、位于锥体表面的每一圈上的单元周期化排布,而对于锥体母线方向上单元的周期化未进行处理,从而导致整体的周期化不完善,故优化结果没有特别显著。在后续的研究中,对经线方向和纬线方向同时设计优化,可作为一个研究方向。
基金项目
长春理工大学校青年基金(XQNJJ-2017-03);吉林省科技计划项目(20170312024, 20190201013);国家自然科学基金(61405189)。