一种数据融合的乳腺癌分类模型

A Data Fusion Model of Breast Cancer Classify Cation

摘要: 针对乳腺癌智能诊断中的分类器欠稳定，样本分布适应性差等问题。本文提出一种基于Adaboost集成BP、RBF及Naïve Bayess三网的分类器构建算法。首先，采用三种不同的分类算法训练出不同的弱分类器；然后，通过权重在分配策略，增加患病样本被错分健康样本的权重，减小健康样本被错分的患病样本的权重；最后，通过调整后的权重重组弱分类器，达到构成一种强分类器。利用UCI (University of California, Irvine)数据库中的威斯康星乳腺癌数据进行算法对比验证，实验结果表明：本文所提出分类模型优于单一算法。

Abstract: In the intelligent diagnosis of breast cancer, the classifier is not stable and the sample distribution adaptability is poor. This paper proposes a classifier construction algorithm based on AdaBoost ensemble BP, RBF and Naïve Bayes. First, three different classification algorithms are used to train different weak classifiers. Then, by means of weight redistribution strategy, the weight of the diseased samples in which are misclassified is increased and reduces the weight of healthy samples misclassified to diseased samples. Finally, a strong classifier is constructed by reorganizing the weak classifier with the adjusted weights. The comparison and verification of the algorithm based on the Wisconsin breast cancer data in UCI database show that the proposed classification model is superior to the single algorithm.

1. 引言

近期，根据全球癌症统计数据，乳腺癌仍然是导致女性死亡的主要原因之一，每年新增病例大约有24.2% (210万)，死亡病例有626,697例 [1]。调查表明准确的早期检查，癌症患者存活率大 [2]。因此，设计准确可靠的分类器是乳腺肿瘤诊断与治疗中急需解决的关键问题，具有一定的医学价值。传统的乳腺癌诊断检查为细针穿刺细胞学(FNAC)和乳房X光检查 [3] ：FNAC分析取决于病理学、放射学和肿瘤学专家的联合诊断，诊断结果可能因疲劳、经验不足而存在差异，且诊断过程耗时耗力；基于X光技术的诊断存在对X光图像理解因人而异的缺陷。因此，迫切需要开发能够智能、自动化地检测乳腺癌疾病的辅助诊断系统，提高诊断结果的客观科学性。

数据挖掘和机器学习技术为开发旨在减少诊断错误的辅助诊断系统提供了可能。数据挖掘是发现可能无法直接识别的隐藏信息的过程，该技术已成功应用于预测肝脏疾病 [4] [5]，心脏疾病 [6] 以及肺癌 [7]、甲状腺癌 [8] 等疾病。乳腺癌的自动化诊断模型，也已应用了大量的数据挖掘和机器学习技术，例如：概率神经网络、BP神经网络、C4_5算法 [9]、AdaBoost算法。文献 [10] 利用贝叶斯网络、属性选择分类器、J48、逻辑回归模型、One-R建立乳腺癌诊断模型，并用三种不同的特征选择算法对属性进行筛选。文献 [11] 利用Tensorflow深度学习框架搭建了自定义神经网络的乳腺癌模型。文献 [12] 提出了旋转森林的乳腺癌诊断模型，并用遗传算法对数据进行降维。文献 [13] 对AdaBoost算法做出了改进，即增加患病样本被错分为健康样本的权重，并研究了BP神经网络，但忽略了BP网络利用梯度下降算法求解权值，可能陷入局部最优的问题。这些模型的局限性在于它们具有固定的循环，这种固定循环不能提高算法诊断的准确性。

我们在文献 [10] [11] [12] [13] 研究基础上，提出一种混合集成的方法，该混合集成方法用Adaboost [14] 算法做为集成算法。本文分类算法核心思想是对乳腺癌数据集的多种特征用不同的分类算法训练出不同的分类器(弱分类器)，并在处理数据分布权值时，增加患病样本被错分为健康样本的权值，减小健康样本被错分的患病样本的权重；最后通过权重以线性的组合方式将这些弱分类器集成起来，构成最终的强分类器。该混合算法不仅改变了单一算法的固定循环，更考虑了BP网络的局部最优问题。本文仿真数据选取UCI的威斯康星大学乳腺癌数据集，采用多个性能指标进行评估，验证了混合集成医疗诊断模型的有效性与合理性。

2. 混合集成模型

2.1. 样本数据的预处理

乳腺癌数据集样常常伴随变量冗余，无论是从减少计算量提高诊断速度，还是寻找影响疾病的主要因素对样本降维处理是必不可少的工作。样本的降维可描述如下：

给定样本 $\left\{x_{ij}^{\left(0\right)},y_i\left(i=1,\cdots ,p;j=1,\cdots ,q\right)\right\}$，寻找一种映射 $F:R^q\to R^d\left(d\le q\right)$，使映射前后，样本与结果的关联关系保持不变。

常用的降维方法有主成份分析法(PCA principal Component Analysis)、非线性回归法等，对于非线性回归，在样本数据标准化处理后，样本中各元素的绝对值均不大于1，因此非线性回归的显著性检索常常只需要在二阶范围内进行，即：

$y_i\Rightarrow {\displaystyle {\sum }_{j=1}^q{\beta }_{ij}{x}_{ij}}+{\displaystyle {\sum }_{j_1=1}^q{\displaystyle {\sum }_{j_2=1}^q{\gamma }_{i{j}_1{j}_2}{x}_{i{j}_1}{x}_{i{j}_2}}}$。 (1)

PCA方法根据阀值可直接确定出主影响因素，非线性回归则是检测各影响因素的置信度来决定主要影响变量，具体的操作方法见文末实例分析。

2.2. 混合集成原理

设有n种算法，对应第 $k\left(k\le n\right)$ 种算法的弱分类器总数为 $T_k$，则第k种算法的集成分类器为

$H_k={\displaystyle {\sum }_{i=1}^{T_k}{\alpha }_{ki}{g}_{ki}}$， (2)

其中 ${\alpha }_{ki}$ 为第k种算法第i弱分类器 $g_{ki}$ 的集成权重。

对不同算法得到的结果，选择合适的判决策略，得到最后的诊断结果。

$S=f\left(H_1,H_2,\cdots ,H_n\right)$， (3)

这里 $f(•)$ 表判决策略。图1给出了算法的示意图。

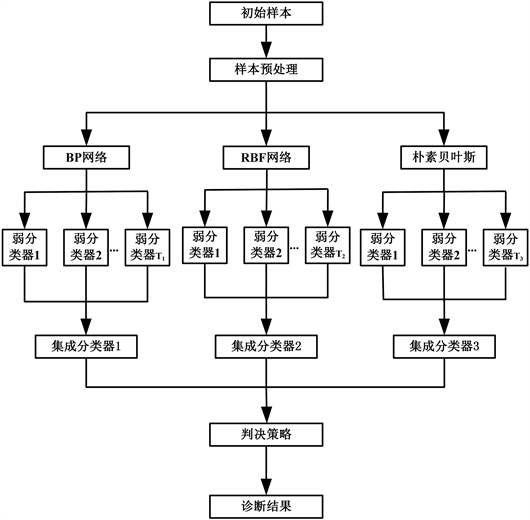
Figure 1. Hybrid ensemble classifier architecture

图1. 混合集成分类

3. 分类器算法

在众多神经网络中BP神经网络应用较为广泛，但由于BP神经网络利用梯度下降算法求解权值，可能陷入局部最优。RBF网络具有全局逼近能力，从根本上解决了BP网络的局部最优问题，因此本文用RBF网络优化BP网络的局部最优问题。本研究数据规模较小，且Naïve Bayes网络对小规模数据分类有良好的性能，在混合模型时加入了Naïve Bayes网络，使得模型分类效果更为良好。因此，本文混合模型的弱分类器算法由BP、RBF、Naïve Bayes三网组成。本研究的混合模型采用AdaBoost算法进行集成，在处理数据权重时选择了误差的指数函数作为权重的修改函数，这是因为指数函数，一使得分类器结果稳定；二是使模型是收敛的；三是使误差率不断减小，以致最后的基分类器误差最小。混合模型算法流程如下：

For k = 1 to n，

For t = 1 to ，

1) 输入数据 $X=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_m,y_m\right)\right\}$，样本的初始分布权值 $D_t\left(i\right)=1/m$。

2) 弱分类器预测。

用训练数据调用算法k，训练T轮后得到 $T_k$ 组弱分类器函数 $h_{T_k}\left(x\right)$，并且得到m组训练样本输出结果 $g\left(i\right)\left(i=1,\cdots ,m\right)$，计算加权误差 $e_t$ ：

$e_t={\displaystyle {\sum }_{i=1}^m{D}_t\left(i\right)\left|g\left(i\right)-y\left(i\right)\right|}$， $i=1,2,3,\cdots ,m$， (4)

式中y_i为样本i的期望分类结果。

3) 根据弱分类器预测误差e_t计算弱分类器权重α_t：

${\alpha }_t=\frac{1}{2}\ln \left(\frac{1-e_t}{e_t}\right)$。 (5)

4) 更新样本的分布权值，调整公式为：

IF (模型输出 ≠ 期望输出) and (期望输出为患病类别)

$D_{\left(t+1\right)}\left(i\right)=k_1{D}_t\left(i\right)\exp \left[-{\alpha }_t{y}_i{g}_t\left(x_i\right)\right]$， $i=1,2,\cdots ,m$， $k_1\ge 1$。 (6)

IF (模型输出 ≠ 期望输出) and (期望输出为健康类别)

$D_{\left(t+1\right)}\left(i\right)=k_2{D}_t\left(i\right)\exp \left[-{\alpha }_t{y}_i{g}_t\left(x_i\right)\right]$， $i=1,2,\cdots ,m$， $0<k_2<1$。 (7)

ELSE $D_{\left(i+1\right)}=D_i$。 (8)

然后对D值进行归一化处理：

$D_{sum}=sum\left(D_{t+1}\left(i\right)\right)$ (9)

$D_{t+1}\left(i\right)=D_{t+1}\left(i\right)/D_{sum}$。 (10)

Next t；

5) 得到由 $T_k$ 组弱分类函数组合得到第k种算法的强分类函数 $H_k\left(x\right)$ ：

$H_k\left(x\right)=sign\left[{\displaystyle {\sum }_{t=1}^T{\alpha }_t{h}_{T_k}\left(x\right)}\right]$ (11)

Next k。

4. 实验及分析

4.1. 数据预处理

本文实验使用乳腺癌威斯康星州诊断(WDBC)数据集作为仿真数据。该数据集来自UCI的机器学习知识库。它包括569名实验对象的32个肿瘤特征。这32个特征由30个实际的肿瘤特征、一个实验对象的ID号和一个表明每个研究对象为良性或恶性肿瘤的类标签组成。如表1所示在这个数据集中，每个细胞核评估10个实值因子。由于医疗数据均比较冗余，导致计算工作量增多，冗余数据的误差传导也影响诊断结果的准确率，需要对数据进行预处理即数据降维。本文采用主成分分析和逐步回归分析对数据进行降维。

Table 1. Dataset properties

表1. 数据集属性

4.1.1. 主分分析

PCA是运用最广泛的线性降维方法之一，主成分分析的实质是：通过正交变换将数据转换为相等数量的线性不相关变量，尽可能保留原始数据特征。PCA算法的主要步骤如下：

1) 输入样本数据 $X=\left\{X_1,X_2,\cdots ,X_n\right\}$ 为n行m列，对数据进行标准化得到矩阵M，

$M=\frac{X_{ij}-{\bar{X}}_j}{\sqrt{var\left(X_j\right)}},i=1,2,\cdots ,n;j=1,2,\cdots ,m$， (12)

其中：

${\bar{X}}_j=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{X}_{ij}}$, $var\left(X_j\right)=\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(X_{ij}-{\bar{X}}_j\right)}^2},j=1,2,\cdots ,m$。 (13)

2) 求矩阵M对应的协方差矩阵：

$M_b=\frac{1}{n-1}{M}^{\text{T}}M$。 (14)

3) 求矩阵M_b的非负的特征根 ${\lambda }_1>{\lambda }_2>\cdots >{\lambda }_P\ge 0$，p为非负特征根的数量， ${\lambda }_i$ 对应的特征向量记为：

$v_i=\left(v_{i1},v_{i2},\cdots ,v_{iP}\right)$, $i=1,2,\cdots ,P$。 (15)

且满足

$v_i{v}_j^{\text{T}}={\displaystyle {\sum }_{k=1}^P{v}_{ik}{v}_{jk}}=\{\begin{array}{cc}1& i=j\\ 0& i\ne j\end{array}$。 (16)

4) 计算累计贡献率即某个特征值占全部特征值合计的比重：

$\eta =\frac{{\displaystyle \sum {\lambda }_i}}{{\displaystyle {\sum }_{i=1}^P{\lambda }_i}}$。 (17)

本文取 $\eta$ 的取值范围为85%~100%，得到贡献率与准确率之间的关系图，如图2所示，准确率随着贡献率大小先升后降，其临届值为95%，此时准确率最高为0.9714。因此本文选取 $\eta$ 为95%，得到贡献率最大的前10个主成分，即21, 22, 23, 24, 25, 26, 27, 28, 29, 30这10个属性。其主成分贡献率直方图如图3所示。

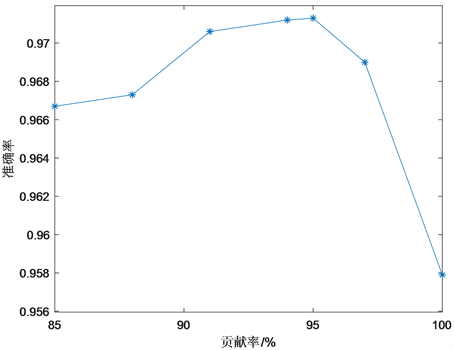
Figure 2. Graph of relation between contribution rate and accuracy rate

图2. 贡献率与准确率关系图

Figure 3. Contribution rate histogram

图3. 贡献率直方图

4.1.2. 逐步回归分析

逐步回归分析通过逐个引入变量进行F检验(检测过程参见文献 [13] )，保证最后所得的变量均为显著的。经过逐步回归后得到6, 8, 11, 14, 15, 17, 21, 22, 24, 27, 28, 29, 30的13个属性。

4.2. 评价指标

为检验模型有效性，本研究以准确率、误差、漏诊率、灵敏度、特异度和Youden指数作为分类评价指标。假设样本总数为sum，TP是将恶性肿瘤诊断为恶性肿瘤数量，FN是将恶性肿瘤诊断为良性数量， FP是将良性诊断为恶性肿瘤数，TN是将良性类诊断为良性数。

a) 准确性：相对于测试的样本总数sum，正确分类为给定类别的肿瘤的百分比，公式为：

$\text{Accury}=\frac{\text{TP}+\text{TN}}{\text{sum}}$。 (18)

b) 漏诊率MDR (Missed diagnosis rate)：漏诊率是实际为恶性肿瘤的样本中，预测为良性的占比，公式为：

$\text{MDR}=\frac{\text{TP}}{\text{TP}+\text{FP}}$。 (19)

c) 灵敏度Sen (Sensitivity)：研究对象诊断为恶性肿瘤的概率，公式为：

$\text{Sen}=\frac{\text{TP}}{\text{TP}+\text{FN}}$。 (20)

d) 特异度Spe (Specificity)：实际上良性被诊断为良性的概率，公式为：

$Sen=\frac{TP}{TP+FN}$。 (21)

e) 约登指数：是评价筛查试验真实性的方法，公式为：

$Youden=\frac{TP}{TP+FN}+\frac{TN}{TN+FP}-1$。 (22)

f) 误差率：相对于测试的总样本数sum，错误分类为给定类别的肿瘤的百分比，公式为：

$Error=\frac{FP+FN}{sum}$。 (23)

为了研究主成分分析和逐步回归分析对准确率的影响，表2列出了10折交叉验证100次两种模型的准确率，误差率，漏诊率，灵敏度，特异度和约登指数，可见在约登指数上，逐步回归归分析相对于主成分分析提高了0.007，在漏诊率上，逐步回归归分析相对于主成分分析降低了了0.196，其原因可能是主成分分析降维为10个属性，丢失的信息较多，且其降维后得到的属性也有差距，每个属性代表的信息不同，因此主成分分析的约登指数略低，漏诊率略高。因此本文选用逐步回归方法对数据进行预处理。

Table 2. Stepwise regression and principal component analysis

表2. 逐步回归与主成分分析

4.3. 混合集成与单一算法比较

为了验证提出的混合集成模型的有效性，将混合集成模型与单一算法统一采用逐步回归对数据进行约简，并将其准确率，误差率，漏诊率，灵敏度，特异度和约登指数做比较。各指标10折交叉验证100次的平均值如图4所示。

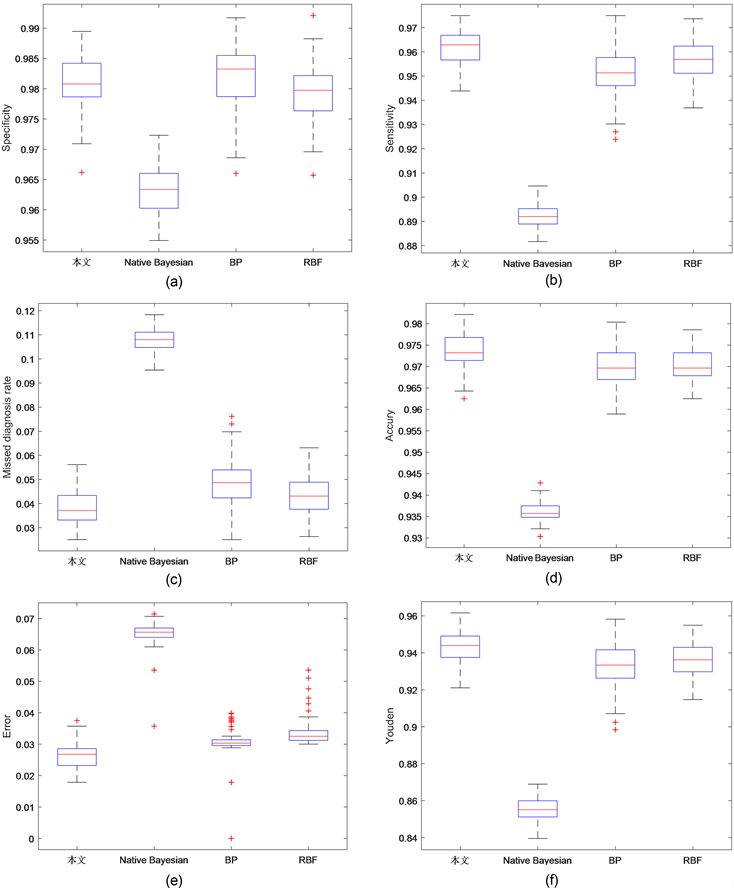
Figure 4. Contribution rate histogram. (a) Specificity box diagram of the four models; (b) Sensitivity box diagram of the four models; (c) Boxes of missed diagnosis rates of the four models; (d) Boxes of accuracy of the four models; (e) Error box diagram of the four models; (f) Youden index box diagram of the four models

图4. 贡献率直方图。(a) 四种模型的特异度盒图；(b) 四种模型的灵敏度盒图；(c) 四种模型的漏诊率盒图；(d) 四种模型的准确率盒图；(e) 四种模型的误差盒图；(f) 四种模型的Youden指数盒图

如图4(a)和图4(b)所示，BP、RBF和本文的混合模型都具有较高的特异度和灵敏度，这表明三种网络能更好的逼近函数，使模型的特异度和灵敏度较高。在灵敏度上本文的混合模型均值为0.962，BP均值为0.951，RBF均值为0.958，Naïve Bayes均值为0.892，可见本文的混合模型均优于其他三种模型，说明本文的算法能更好的检测出患病的样本。在特异度上本文的混合模型均值为0.981略低于BP网络0.983，可能是由于本文降低了健康样本被错分为患病样本的权重，以致降低了检测出健康样本的概率。

如图4(c)和图4(d)所示，在准确率上本文的混合模型均值为0.973，BP均值为0.970，RBF均值为0.970，Naïve Bayes均值为0.935。在漏诊率上本文的混合模型均值为0.037；BP模型的均值为0.048；RBF模型的均值为0.043；Naïve Bayes模型的均值为0.107；可见在准确率和漏诊率上本文的混合模型都优于单一的算法，说明本文的混合模型提高了单一算法的准确率，且能更容易的检测出患病样本。

如图4(e)和图4(f)所示，在误差率上本文的混合模型均值为0.027，BP均值为0.030，RBF均值为0.032，Naïve Bayes均值为0.065；在Youden指数上本文的混合模型上均值为0.944，BP均值为0.933，RBF均值为0.936，Naïve Bayes均值为0.855；由此说明本文的混合模型增强了模型的真实性，提高了综合诊断能力。

综上所述BP、RBF和本文的混合模型由于可以任意精度的逼近任何非线性函数，各指标均比Naïve Bayes高。本文的混合模型在准确率、误差、漏诊率、灵敏度和Youden指数方面都优于这些单一算法，但在特异度上略低于BP网络，可能是本文降低了健康样本被错分为患病样本的权重，以致降低了检测出健康样本的概率。

5. 结论

本文提出了一种新的混合集成方法，且该方法在处理数据权重时，加重了被错分的患病样本的权重，减小被错分的健康样本的权重，以此来改进乳腺癌早期诊断的分类算法。研究结果表明，使用混合集成技术将提高单一算法检测乳腺癌的性能。

本研究提出的算法在准确率上还有待提高，未来我们将以各种集成技术和分类算法扩展提出新的方法，以提高分类的准确率。

致谢

本篇论文从选题，润色以及最后的投稿我的导师张志飞教授都给了我很多的指导和建议，这篇文章才得以圆满完成。在学习生涯中，能遇到张老师，是我一生的幸运。张志飞教授和蔼可亲，科学态度严谨。在生活上给予我无微不至的关怀，在学术上也以严谨的态度要求我，给予我富有前瞻性和启发性的指导，跟着张老师使我在分析和独立解决问题能力等方面都得到了提高，尤其是在以后的人生方向更使我目标明确。在此，我要向张老师表达衷心的感谢。同时还要感谢师姐刘士亚，小组成员张君以及立胜公司的陈旭给予我的宝贵建议。祝愿他们身体健康。