1. 引言
M通道多速率滤波器组(如图1所示)在图像压缩、数字通信、雷达等很多领域都有广泛的应用 [1]。它首先用分析滤波器组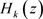 将全带的输入信号分解成一系列不同频带的子带信号。由于带宽降低了,因而可以进行下采样。根据特定应用,可以对这些子带信号进行适当处理。若不改变这些子带信号可以上采样,并用综合滤波器组
将全带的输入信号分解成一系列不同频带的子带信号。由于带宽降低了,因而可以进行下采样。根据特定应用,可以对这些子带信号进行适当处理。若不改变这些子带信号可以上采样,并用综合滤波器组 重构为原信号(有延迟)。在该系统中,共有2M个滤波器需要设计。当通道数M较大时,很难设计数量众多的滤波器。伪正交镜像滤波器组 [1] - [10] 是一种特殊的滤波器组,它的分析滤波器组
重构为原信号(有延迟)。在该系统中,共有2M个滤波器需要设计。当通道数M较大时,很难设计数量众多的滤波器。伪正交镜像滤波器组 [1] - [10] 是一种特殊的滤波器组,它的分析滤波器组 和综合滤波器组
和综合滤波器组 是通过对一个原型低通滤波器进行调制得到的。其好处是:(1) 整个滤波器组的设计可以简化为一个原型滤波器的设计,大大降低了设计的复杂度和难度。(2) 滤波器组可以通过余弦变换快速实现。
是通过对一个原型低通滤波器进行调制得到的。其好处是:(1) 整个滤波器组的设计可以简化为一个原型滤波器的设计,大大降低了设计的复杂度和难度。(2) 滤波器组可以通过余弦变换快速实现。

Figure 1. M-channel multirate filter bank
图1. M通道多速率滤波器组
Koilpillai和Vaidyanathan建立了伪正交镜像滤波器组的精确重构条件,给出了满足精确重构条件的格型结构 [2]。通过优化格型系数可以在结构上保证滤波器组的精确重构性。但目标函数(例如滤波器的阻带衰减)往往是格型系数的高度非线性函数,阻带衰减对格型系数的变化非常敏感,很难获得具有高阻带衰减的滤波器组 [3]。然而在有些应用中,如高保真音频信号编码中,需要约−100 dB的阻带衰减 [5] [11]。为了获得高阻带衰减的滤波器组,放松精确重构性,即采用近似重构的滤波器组是一个明智的方法。Nguyen采用有约束的最小二乘法设计了具有高阻带衰减的滤波器组 [3]。但该方法使用了非常多的优化变量,优化方法非常复杂。Doblinger提出了一个快速设计算法,在该方法中需要迭代求解带线性约束的二次规划问题并且仍然需要大量的优化变量 [4]。Creusere和Mitra提出了一个高效的单参数优化方法 [5]。该方法通过调整原型滤波器的通带边缘频率,用Parks-McClellan算法迭代设计原型滤波器。但Parks-McClellan算法计算量较大且无法兼容时域和频域约束。本文则将原型滤波器表示为特征滤波器 [12],通过改变原型滤波器的通带边缘频率对滤波器组进行单参数优化设计。在该方法中,原型滤波器的系数向量是通过求解一个实对称矩阵的最小特征值对应的特征向量得到的,不需要求出其它特征向量,因而可以用高效的算法计算。此外,文献 [5] 的目标函数是在频域离散化获得的,而本文的目标函数根据Nyquist性质在时域做2M倍抽取获得的,因而计算更加简单。
2. 滤波器组设计
在伪正交镜像滤波器组中,原型滤波器 是一个低通线性相位滤波器,假定其脉冲相应
是一个低通线性相位滤波器,假定其脉冲相应 的长度为N。分析滤波器组的脉冲响应
的长度为N。分析滤波器组的脉冲响应 和综合滤波器组的脉冲响应
和综合滤波器组的脉冲响应 可以通过原型滤波器的余弦调制获得:
可以通过原型滤波器的余弦调制获得:
 (1)
(1)
 (2)
(2)
其中 ,
,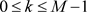 。因而伪正交镜像滤波器组的设计可以归结为原型滤波器
。因而伪正交镜像滤波器组的设计可以归结为原型滤波器 的设计。
的设计。
要使伪正交镜像滤波器组具有近似重构性,原型滤波器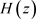 应满足如下条件 [5]
应满足如下条件 [5]
 ,
, (3)
(3)
 ,
, (4)
(4)
整个伪正交镜像滤波器组具有线性相位响应,重构信号没有相位失真,因而只需要考虑幅度失真和混叠失真。满足条件(4)可以消除幅度失真。混叠失真来自于相邻子带和非相邻子带。相邻子带产生的混叠是混叠的主要部分,可在余弦调制中通过选择合适的相位因子加以消除。高阻带衰减可以近似满足条件(3),从而大大抑制非相邻子带产生的混叠。
传统上,设计原型滤波器的方法有最小二乘法,Parks-McClellan算法等方法。最小二乘法需要矩阵求逆运算,因而计算量大,并且对高阶滤波器的设计存在数值问题。Parks-McClellan算法无法兼容时域约束和频域约束。本文则将原型滤波器表示为特征滤波器,原型滤波器的系数向量是通过求解一个实对称矩阵的最小特征值对应的特征向量得到的,不需要求出其它特征向量,因而可以用高效的算法计算。
为简单起见,假定原型滤波器的长度N是偶数。原型滤波器具有线性相位,其脉冲相应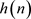 是对称的,即
是对称的,即
 (5)
(5)
因此,只有一半的原型滤波器系数需要求解。原型滤波器的频率响应 可以写为:
可以写为:
 (6)
(6)
其中 是
是 的幅度响应,具有如下形式:
的幅度响应,具有如下形式:
 (7)
(7)
其中
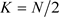 (8)
(8)
 (9)
(9)
定义
 (10)
(10)
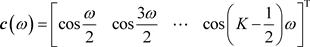 (11)
(11)
则有
 (12)
(12)
对于一个典型的低通滤波器,其典型的期望响应 具有如下形式
具有如下形式
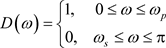 (13)
(13)
其中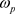 和
和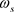 分别是滤波器的通带和阻带边缘频率。
分别是滤波器的通带和阻带边缘频率。
为了逼近期望响应 ,需要极小化滤波器的阻带误差能量
,需要极小化滤波器的阻带误差能量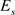 和通带误差能量
和通带误差能量 。
。
 (14)
(14)
其中 是一个实对称正定矩阵
是一个实对称正定矩阵
 (15)
(15)
显然原型滤波器阻带误差能量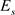 是原型滤波器系数
是原型滤波器系数 的二次函数。然而,原型滤波器的通带误差能量
的二次函数。然而,原型滤波器的通带误差能量 却不是原型滤波器系数
却不是原型滤波器系数 的二次函数
的二次函数
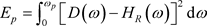 (16)
(16)
为了将通带误差能量 表示为原型滤波器系数
表示为原型滤波器系数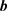 的二次函数,令通带的期望响应
的二次函数,令通带的期望响应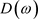 是通带幅度响应的均值:
是通带幅度响应的均值:
 (17)
(17)
 (18)
(18)
其中 是通带内P个均匀划分的离散频率点。用
是通带内P个均匀划分的离散频率点。用 代替(16)中的
代替(16)中的 ,可以得到
,可以得到
 (19)
(19)
其中 是一个实对称正定矩阵
是一个实对称正定矩阵
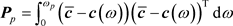 (20)
(20)
定义总的误差能量E为阻带误差能量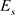 和通带误差能量
和通带误差能量 的凸组合:
的凸组合:
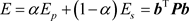 (21)
(21)
其中 是控制通带和阻带相对权重的权系数,
是控制通带和阻带相对权重的权系数, 。
。
显然 是上述优化问题的平凡解。为了避免该平凡解,对解进行单位范数约束
是上述优化问题的平凡解。为了避免该平凡解,对解进行单位范数约束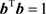 。根据瑞利原理,总的误差能量E的最小值是矩阵
。根据瑞利原理,总的误差能量E的最小值是矩阵 的最小特征值。最优解
的最小特征值。最优解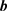 就是该最小特征值所对应的特征向量。由于只需要求解一个特征向量(而不是全部特征向量),因此可以使用迭代法进行快速计算 [1]。
就是该最小特征值所对应的特征向量。由于只需要求解一个特征向量(而不是全部特征向量),因此可以使用迭代法进行快速计算 [1]。
经典的滤波器组优化设计需要优化设计原型滤波器的系数。当滤波器长度很长时,需要优化大量的滤波器系数,因而计算量很大且难以获得高的阻带衰减。下面我们仅优化原型滤波器的通带边缘频率 。
。
显然,一个有限长度的原型滤波器无法精确满足条件(3)和(4)。条件(3)可以通过高阻带衰减近似满足。条件(4)可以作为目标函数进行极小化。然而该目标函数需要在频域用一系列密集的网格进行离散化处理和计算,因而计算量大且不准确。
满足精确重构条件的原型滤波器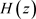 是Nyquist (2M)滤波器
是Nyquist (2M)滤波器 的谱因子。
的谱因子。
 (22)
(22)
因此滤波器 的脉冲响应
的脉冲响应 满足
满足
 (23)
(23)
所以我们极小化下列目标函数
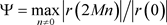 (24)
(24)
其中
 (25)
(25)
由于不需要计算全部的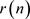 ,只需要计算
,只需要计算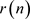 的2M抽取,即只需要计算很小一部分的
的2M抽取,即只需要计算很小一部分的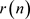 ,因而计算量大大降低。
,因而计算量大大降低。
整个滤波器组的优化设计过程归纳如下:
1) 选择滤波器组的通道数 M 和滤波器长度N。设定原型滤波器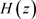 的通带边缘频率
的通带边缘频率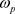 ,阻带边缘频率
,阻带边缘频率 通常设定为
通常设定为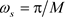 。
。
2) 选择通带边缘频率 的步长参数b和搜索方向a (a = 1 or −1)。令初始的目标函数是一个较大的数,例如104。
的步长参数b和搜索方向a (a = 1 or −1)。令初始的目标函数是一个较大的数,例如104。
3) 计算 。
。
4) 用上述特征滤波器法设计原型滤波器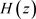 。
。
5) 根据式(24)计算目标函数。
6) 如果相邻两次迭代中目标函数变化小于一个预先指定的值,则优化停止,否则转向下一步。
7) 如果本次迭代的目标函数小于上次迭代的目标函数,转向3),否则令b = b/2, a = −a转向3)。
在每次迭代过程中都需要设计一次原型滤波器,因此采用了高效的特征滤波器法和单参数优化方法可以大大降低整个滤波器组的设计复杂度。
3. 设计举例
根据上述优化设计方法,设计了一个5通道伪正交镜像滤波器组。图2给出了原型滤波器的幅度响应。图3给出了分析滤波器组的幅度响应。可见,滤波器组具有很高的阻带衰减,阻带衰减约为−100 dB。
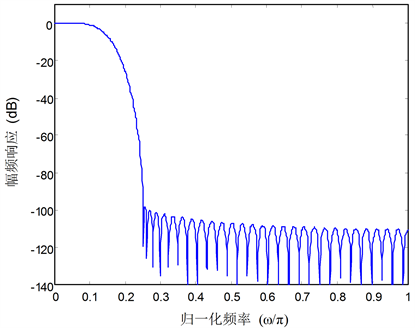
Figure 2. Amplitude response of the prototype filter
图2. 原型滤波器的幅频响应

Figure 3. Amplitude responses of the analysis filters
图3. 分析滤波器组的幅频响应
4. 结论
伪正交镜像滤波器组的设计通常需要优化大量的参数,本文提出了一个基于特征滤波器法的单参数优化设计方法。在该方法中,仅仅需要调整原型滤波器的通带边缘频率就可得到高阻带衰减的滤波器组。原型滤波器的系数向量是通过求解一个实对称矩阵的最小特征值对应的特征向量得到的。由于无需求解全部的特征向量,因而具有较高的计算效率。此外,根据Nyquist滤波器的性质,本文在滤波器组的优化设计中还提出了一种基于抽取的时域目标函数,避免了传统方法需要频域离散化的缺点,进一步降低了计算量,特别适合于设计高复杂度的滤波器组。