1. 引言
秘密共享是当今生活中广泛使用的技术,主要是对信息进行加密和保护,防止外泄。自Shamir和Blakley [1] [2] 引出秘密共享的问题并给出了非常简单的问题解决方案以来,关于这一主题的研究已经深入。Shamir和Blakley的方案是在没有故障的模型中有效的解决方案。Tompa和Woll [3] 以及McEliece和Sarwate [4] 的方案在存在故障的模型中给出了部分解决方案。近年来,许多学者已经开始研究秘密共享技术,并提出了各种秘密共享方案,其中有中国剩余定理、双线性对技术、签密与消息恢复算法、公钥密码体制等。蒋华等人基于公钥密码体制,对其进行改进,提出了一种双向认证的方案。只要是在申请人,身份验证者和服务器之间的相互身份验证加密 [5]。2014年张柄虹等人提出了一种方案,在该方案中,秘密分发的过程是独立的,并且与参与者的私钥计算分开 [6]。2018年,谷婷提出了一种秘密共享方案 [7]。在该方案中,秘密份额由参与者产生,利用签密与消息恢复算法,参与的所有人都可以查验分发者的份额。
在秘密共享方案飞速发展的下,对于方案的正确性、有效性和安全性变得重要起来,即秘密共享方案的可验证有着十分深远的研究意义。Chor等人 [8] 第一次定义了可验证秘密共享的完整概念,并给出了问题的解决方案。接下来的研究,在各种不同假设下,不同的学者给出了问题的解决方案。只是为了实现可验证性的目标,这些协议偏离了原始解决方案的简单性。它们需要繁重的计算和广泛的零知识证明。此外,为了重建秘密,还需要进行大量计算。大量的研究和实际操作表明,简单的协议是很重要的。Gennaro的方案基于Shamir的秘密共享方案,并增加了额外的低成本结构。这种结构基本上是参与者对持有秘密的公开承诺。
2. 基本知识
本文设计的可验证性秘密共享方案涉及到以下三个知识:① shamir门限秘密共享方案;② 零知识证明 [9] ;③ Pedersen承诺协议 [10]。
Shamir的门限秘密共享方案通过构造多项式,利用多项式进行秘密的分享,本文秘密共享是基于Shamir门限秘密共享方案实现的;本文使用的零知识证明改编自Cramer和Damgar的方案,使其更具有证明的一般性,是本文计算阶段中的重要一环;Pedersen承诺协议是一个满足无条件秘密性的同态承诺协议,作为本文可验证性设计的基本框架。
3. 秘密共享方案及可验证性设计设计
3.1. 秘密共享方案
本文将Gennaro的VSS方案和Pedersen同态承诺方案结合,实现了对份额正确性的验证。该MPC协议将待计算函数表示为加法和乘法组成的有向图,通过进行对应的加法协议和乘法协议来实现计算,其结构如图1所示。该协议可分为初试化阶段,输入阶段,计算阶段和输出阶段。

Figure 1. Structure of the secret sharing scheme
图1. 秘密共享方案结构
初始化阶段:假设协议有n个参与者,分别记作
,每个参与者分别对应一个公开身份数
,以及一个秘密
。n个参与者协商一个大素数p,该素数满足
,其中q也是素数,g为
的q阶元,h为g生成的子群中的随机元素。上述的
是构造可验证性使用的承诺函数的参数。
输入阶段:每个参与者
独立随机地选择
个t次多项式,使用上述多项式分别在有理数域上共享
,即
(3-1)
其中
为参与者
的秘密。
同样的,
生成随机数
,并独立地随机选择两个t次多项式
,分别在有理数域上分享
,即
。 (3-2)
分别使用式(3-1) (3-2)计算
,并将
发送给
,其中
。同时,
将承诺集合
,进行广播,
。 (3-3)
计算阶段:步骤(1):n个参与者约定在式(3-2)中的
取定
个随机多项式,不妨就将这
个多项式记为
,其对应的
参与者分别是
。每个参与者
计算
(3-4)
承诺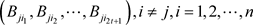 进行广播。
进行广播。
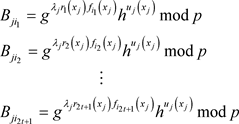 (3-5)
(3-5)
其中 为
为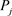 随机选择与承诺相关的t次多项式。
随机选择与承诺相关的t次多项式。
步骤(2):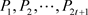 中的每个
中的每个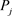 随机选择n个t次多项式
随机选择n个t次多项式 分别用来共享
分别用来共享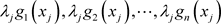 ,其中
,其中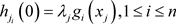 ,接着随机选择1个t次多项式
,接着随机选择1个t次多项式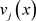 用来共享
用来共享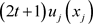 ,即
,即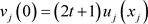 。然后
。然后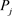 计算
计算 ,并将
,并将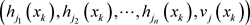 发送给
发送给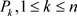 。承诺集合
。承诺集合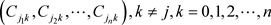 。其中,当
。其中,当 时,有
时,有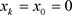 。将承诺集合进行广播,
。将承诺集合进行广播,
 。 (3-6)
。 (3-6)
输出阶段:对于每个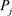 ,计算输出
,计算输出
 (3-7)
(3-7)
其中,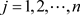 ,广播承诺集合
,广播承诺集合
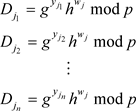 (3-8)
(3-8)
其中, 。
。
重构阶段:每个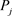 具有输出
具有输出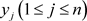 。使用拉格朗日插值公式,任意的
。使用拉格朗日插值公式,任意的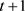 个参与者都可以恢复
个参与者都可以恢复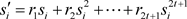 。
。
3.2. 可验证性分析
3.2.1. 输入阶段的可验证性
以 为例,根据式(3-3)所示,有承诺
为例,根据式(3-3)所示,有承诺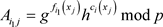 ,则根据(3-1)式,可将多项式组写成矩阵乘积的形式
,则根据(3-1)式,可将多项式组写成矩阵乘积的形式

不妨记为:
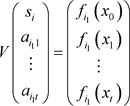
根据上述多项式,容易得到矩阵V是可逆的,所以可将上式写成:
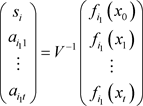
对于任意的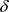 ,有
,有
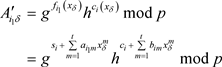
为了方便起见,记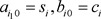 ,则上式记作
,则上式记作
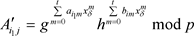 (3-9)
(3-9)
记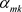 为
为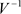 的第m行第k列的值,所以可得
的第m行第k列的值,所以可得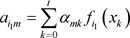 ,并代入到式(3-9)中,可得
,并代入到式(3-9)中,可得
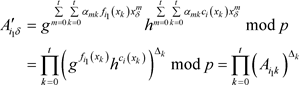
其中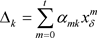 ,以上所述,将
,以上所述,将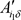 与
与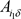 作比较,即可验证自己收到的份额是否和其他参与者收到
作比较,即可验证自己收到的份额是否和其他参与者收到
份额出自同一组多项式(这里不妨记作VSPS性质),从而来判断自己收到的份额是否有效,即正确性得到检验。
3.2.2. 计算阶段的可验证性
第一步:经过了输入阶段的验证,每个参与方 已经收到经过输入阶段VSPS验证的正确份额
已经收到经过输入阶段VSPS验证的正确份额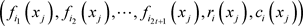 ,以此承诺函数
,以此承诺函数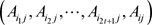 也是经过VSPS验证被证实正确的。利用正确承诺函数
也是经过VSPS验证被证实正确的。利用正确承诺函数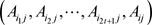 和
和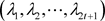 并使用前文提到的零知识证明方法,每一个参与者
并使用前文提到的零知识证明方法,每一个参与者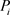 对
对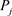 广播的承诺
广播的承诺 进行比较,来保证正确的秘密份额被使用。
进行比较,来保证正确的秘密份额被使用。
第二步:根据上述第一步,参与者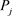 有经过前面检验的
有经过前面检验的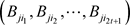 ,根据式(3-6),可验证性如下:
,根据式(3-6),可验证性如下:
以 为例,
为例,
1) 当 时,即
时,即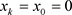 时,即:
时,即:
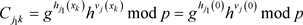
所以有 ,根据
,根据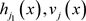 的定义,原式可以写成:
的定义,原式可以写成:
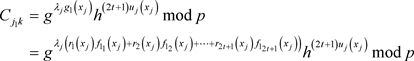
所以,根据模的运算性质,和承诺函数集合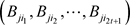 的形式,上式可以写成
的形式,上式可以写成
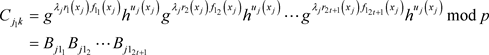
所以,在步骤(1)中,验证正确的承诺函数集合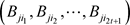 ,就可以将
,就可以将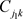 与
与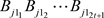 的乘积作比较,可以判断函数
的乘积作比较,可以判断函数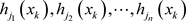 是否分别用来共享
是否分别用来共享 。
。
2) 当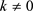 时,同理如输入阶段,使用VSPS验证来验证自己收到的份额是否有效。
时,同理如输入阶段,使用VSPS验证来验证自己收到的份额是否有效。
3.2.3. 输出阶段的可验证性
经过了计算阶段的验证,每个参与方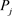 已经收到了经过验证的正确的份额
已经收到了经过验证的正确的份额
 ,和验证正确的承诺
,和验证正确的承诺
根据式(4-7),并以式(4-8)中的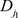 为例,
为例,

将参与者 的承诺
的承诺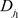 与计算阶段经过验证的承诺
与计算阶段经过验证的承诺 作比较,就可以判断对于输出的
作比较,就可以判断对于输出的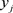 是否是正确的。
是否是正确的。
4. 结束语
关于安全多方计算协议的构造一直是密码学领域中的一个难解的问题。本文针对个Shamir门限的组合的秘密共享方案的可验证性进行设计,完成了Shamir门限组合的秘密共享方案的通用可验证性。该项研究有着很重要的意义。现实中攻击者都是理性的,已有很多学者 [11] 采取惩罚措施,约束恶意攻击者来实现安全多方计算中最难实现的公平性。这些利用惩戒措施实现公平性的研究,都是建立在可验证秘密共享方案的基础上,只有尽可能完全的实现可验证性,对不诚实的恶意参与者进行有效的识别,才能使惩戒措施有效的发挥作用。其次,本文的方案追求的是尽可能完整的可验证性,所以在计算上会有些复杂,这也为下一步的研究指明了方向。
基金项目
国家自然科学基金(No.U1603116、No.61672509)。