基于多元统计的儿童票定价策略的更新研究

A Study on Updating Children Ticket Pricing Strategies Based on Multivariate Statistics

摘要: 现如今，随着人民生活条件日益提升，更多的家庭会选择出游来度过闲暇时光，也正因此，旅游景点、公园等的门票定价问题逐渐为大家热议；而其中，儿童门票也因为当下儿童身高普遍较以往身高而言更高而饱受争议。是否符合购买儿童门票的标准是其中关键问题所在。以往以固定1.2米作为身高标准的方式，在如今各地区生活水平发展不同、地域因素、儿童营养摄入水平不同等条件下，不再是一个最适合的作为衡量的标准。因而，本文试图通过轮廓分析法，针对收集的来自2000年到2015年的几个年份间全国、上海、江西、四川各地区3到10岁儿童平均身高数据，检验不同地区、不同时代等儿童身高轮廓是否相似，从而判断是否有必要分地区制定不同身高标准；检验不同时代儿童身高轮廓是否重合，从而判断是否有必要在现今制定新的身高标准。使用MATLAB软件分析数据得到结果，结果表明各个地区身高轮廓完全相似，因而可以从全国范围制定统一标准；各时代身高有显著差异，因而有必要在当代更新儿童门票身高标准。

Abstract: Nowadays, with the increasing living conditions of the people, more families will choose to travel to spend their leisure time. Therefore, the ticket pricing issues of tourist attractions, parks, etc. are gradually being discussed for everyone; The current height of children is generally higher than in the past and is controversial. The criteria for meeting the purchase of children’s tickets are key issues. In the past, the method of fixing 1.2 meters as the standard of height is no longer the most suitable standard for measurement under the conditions of different living standards, geographical factors and different levels of nutritional intake of children in various regions. Therefore, this paper attempts to test the height of children from different regions and different ages by using the profilometry method to collect the average height data of children aged 3 to 10 in the national, Shanghai, Jiangxi and Sichuan regions from 2000 to 2015. Whether the contours are similar, to determine whether it is necessary to set different height standards by region; to check whether the contours of children’s heights coincide in different eras, and to judge whether it is necessary to set new height standards today. Using MATLAB software to analyze the data and obtain the results, the results show that the height contours of each region are completely similar, so it is possible to develop uniform standards from all over the country; there are significant differences in heights in each era, so it is necessary to update the height standards of children's tickets in the contemporary era.

1. 引言

1.1. 课题缘起

随着时代的发展，现实的资源与条件变得越来越好，人们的生活质量都有所提高。同时，伴随着社会的进步，每个家庭承担的经济压力也在逐渐减少。面对这样条件充裕的生活，人们开始把焦点从追求物质财富转向追求精神财富。家长们更是希望通过旅游等娱乐方式陪伴孩子，并通过此来增长他们对各地风情习俗的认识了解，丰富他们童年的记忆。在游玩过程中，自然是少不了各种门票的购买，其中，各种儿童票便成为了大家的关注热点。

从1997年开始，国家政府为了保障儿童权益，通过以儿童身高为标准，在各种门票中开始实施对部分儿童票价减免的政策，其中在国家颁布的《铁路旅客运输规程》中将儿童票购票、补票的身高限制为1.1米至1.4米。然而，随着经济的快速发展、生活水平的提高、营养状况和成长环境的改善，孩子们的身高与以前同等年龄的孩子相比起来，都有着非常明显的变化，大多数的儿童身高超过了儿童票的标准，让以前制定的身高限制变得有些陈旧。尽管在2010年铁道部已将儿童票的身高标准从之前的1.1米至1.4米，调整到现在的1.2米至1.5米，即身高上下限均增加10厘米，但仍然无法解决儿童与成人的划分标准 [1] (王琨，2019)。同时除了铁道上的儿童票标准，其他景区游乐场的标准也是亟待改革的。

2018年1月份，曾有一位爸爸带着10岁女儿到上海迪士尼游玩，女儿因高达1米4被要求购买成人票，最终这让法官爸爸起诉了迪士尼 [2]。这件事把儿童票问题带到了人们眼前，引起了热议，不少学者对儿童票的标准问题进行了研究，提出了他们的意见。儿童票的施行是本着对儿童权益保护的宗旨，却让部分儿童的权益受到损害。这样实际生活中的一件事，说明了儿童票收费标准亟待更新。

面对多方面因素引起的儿童平均身高的增加，以及目前儿童票的收取标准存在的诸多问题，合理地更新对儿童票价的衡量标准，制定出更加具体可行的儿童票定价依据，便是维护儿童在此方面权益的关键。

1.2. 研究现状

目前有着不少的学者在儿童身高及影响因素与儿童票收取标准上进行学术研究。2018年4月，中国青年报社社会调查中心联合问卷网，对1969名儿童家长进行的一项调查显示，56.7%的受访家长认为以身高作为儿童票收取标准不合理，67.1%的受访家长赞同儿童票收取以年龄为准 [3] (潘铎印，2018)。从这些百分比数据中，可以看出目前儿童票收取标准亟待更新。

2005年中国青少年成年身高已赶上日本；城市中，7岁男、女孩童身高(反映早期发育)的平均值，以及全学龄段身高的平均值已赶上日本，但因乡村群体的相对滞后，整体上仍低于日本，而我国各群体体格发育潜力都很大 [4] (季成叶，张欣，尹小俭等，2011)。学者王坤也曾指出：根据我国疾控部门统计的数据显示，早在2012年全国6岁城市男童平均身高已达到1.2米，12岁未成年人平均身高已超过1.5米 [1]。本次项目需要在这些对儿童身高变化研究的基础上，联合儿童票的制定进一步对儿童票标准加以改善。

儿童票从“量身高”转为“看年龄”，符合儿童成长规律，也是对儿童法定福利政策的维护，体现了为民办实事的态度 [5] (江德斌，2019)。冯海宁(2018)依照实际情况也提出儿童免票要兼顾身高和年龄“双标准”，扩大儿童免票范围，保障儿童福利，让免票政策走向合理化 [6]。还有其他学者都对儿童票收取标准提出了笼统的“看年龄”、“双标准”意见，但其中缺少实际数据的支持和对标准的具体更新内容。

目前国内对儿童身高生长状况，遗传潜能发展状况的调查研究方法相对成熟，大致有多阶段分层整群抽样，体格测量和问卷进行调查等 [7] (王姿欢，蒋竞雄，杨琦等，2016)。再加上多种多元统计方式，能对收集到的数据有很好的处理和运用。

同时，史洪举(2019)也曾在其论文中提及：理当用发展的眼光看问题，妥善平衡各方利益，出台更加有利于保障儿童权益的儿童票标准 [8]。就迪士尼事件，徐建辉(2018)认为：不看身高看年龄，才更凸显儿童优惠政策的普惠性和公平性 [9]。

1.3. 研究原因

前人有的对儿童身高的变化进行了研究，也有学者如丁家发(2019)提出“身高兼顾年龄”的儿童票标准的意见，他认为只有如此，才能彻底终结儿童票标准之争，让儿童票真正回归其应有之义 [10]。这些都说明了目前儿童票的标准已经变得陈旧，不再适用。但这一问题的提出均是来自于平时生活中的实际情况与我们主观认为。在这样的情况下，我们需要通过对实际数据的收集，加以理论知识的证明和分析，用具体的结果来更有力地说明现在的标准确实存在不足之处，儿童门票的收取需要制定一个更好的标准。

2. 数据描述

通过国民体质监测公报和统计年鉴等相关文献，收集到从2000年到2015年的几个年份间，全国、上海、江西、四川各地区3到10岁儿童平均身高的二手数据，共172条。其中全国3~10岁儿童平均身高的数据是由国家体育总局、教育部、国家统计局等10个部门，从全国31个省(市、区)的近3000个机关单位中收集、计算所得。通过以全国儿童身高的数据为基础，分析沿海发达城市(以上海、江西为例)以及内陆省份(以四川为例)的相关数据，从而说明不同地区的儿童身高轮廓是相似的。

收集到数据之后，对数据进行整理和初步描述性统计分析，以待后续详细处理。通过MATLAB代码编程，按照年份、城市和性别的不同，把收集到的数据分成了不同的数据集，并将各组中儿童的年龄与身高相对应，例如：2005年，上海3到10岁的女孩平均身高分别为：100.6 cm，106.7 cm，113.4 cm，118.7 cm，125.9 cm，131.6 cm，137.4 cm，143.5 cm [11] ；2010年对于全国来说，3到10岁的男孩平均身高分别为：101.2 cm，107.1 cm，113.7 cm，118.6 cm，125.5 cm，130.7 cm，135.8 cm，140.9 cm [12]。并做出各组图形，其中部分如图1所示。

Figure 1. 2010 national 3 - 10 year old male and female children height line chart

图1. 2010年全国3~10岁男女儿童身高折线图

从图1可以看出：2010年的3~10岁的儿童的身高大致在100 cm至140 cm之间。因为收集到的数据均是各年龄段的平均身高，从而可知部分10岁孩童的身高在140 cm以上，甚至可能在150 cm左右。

从图2、图3对比可以看出：同一年，城镇儿童的平均身高要高于农村同龄儿童的平均身高。出现此种现象可能是由于家庭经济水平、生活环境以及儿童所受到的营养程度等多方面因素造成的。

Figure 2. Broken line of height of children aged 3 - 10 in cities and towns in China in 2015

图2. 2015年全国城镇3~10岁男女儿童身高折线图

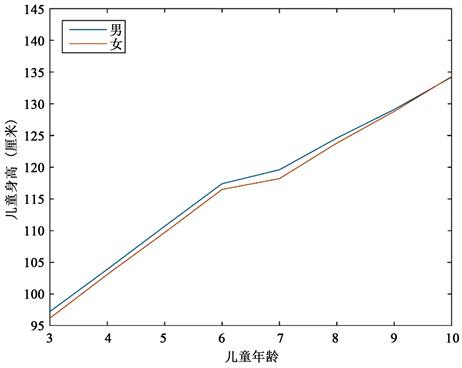
Figure 3. Broken line of height of children aged 3 - 10 in rural areas of China in 2015

图3. 2015年全国农村3~10岁男女儿童身高折线图

但由于收集到的数据便是各地区儿童的平均身高，并不能了解到更加详细的内容，所以在此处省略了其均值、方差，而进行了各组身高间的相关性分析，其中包括男女性别、城镇与农村、以及不同年份之间。其中大多序列相关系数都在0.99以上，从而我们可以初步地看出：对于不同年份、不同地区来说，儿童身高变化的趋势都是大致相同的。

3. 两总体的轮廓分析

为了通过数据来证明儿童身高较之前同龄的有所增加，在此次项目中，选择的研究方法是多元统计中的两总体轮廓分析。

设对同一个单元(个人、小块土地等)施加p种处理(如测验、问卷调查等)或在相继p个时间段内重复测量，依次得到测量值 $x_1,x_2,\cdots ,x_p$，其相应的均值依次为 ${\mu }_1,{\mu }_2,\cdots ,{\mu }_p$。将 $\left(1,{\mu }_1\right),\left(1,{\mu }_2\right),\cdots ,\left(1,{\mu }_p\right)$ 用直线连接起来的折线图，称为总体的轮廓。轮廓分析是轮廓的分析或多个轮廓的比较，它常用于分析比较相继一连串的心理测试或其他测试中。

设对两个总体的单位施加相同的p种处理， ${\mu }_1={\left({\mu }_{11},{\mu }_{12},\cdots ,{\mu }_{1p}\right)}^{\prime },{\mu }_2={\left({\mu }_{21},{\mu }_{22},\cdots ,{\mu }_{2p}\right)}^{\prime }$ 分别为总体1和总体2的p种处理的均值向量。按照两总体轮廓分析的思想方法，结合本次的课题，依次需检验的假设可包括如下两个：1) 对于不同地区或不同年份的儿童身高的两轮廓在外表上是相似的，或者更精确地说它们是平行的。2) 在假设1成立的基础上，即两轮廓的外表是相似的基础上，检验它们是不重合。

假设1的原假设就是

$H_{01}:\left(\begin{array}{c}{\mu }_{12}-{\mu }_{11}\\ {\mu }_{13}-{\mu }_{12}\\ ⋮\\ {\mu }_{1p}-{\mu }_{1,p-1}\end{array}\right)=\left(\begin{array}{c}{\mu }_{22}-{\mu }_{21}\\ {\mu }_{23}-{\mu }_{22}\\ ⋮\\ {\mu }_{2p}-{\mu }_{2,p-1}\end{array}\right)$

于是可将假设检验问题写为

$H_{01}:C{\mu }_1=C{\mu }_2,H_{02}:C{\mu }_1\ne C{\mu }_2$

其中

$C=\left(\begin{array}{ccccc}-1& 1& 0& \cdots & 0\\ 0& -1& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\end{array}\right)$

$\text{rank}\left(C\right)=p-1$

设两个独立样本 $x_1,x_2,\cdots ,x_{n_1}$ 和 $y_1,y_2,\cdots ,y_{n_2}$ 分别来自 $N_p\left({\mu }_1,\Sigma \right)$ 和 $N_p\left({\mu }_2,\Sigma \right)$ 则可知检验统计量为

$T^2=\frac{n_1{n}_2}{n_1\text{+}{n}_2}{\left(\bar{x}-\bar{y}\right)}^{\prime }{C}^{\prime }{\left(C{S}_p{C}^{\prime }\right)}^{-1}C\left(\bar{x}-\bar{y}\right)$

其中 $S_p$ 是 $\Sigma$ 的联合无偏估计。对于给定的 $\alpha$，拒绝规则为：

若 $T^2\ge T_{\alpha }^2\left(p-1,n_1+n_2-2\right)$，则拒绝 $H_{01}$

其中

$T_{\alpha }^2\left(p-1,n_1+n_2-2\right)=\frac{\left(p-1\right)\left(n_1+n_2-2\right)}{n_1+n_2-p}{F}_{\alpha }\left(p-1,n_1+n_2-p\right)$

当两总体的轮廓平行时，第1个总体的轮廓或者高于第2个总体的轮廓 $\left({\mu }_{1i}>{\mu }_{2i},i=1,2,\cdots ,p\right)$，或者低于第2个总体的轮廓 $\left({\mu }_{1i}<{\mu }_{2i},i=1,2,\cdots ,p\right)$，或者与第2个总体的轮廓重合 $\left({\mu }_{1i}={\mu }_{2i},i=1,2,\cdots ,p\right)$，三者必居其一。在此情形下，只有当两个轮廓的平均高度相同时，两轮廓才会重合。因此，假设2的原假设可写成

$H_{02}:\frac{{\mu }_{11}+{\mu }_{12}+\cdots +{\mu }_{1p}}{p}=\frac{{\mu }_{21}+{\mu }_{22}+\cdots +{\mu }_{2p}}{p}$

等价于考虑假设检验问题

$H_{02}:1^{\prime }{\mu }_1=1^{\prime }{\mu }_2,H_{12}:1^{\prime }{\mu }_1\ne 1^{\prime }{\mu }_2$

其中 $1^{\prime }=\left(1,1,\cdots ,1\right)$。

可知，假设2的检验统计量为

$T^2=\frac{n_1{n}_2}{n_1+n_2}{\left(\bar{x}-\bar{y}\right)}^{\prime }1{\left(1^{\prime }{S}_{p}1\right)}^{-1}{1}^{\prime }\left(\bar{x}-\bar{y}\right)=\frac{n_1{n}_2}{n_1+n_2}\frac{\left[1^{\prime }\left(\bar{x}-\bar{y}\right)\right]}{1^{\prime }{S}_{p}1}$

或

$t=\frac{1^{\prime }\left(\bar{x}-\bar{y}\right)}{\sqrt{\left(\frac{1}{n_1}+\frac{1}{n_2}\right)1^{\prime }{S}_{p}1}}$

对于给定的 $\alpha$，拒绝规则为：

若 $T^2\ge F_{\alpha }\left(1,n_1+n_2-2\right)$，则拒绝 $H_{02}$ ；

或

若 $\left|t\right|\ge t_{\alpha /2}\left(n_1+n_2-2\right)$，则拒绝 $H_{02}$。

4. 数据代入

通过对数据的收集与整理，我们可得到更加清晰的数据内容，其中部分数据 [12] 展示见表1。

Table 1. Part of the data presentation

表1. 部分整理数据展示

数据表格中第一列表示儿童的性别(其中B表示男孩，G表示女孩)；第二列说明的是儿童的各年龄段，在此次项目中，我们是从3岁到10岁的儿童中收集的数据；第三列指的是所在年份，例如在此次列出是来自2010年的数据；第四列表示的是各年龄儿童的平均身高；最后一列指的是数据所包含的区域，例如这列举出的部分是全国的儿童身高。

将数据代入两总体的轮廓分析中，可以的到相关的检验统计量。在假设1中，设立了两个检验。一个是对不同地区(城市和农村)的轮廓分析，此时计算出的检验统计量，即如表2所示。

Table 2. Test statistics for different regions in hypothesis 1

表2. 假设1中不同地区的检验统计量展示

另外一个是对不同年份的轮廓分析，计算出的检验统计量如表3所示。

Table 3. Test statistics of different years in hypothesis 1

表3. 假设1中不同年份的检验统计量展示

在假设2中，我们通过编程，得到了对不同年份轮廓的进一步分析结果，如表4所示。

Table 4. The test statistics in hypothesis 2

表4. 假设2中检验统计量展示

5. 数据分析

通过以上的数据结果，我们可以的到以下分析：

假设1中的拒绝规则为：

若 $T^2\ge T_{\alpha }^2\left(p-1,n_1+n_2-2\right)$，则拒绝 $H_{01}$。

第一个检验，其原假设为不同地区的儿童身高变化的轮廓外表上是平行的。因为此时得出的检验统计量0.3579和0.3906均明显小于42.8807，表明在显著性水平为0.05的情况下，不拒绝原假设，即认为城市和农村的儿童身高变化的轮廓是平行的。假设1中对年份的检验，其原假设为不同年份的儿童身高变化趋势的轮廓是相似的。在这个假设中得出的检验统计量分别0.0179、0.2095、0.0162、0.2288，同样均小于42.8807，我们认为也无法拒绝原假设，即认为不同年份的儿童身高变化趋势的轮廓是相似的。

在假设1的两个检验中，均说明了儿童身高变化的轮廓是相似的，在这样的基础上，我们便可以顺利的进行对假设2的检验，即检验不同年份儿童身高的轮廓是否重合，此时的拒绝规则为：

若 $T^2\ge F_{\alpha }\left(1,n_1+n_2-2\right)$，则拒绝 $H_{02}$。

通过编程出的结果中，可以看出在显著性水平 $\alpha$ 为0.01的情况下，检验统计量分别为1.3192、5.5320、1.1545、4.4446，都大于1.0603，表明此时的计算结果在检验拒绝域内，则拒绝原假设，即通过明确的数据说明了不同年份中儿童身高的轮廓是不重合的。

这样的假设检验，通过明确的数据说明了随着时代的变化，现在儿童的平均身高相比于以前同龄儿童的均有所增长，即它们的轮廓虽然相似却不能重合。而儿童享受免票或半票待遇，不是因为他们个头小，只是因为他们是孩子，理应享受特殊照顾，以展示社会的关爱 [8]。这也明确的表明如果现在还使用以前的儿童票的标准便会使部分儿童的权益受到损害，让他们不能享受到自己应有的，所以需要制定新的儿童票收取标准。

6. 结论

本次项目通过多元统计的方法，对收集到的数据进行了总体的轮廓分析，通过上方的结果可以明确看出在经济水平明显提高，儿童获得的营养程度越来越好的情况下，儿童的身高相比于以前同龄儿童的身高都是有所增加。同时通过上面的描述性统计得到的图形中也可以看出，在2010年就有部分10岁孩童的身高已经超过了1.4米。这些都能明显地说明：以前的儿童票制定标准已不能很好地保护儿童的权益。为了保障儿童福利，儿童票的收取标准亟待更新。

在本次项目中，所能获取的数据资源有限，缺少刚制定儿童票标准时的相关儿童身高数据，所以我们并不能了解此政策明确的制定依据，以及制定此政策的明确目的。同时，此次收集到的数据均属于各地区各年份儿童的平均身高，但其变化的具体区间并不确定。在这样的情况下，如果用统计学方法来具体确定儿童票标准，存在数据不足与标准片面的问题。最后，儿童身高会受到诸多因素的影响，在同龄儿童中，也可能出现过度偏高或较矮的情况。如果仅用统计学方法给出明确的儿童票身高区间，也会存在较多的问题。

相比之下，儿童票收取“双标准”，即身高和年龄兼顾的原则，如此更加能保障儿童的权益。

回顾以前时代，由于信息技术的不够发达，国家规定只有在儿童成年之后才能申办身份证。在这样的情况下，才有了儿童1.1米至1.4米半票的标准。而如今时代发达，信息流通，小孩在父母的监护下，可以拥有自己的便于携带的身份证。在这样的情况下，单凭儿童身高来确定是否让他们免票或者半票，已然不再合适。

身份证是对儿童年龄的最好证明，各门票对儿童的售出可以主要通过儿童的年龄来确定。依照以前的儿童票制定标准，可以看出其底限1.1米是对6岁左右的孩童进行限制的，而1.4米是对10岁左右的孩童进行限制的。所以在依据年龄时，可以让6岁以下的孩子免票，而同时让6岁至10岁的孩童购买儿童半票。

而当儿童身份证忘带或还未办理的情况下，儿童身高便成了辅助标准。近年儿童的身高相比于以前均有所增加，那么对于身高的标准也需在以前的情况下有所增加。正如部分铁道部门将儿童票标准提高到1.2米至1.5米，对于其他的门票也可适用。

通过这样的“双标准”政策，让每个儿童都可以更好地享受到自己应有的权益。

7. 不足与展望

相比于前人的对儿童票标准的建议提出，本文中增加了数据和理论的支持，从而更有说服力地表明儿童票的标准急需更新。

然而在本次项目中仍存在不足之处，获取的二手儿童身高的数据较少。由于以前信息技术的不足，对儿童身高的统计与储存有着一定的难度，所以收集到的数据大多是从2000年开始的。儿童身高的数据统计需要大量的时间和资金支持，所以大多数地区对这方面数据的统计都是定期(相隔4、5年)开展的，因此在这样的情况下，我们收集到的关于儿童身高的年份较少。在这样的情况下，对数据的分析存在一定的局限性。同时，对于学生来说能力有限，只能从各数据网中获得不同年份不同地区各年龄段儿童的平均身高，从而缺少大大数据的支持，无法得到更加明确的儿童身高变化区间，使数据的说服力减弱。同时本次项目中也缺少一手资料的收集与调查调查。

致谢

感谢2019年上海市大学生创新创业训练计划项目(项目编号201910273107，项目名称“基于多元统计的儿童票定价策略的更新研究”)的资助。

基金项目

本文为2019年上海市大学生创新创业训练计划项目“基于多元统计的儿童票定价策略的更新研究”(项目编号201910273107)的研究成果之一。