基于电子健康档案中异构时态数据的学习

Learning from Heterogeneous Temporal Da-ta Based on Electronic Health Records

摘要: 电子健康档案包含大量的纵向数据，对于生物医学信息学研究很有价值。然而，由于数据的复杂结构，包括随时间不均匀分布的临床事件，对标准学习算法提出了挑战。时态数据建模的一些方法依赖于从时间序列中提取单一值，导致有潜在价值时序信息的丢失。因此，如何更好地解释临床数据的时效性，仍然是一个重要的研究问题。本文研究了电子健康档案中时态数据新的表示方法，这些表示保留了时序信息，并且可以由标准机器学习算法直接处理。基于时间序列数据符号化表示的研究方法有多种不同的方式。使用电子健康档案真实数据库中临床测量的数据集的实证研究结果表明，相比使用原始序列或聚类序列，对随机子序列使用距离度量显著提高了预测性能。本文提出的表示方法更好地解释了临床事件的时效性，对于生物医学领域的预测任务十分关键。

Abstract: Electronic health records contain a large number of longitudinal data, which is valuable for biomedical informatics research. However, standard learning algorithms present challenges due to the complex structure of the data and clinical events that are unevenly distributed over time. Some methods of temporal data modeling depend on extracting single values from time series, which leads to the loss of potentially valuable sequential information. Therefore, how to better explain the temporality of clinical data is still an important research question. In this paper, a new representation of temporal data in electronic health records are studied, which preserves the sequential information that can be processed directly by the standard machine learning algorithms. The research method based on time-series data symbol representation has many different ways. Empirical studies using clinically measured datasets in the real-life database of electronic health records have shown that using distance metrics for random subsequences significantly improves predictive performance compared to the use of original sequences or clustering sequences. The representation method proposed in this paper better explains the temporality of clinical events and is key to the prediction task in the biomedical domain.

1. 引言

电子健康档案(Electronic Health Records, EHRs)包含日常临床活动中获得的大量纵向数据。在EHRs中可以获得各种各样的数据类型，系统地收集EHRs数据为通过增强错误检测、提高依从性和降低成本来改善临床护理提供了可能性，质量测量、公共卫生监测和患者获得健康状况的数据是EHR系统最直接的好处 [1]。EHRs的使用促进了生物医学信息学从个体层面向人群层面转变的机会，这在临床和转化研究中受到越来越多的关注 [2]。

与传统的基于叙述的健康档案相比，EHRs中综合病人病史构成了表型特征的可计算集合，这在很大程度上促进了人口层面的知识发现。同时使用EHRs使得数据的异构类型提供了患者的整体视角，其中每位患者的唯一ID连接来自不同临床科室的数据，随时间收集的临床数据为患者提供了临床事件的轨迹，因此可以进行纵向分析，这对于生物医学信息学研究很有价值。

目前，EHR数据的分析主要分为四类：共病性、患者聚类、机器学习和队列查询 [3]。其中，机器学习作为一种从大量EHR数据中获取有用信息的方法受到了广泛的关注。机器学习算法利用统计理论从训练数据中建立计算模型，并做出可应用于测试数据的推论。通常要求训练数据和测试数据都采用特定的格式，即表格格式，其中对象或示例构成行，描述这些行的特性或属性构成列。但在不损失关键信息的条件下，EHR数据很少直接符合这种格式，这主要是由于纵向观测的普遍性，即对象不是由具有单个值的一个特征来描述，而是由一段时间内的一系列值来描述。图1说明了将EHR数据转换成表格格式的问题。通常情况下，一位患者在一定时间内连续不断地报道某些临床测量结果，因此，这些临床测量是结果数据表的相应单元中的一个时间序列。此外，由于每位患者的轨迹都是唯一的，因此这些时间序列通常具有不同的长度，并且以不规则的时间间隔进行测量。标准机器学习算法不能直接从这种复杂的数据表中构建预测模型，原因主要有两方面：1) 大多数学习算法只能处理包含单个数值或分类值的特征；2) 如果没有参考点，例如给定的查询，大多数学习算法很难比较不同对象的相似程度。因此解决由不同长度和以不规则间隔测量的异构时间序列所增加的复杂性问题十分重要。

如图1所示，将原始EHR数据转换为用标准机器学习算法直接处理的表格格式时，问题归结为生成表示时间序列的特征。对这一方向已经进行了许多研究 [4] [5] [6]。然而，与以前的研究不同，本研究试图处理如图1所示的数据表，其中包含从结构丰富的EHR数据中提取用于分类的不同长度的时间序列。本研究以检测不良药物事件(ADES)为研究对象，这是一个重大的公共卫生问题。近年来，EHR数据已成为药品安全监测的宝贵资源。EHRs不仅具有传统数据来源的优势，而且还提供了与不患有ADES的患者形成对照组的可能性。后者尤为重要，因为它允许关联估计，并为有监督的机器学习提供类标签。挖掘用于ADE检测的结构化和非结构化EHR数据的研究尚处于起步阶段 [7] [8]。在EHRs中用于ADE检测的大多数方法没有考虑到临床事件的时效性，但这对预测任务至关重要。

Figure 1. Illustration of the complexity when extracting EHR data

图1. EHR数据转换成表格格式示意图

2. 相关工作

为了分析时间序列数据，SAX表示已广泛用于单变量和多变量时间序列 [9] [10]。与本研究中描述的问题密切相关的是，一些研究使用SAX表示从时间序列数据中创建特征。为了将时间序列数据转换成表格格式，Hills等 [11] 提出了一种单扫描shapelet变换算法，该算法从一组单变量时间序列中寻找最佳k个shapelet，然后将原始时间序列数据转换为具有k个特征的数据集，每个特征都是该序列与一个shapelet之间的距离。这样，任何标准学习算法都可以处理变换后的数据集。Gordon等 [12] 引入了shapelet采样算法，用于基于shapelet分类树的快速计算，对随机子序列进行采样和评估，并计算信息增益。Karlsson等 [13] 提出了随机shapelet森林算法，该算法在生成森林中的树时，生成多个shapelets，并在每个节点上选择最好的一个。该方法在保持预测性能的同时，显着地降低了计算成本。

受前面这些方法的启发，我们提出了基于随机子序列的方法处理图1所示的数据表。首先应用SAX表示从一组时间序列中获得对应于每个特征的符号序列；然后，在每个特征下，随机地生成多个子序列，从中选出信息量最丰富的子序列；最后，将每个时间序列替换为与所选子序列的编辑距离。此时，任何类型的分类器都可以处理变换后的数据集，生成预测模型受前面这些方法的启发，我们提出了基于随机子序列的方法处理图1所示的数据表。首先应用SAX表示从一组时间序列中获得对应于每个特征的符号序列；然后，在每个特征下，随机地生成多个子序列，从中选出信息量最丰富的子序列；最后，将每个时间序列替换为与所选子序列的编辑距离。此时，任何类型的分类器都可以处理变换后的数据集，生成预测模型。

3. 基本概念

时间序列 $T=\{t_1,\cdots ,t_n\},t_i\in R,\forall i\in \left[1,n\right]$ 是在一个时间周期内进行的n个度量的有序集合，通常对应于一个时间演化变量。给出固定参数w，时间序列T可以由实向量 $\bar{T}=\left\{\overline{t_1},\cdots ,\overline{t_w}\right\}$ 表示在w维空间中，其中 $\bar{T}$ 的第i个元素计算如下：

$\overline{t_i}=\frac{w}{n}{\displaystyle \underset{j=\frac{n}{w}\left(i-1\right)+1}{\overset{\frac{n}{w}i}{\sum }}{t}_j}$ (1)

通过将每个时间序列分割成大小相等的w段，原始时间序列表示从n维降到w维。每段被分配一个新的值，该值对应于属于该段内的序列的平均值。这种表示被称为分段聚合近似表示(Piecewise Aggregate Approximation, PAA) [14]。

给定时间序列T，应用PAA获得 $\bar{T}$ ，通过将 $\bar{T}$ 的每个值映射到使用高斯分布定义的离散符号获得 $\bar{T}$ 的离散表示。更确切的说，定义一组 $\alpha -1$ 个分割点 $B=\{{\beta }_1,\cdots ,{\beta }_{\alpha -1}\}$ ，其中 $\alpha$ 是字母表大小，使得高斯正态曲线下每对 $\left({\beta }_i,{\beta }_{i+1}\right)$ 对应的面积都等于 $1/\alpha$ 。为了完整性，假设 ${\beta }_0=-\infty ,{\beta }_{\alpha }=\infty$ 。因此，给定所需的字母表大小 $\alpha$ ，通过查阅统计表可以很容易地定义分割点。

得到分割点后， $\bar{T}$ 中的PAA系数将映射得到符号 $\widehat{\stackrel{¯}{T}}$ 序列，具体如下：低于第一个分割点的所有系数都映射到第一个字母表符号，例如a；将第一个和第二个分割点之间的下一组系数值映射到第二个符号，例如b；以此类推。由此产生的离散序列表示称为符号聚合近似表示(Symbolic Aggregate Approximation, SAX) [15] [16]。

对于一个长度为w的离散事件序列X，X的子序列S被定义为X中连续符号长度为l的抽样，使得 $l\le w$ ，即 $S=\{x_q,\cdots ,x_{q+l-1}\},l\le q\le w-l+1$ 。设 $D(\cdot )$ 是两个长度相同的离散事件序列的距离函数。给定长度为w的目标序列X和长度为l的序列S， $l\le w$ ，S到X的距离函数 $D(\cdot )$ 定义如下：

$Dist\left(S,X\right)=\underset{\forall S^{\prime }\subseteq ,\left|S^{\prime }\right|=l}{\min }\left\{D\left(S^{\prime },S\right)\right\}$ (2)

其中 $S^{\prime }$ 是长度为l的时间序列X的子序列。 $D(\cdot )$ 可以是字符串匹配的任意距离函数，本研究使用编辑距离 [17]，也被称为Levenshtein距离。

使用上述距离函数，定义随机序列子序列(sequence shapelets)的概念。考虑由K类组成的离散序列数据集D，设 $P\left(C_i\right)$ 为属于类 $C_i$ 的序列的比例， $\forall i\in \left[1,k\right]$ 。D的熵定义为：

$I\left(D\right)=-{\displaystyle \underset{i=1}{\overset{k}{\sum }}p\left(C_i\right)}\log \left(p\left(C_i\right)\right)$ (3)

将D划分为m个不相交的子集 $D_1,\cdots ,D_m$ ，D的总熵定义为：

$\hat{I}\left(D\right)=-{\displaystyle \underset{i=1}{\overset{m}{\sum }}\frac{D_i}{\left|D\right|}I\left(D_i\right)}$ (4)

因此，数据集D上特定分区策略sp的信息增益定义为：

$Gain\left(D,sp\right)=I\left(D\right)-\hat{I}\left(D\right)$ (5)

基于时间序列子序列 [18] 的原始定义，我们将随机序列子序列定义为D中所有子序列中信息增益最高的离散事件子序列。利用等式(3)~(5)，Shapelet S的信息增益 $SGain(\cdot )$ 计算如下：

$SGain\left(S\right)=\underset{sp\in D}{\max }Gain\left(D,sp\right)$ (6)

4. 数据分析方法

本节详细描述所提出的方法。首先介绍从时间序列中生成符号序列，然后介绍使用生成的符号序列作为特征进行分类的四种策略：1) 原始序列；2) 聚类序列；3) 随机子序列；4) 随机动态子序列。

4.1. 序列生成

为了使时间序列更容易由分类器直接处理，我们使用SAX表示将每个时间序列转换为字符串(图2)。在SAX表示算法中需要设置两个参数：维数(w)和字母表大小(a)。第一个参数w是时间序列被划分为大小相等的分段数目，而a是用来映射所有分段中标准化时间序列值的符号数。在本研究中，我们考虑a值为2、3和5，2个符号反映高和低(或，正常和异常)，3个符号增加一个中间范围，5个符号考虑一个更精确的系统，其中基本时态信息损失更少。通过将SAX表示应用于每个特征，由异构时间序列组成的数据集转换为包含不同长度序列的数据集，可以通过标准分类器直接处理。

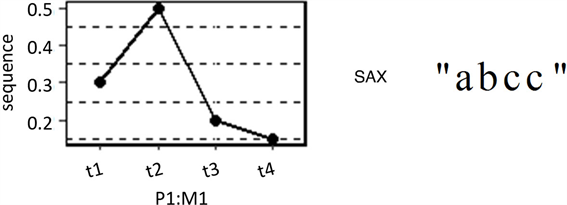
Figure 2. Sequence generation from time series using the SAX representation

图2. 使用SAX表示从时间序列生成序列

4.2. 序列聚类

通过将上述序列生成方法应用于每个时间序列，得到的数据集包含不同长度的序列作为特征。当同一特征中的大多数序列是不同的时，直接使用它们进行分类可能不会产生有意义的结果，因为无法在测试集中的序列与训练集中的序列之间找到匹配。为了减少一个特征中的序列多样性，一种解决方案是将它们进行分组，这样具有相似符号特征和/或符号数目的序列就会分为同一类别。为此，我们使用分区聚类，更具体地说是围绕中心点的划分(PAM)算法 [19] 对原始序列进行聚类。PAM算法寻找k个有代表性的中心点——类中的对象与所属类中其他所有对象之间的平均相异度度量最小——通过将每个对象分配到与其最近的中心点来构建k个类别。在本研究中，对象是通过SAX表示生成的序列。每个序列代表一个临床测量的记录，即在规定的时间段内由一个病人得到的变量。它类似于k-均值聚类算法，但更健壮，因为它允许使用任何类型的距离度量，并最小化每对差异度度量的总和，而不是平方欧几里德距离的总和 [20]。将数据集划分为k个类别之后，属于同一类别的序列被其中心点代替用于构建预测模型。

Algorithm 1. Random subsequence selection

算法1. 随机子序列选择

4.3. 随机子序列选择

在本研究中，我们提出了一种减少特征中序列多样性的替代方法。在这里，我们的目标是找到一个子序列，该子序列表示来自同一个类的序列共享的公共符号对齐，并将其与其他类别区分开来。通过使用子序列，具有不同长度的原始序列的问题得到解决，因为长度不同的两个序列只要有相同的代表性子序列，相互之间就是有关的。

对于每个特征，首先使用随机生成的子序列将特征从序列向量转换为原始序列与生成子序列之间的距离向量。这种子序列是从该特征中现有的单个元素创建的，其随机长度不超过最长的原始序列。使用基于等式(3)-(5)的信息增益(IG) [21] 评估所生成的子序列。在所生成的子序列中，选择IG最高的子序列，然后将特征转化为与原始序列之间的距离。本研究中使用的距离度量是编辑距离 [12]，它根据将一个字符串转换到另一个字符串所需的单个字符编辑–插入、删除或替换的最小数量计算。给定由n个不同序列s组成的特征f，算法1给出了随机子序列选择的详细实现步骤。在本研究中，n_iter被设置为10000，充分覆盖每个特征中给定的不同序列数的潜在子序列。

4.4. 随机动态子序列

通过用可变的字母表代替固定不变的字母表大小扩展了随机子序列模型，因为并不是所有的时间序列都必定遵循相同的变化。在本研究中，我们使用算法为每个临床测量动态地分配最合适的a值。通过将不同a值(2、3和5)的SAX表示应用于每个临床测量，然后从使用不同a值创建的序列组中选择一个最优的子序列来实现，这种方法称为随机动态子序列。算法2给出了详细的算法实现步骤。

Algorithm 2. Random dynamic subsequence

算法2. 随机动态子序列

5. 实证研究

在本节中，我们通过对药品不良事件检测的实证研究，验证能否通过应用基于随机子序列的方法来提高预测性能。首先介绍数据集，然后对所提出的方法进行一系列的实验验证和评估，最后给出预测性能的评价指标。

5.1. 数据集

对于训练模型，实验使用Adadelta [22]，预处理后共有72个样本，其中阳性样本数11个，阴性样本数61个。我们以0.75:0.25的比例将数据集随机划分为训练和测试集。训练集用于模型拟合的数据样本，测试集用来评估最终模型的泛化能力。

5.2. 实验

在本研究中，设计了一系列的实验来研究所提出的方法在分类任务中处理异构时间序列作为特征的影响。

第一个实验评估三组9个模型的预测性能。每组包含a值为2、3和5的SAX表示得到的数据集。第一组模型使用SAX表示得到的序列作为特征，用原始序列表示；第二组模型使用序列聚类得到的中心点作为特征，用聚类序列表示；第三组以序列与其对应的随机子序列之间的编辑距离作为特征，用随机子序列表示。

第二个实验将使用随机动态子序列算法产生特征的模型与将序列长度作为特征的模型进行比较。序列长度是指序列中符号的数量，不考虑时间序列的序列信息。先前研究认为，在EHRs中用于ADEs检测的临床测量中，序列长度是最优的将时间序列概括为单个值的表示 [23]。

后续实验通过变量重要度分析对随机动态子序列模型进行研究，得到使用不同a值生成的子序列中，最好的代表相应临床测量动态表示的子序列。分析不同a值在所有临床测量中的分布，以及在信息最丰富的测量中的分布。

5.3. 评估

采用随机森林算法 [24] 作为底层分类器评估所提出的方法。由于数据集的分类不平衡，本研究中使用的性能评估指标是ROC曲线下的区域(AUC) [25] [26]。ROC曲线代表敏感性(真阳性率)和1-特异性(假阳性率)之间的一种权衡，前者衡量有多少阳性被识别为阳性，后者衡量有多少阴性被识别为阳性。分析ROC曲线的一个常用方法是计算AUC。本研究使用的另一个评估指标是F1测量。F1值是精确率和召回率的调和均值，是精确率和召回率的综合评价指标。

5.4. 结果

本节给出实施的一系列实验对应的结果。

Table 1. Results of random forest models using Original Sequence (OS), Sequence Cluster (SC) and Random Subsequence (RS)

表1. 原始序列(OS)、序列聚类(SC)和随机子序列(RS)的随机森林模型的结果

5.4.1. 比较原始序列、聚类序列和随机子序列

使用字母表大小a分别为2、3和5的原始序列、聚类序列和随机子序列这三种方法建立了9个预测模型。表1给出了预测性能结果的总结。可以看出，对于选定的a，模型的选择对预测性能产生一定的影响。总体来说，使用随机子序列模型可以获得最好的预测性能。然而，对于选定的模型，没有迹象表明一个特定的a值在所有模型中是最有效的。因此使用随机动态子序列方法，该方法为数据集中的每个特征寻找最合适的a值。

5.4.2. 比较随机动态子序列与序列长度

分别使用随机动态子序列和序列长度创建特征的随机森林模型的结果见表2。显然，前者的使用明显优于后者，尽管序列长度在以前被认为是同一任务中此类数据的最佳单值表示形式。相比于序列长度，使用随机动态子序列方法时，AUC提高了11%，F1提高了31%。

根据基尼重要性评分计算每个特征的变量重要度后，可以对所有特征进行相应的排序。由于每个特征只包含由一个a值获得的序列，因此可以对所有特征的a选择的分布进行总结。图3以定量和定性的方式说明了a的选择。定量地(左图)显示每个a值在所有特征中所占的比例。定性地(右图)，根据变量的重要性得分对a进行相应的排序。结果表明，数据集的较多特征都是通过a值为2的SAX表示进行转换的。

Table 2. Results on comparing Sequence Length (SL) with Random Dynamic Subsequence (RDS)

表2. 序列长度(SL)与随机动态子序列(RDS)的比较结果

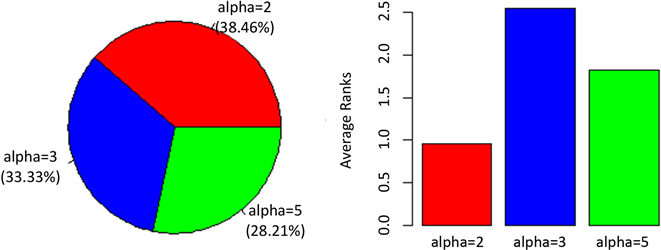
Figure 3. Distribution of a values among all features and the corresponding average ranks according to their variable importance

图3. a值在所有特征之间的分布，并根据变量的重要性得分对其进行相应的排序

6. 总结

电子健康档案包含大量纵向、时间戳的临床数据，用机器学习算法处理此类数据通常需要将其转换为表格格式。本研究提出了一种基于子序列的时间序列符号化表示方法。该方法允许直接应用任何标准机器学习算法，同时与基于单一表示的方法相比，它在一定程度上能够获取时序信息，因而显著地提高了预测性能。

基金项目

国家自然科学基金项目(61572442)；福建省高校创新团队发展计划，福建省研究生导师团队，泉州市高层次人才团队项目(2017ZT012)；华侨大学研究生科研创新基金资助项目。