1. 引言
随着经济全球化,供应链决策面临越来越多的挑战。目前,许多学者在需求不确定的情况下对供应链协调问题进行了大量的研究。但是,在供应链决策中,除需求不确定性外,还会面临其他影响因素。首先,生产存在不确定性,比如:农产品的产量和温度、降水等。其次,供应链成员的风险态度也影响决策。因此,在生产和需求不确定的情况下,结合成员风险态度研究供应链协调是十分有必要的。
近年来,除需求不确定外,供应不确定也引起了学者的重视。比如He Xu等 [1] 研究表明期权契约可以实现供应链协调;Yong He等 [2] 说明制造商和零售商采用批发价合同和退货策略,可以实现供应链协调;M. Güray Güler [3] 等研究表明产量的随机性并不改变批发价、回购、收益分成、数量折扣和数量弹性契约的协调能力,但是影响契约参数的取值;Fei Hu等 [4] 发现收入共享政策与订单罚款和回扣(OPR)契约,可以充分协调供应链;最后,给出了数值算例。张文杰等 [5] 通过期权契约与其他契约的比较,说明了期权契约不仅可以实现供应链协调,还可以提高供应链绩效;罗军 [6] 研究表明回购契约可以实现供应链协调;罗加蓉 [7] 通过分别构建看涨期权、看跌期权和双向期权契约下的供应链博弈模型,研究了现货市场和期权契约市场共存下产出和需求双边随机供应链的订购、生产和协调优化决策;Nosoohi Iman等 [8] 研究表明通过期权契约可以减少成本不确定性的影响,最终实现供应链协调;Jiarong Luo等 [9] 发现收益共享契约与盈余补贴机制相结合,可以协调供应链,同时通过选择合适的参数,可以实现供应链利润在两个企业之间任意分配;郑佳琳 [10] 建立单一订购期权契约和混合订购期权契约下Stackelberg博弈模型,运用逆向归纳法求解供应商的最优生产投入策略和零售商的最优订购策略,并探讨了不同契约模式下供应商和零售商的期望利润;聂腾飞 [11] 的研究表明合理的政府补贴可以使批发价格契约实现供应链协调;李小美等 [12] 设计了回购和成本分担契约,不仅能协调供应链,还可以实现供应链利润的自由分配。但是,这些研究都是在零售商和供应商是风险中性条件下进行的。
在实际生产中,供应链成员面临各种因素造成的风险,这些风险除造成经济损失外,还会对决策者的心理产生影响,进而影响其决策行为。比如,因需求不确定造成库存积压,零售商承担经济损失的风险,同时对其心理产生影响,导致其减少订购量等。实际上,一些学者已经开始研究供应链成员风险态度对供应链协调影响。在已有的文献中,一般运用效用函数来衡量风险大小,常用的有分段线性效用函数、基于CVaR准则效用函数等,比如Weiwei L等 [13] 运用分段线性效用函数,研究了损失规避的零售商和风险中性的供应商组成的供应链协调问题,结果表明,回购(BB)和数量弹性(QF)合同可以协调供应链,而批发价契约不能实现供应链协调;许明辉等 [14] 运用分段线性效用函数,研究了收益共享契约和回购策略对供应链的协调作用;罗伟伟等 [15] 运用分段线性效用函数,研究损失厌恶的零售商的供应链契约协调设计问题;许民利等 [16] 应用CVaR准则效用函数,探讨收益共享契约下供应链协调的条件。上述研究表明,当零售商是风险厌恶时,供应链的决策受到影响,仍然可以采用适当的契约使供应链协调。在实际生产中,供应不确定导致订购量不能满足,供应商也承担损失的风险。因此,在供应和需求不确定条件下,研究供应商和零售商同时是风险厌恶的供应链协调问题是十分必要的。
近年来,由著名心理学家萨勒提出的“心理账户”理论被用于成员具有风险态度的供应链协调研究中,例如:杨旭瑞 [17] 运用多重心理账户理论来描述货代的风险态度,研究了风险中性航运企业和损失规避货代所组成的供应链在期权契约下货代的联合决策问题。本文的目的是应用心理账户理论研究供应商和零售商都是风险厌恶的供应链协调问题。首先,利用心理账户理论,将供应链成员的收入、支出分别计入收益、损失两个不同账户,然后,利用“罚函数”思想,通过对损失账户进行惩罚,构建一个新的效用函数,表示供应链成员的风险厌恶程度。最后,通过分析新的效用函数下的供应链成员的决策,研究供应链的协调问题。
2. 问题与基本假设
本文考虑一个风险厌恶的供应商、一个风险厌恶的零售商和一种产品组成的二级供应链系统。供应商生产产品,零售商向供应商订购产品,在市场销售,零售商面临的市场需求x不确定,取值区间为 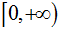 ,其分布函数和概率密度函数分别为
和
,且
是严格单调递增和可导的函数,均值为
。记
。供应商面临产品生产率y是不确定的,取值区间为
,其分布函数和概率密度函数分别为
和
,且
是严格单调递增和可导的函数,均值为
。记
。供应商面临产品生产率y是不确定的,取值区间为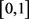 ,其分布函数和概率密度函数分别为
和
,且
是严格单调递增和可导的函数,均值为
。假设x与y是相互独立的,且供应商的实际产出低于零售商的订购量q时,供应商需要从现货市场购买产量不足的部分,为如期交货。
,其分布函数和概率密度函数分别为
和
,且
是严格单调递增和可导的函数,均值为
。假设x与y是相互独立的,且供应商的实际产出低于零售商的订购量q时,供应商需要从现货市场购买产量不足的部分,为如期交货。
本文建模时用到下面的记号:
R:供应商的计划生产量
c:供应商的单位生产成本
w:产品的单位批发价格
q:零售商的订购量
p:产品的单位零售价格
v:现货的单位价格
s:零售商的单位缺货损失
:零售商的风险厌恶系数
:供应商的风险厌恶系数
为了符合实际和简化计算,模型基本假设:
(a) 不失一般性,
;
(b)
;
(c)
;
(d) 当实际产品低于订购量时,供应商采购现货补足至订购量q,当实际产品高于订购量时,零售商仅接受数量为q的产量。
本文根据Bellantuono [18] 的研究结果,运用多重心理账户表示零售商和供应商的风险厌恶程度,分别为零售商和供应商建立两个心理账户,即收益账户(Ra)和损失账户(La),其中:收益账户记录零售商和供应商通过销售产品获得的收益,损失账户记录零售商缺货造成的损失和供应商采购现货造成的损失。
为了表示供应商和零售商的风险厌恶程度,本文采用下面的效用函数:
,其中,
为风险厌恶系数,
,
值越大,意味着对损失的厌恶程度越高,反之,意味着对缺货的厌恶程度越低。当
时,零售商和供应商是风险中性的,效用函数表示的是零售商和供应商的利润函数。因此,运用心里账户可以将效用函数和利润函数建立联系。
本文采用Stackelberg博弈模型建模。假设零售商是领导者,供应商是跟随者。供应链的运作方式如下:第一阶段即在销售期前,零售商根据市场随机需求和历史订单量确定订购量为q,供应商根据零售商的订购量决定计划生产量
,然后开始生产,实际产量为
,其中y是随机生产率,第二阶段即生产完成后,零售商根据供应商的生产量确定最优订购量
,供应商将产品运送给零售商,零售商将产品销售给顾客。如果不能满足市场需求,零售商产生缺货损失;销售结束时,剩余产品的残值为零。
本文的目的是研究供应链协调问题。在本文中,称一个契约协调供应链是指:应用该契约,使得下面条件成立:
1) 集中式供应链的期望利润最优;
2) 分散决策下,零售商和供应商的期望效用最优。
3. 集中式供应链模型
在集中式供应链中,供应商和零售商是一个整体,假设供应链的领导者是风险中性的,决策的目标是极大化供应链系统的期望利润,即寻求供应商和零售商的期望利润之和最大。
供应链系统的期望利润为
其中:第一项表示的是销售收入,第二项采购现货的成本,第三是缺货损失,第四项是生产的成本。
命题1 在随机产出随机需求条件下,供应链系统利润
是关于
的联合凹函数,当
时,最优订购量
和最优计划生产量
存在且满足
(1)
其中
由下式确定
(2)
证明:对 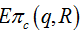 分别求关于q和R的一阶偏导数得
分别求关于q和R的一阶偏导数得

当
时,定义函数
则
,
。由假设(c)可得到:
,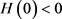 ,因此,
存在唯一解
。
,因此,
存在唯一解
。
令
,将
代入方程
,得到
(3)
记上式左边式子为
。因为
和
是分布函数,由假设得到
根据根的存在定理可知,方程(3)存在唯一解,记为
,则
满足
于是,供应商的生产量为
。
求关于q和R的二阶偏导数得
于是,
的Hesse矩阵为:
所以,Hesse矩阵为负定矩阵,即函数
是关于
的凹函数。又因为
是满足一阶条件的点,所以
是零售商的最优订购量和供应商的最优生产量。
4. 批发价契约下的情形
在分散式供应链中,风险厌恶的供应商和风险厌恶的零售商是不同的经济体,决策的目标是使其各自的效用最大化。
4.1. 供应商的决策
首先,供应商根据零售商的订购量q来计划生产量为R,实际产量为yR,当产量小于订购量时,采购现货补足,购买现货的数量为
。供应商的收益是销售收入与生产成本之差,其损失为采购现货成本。供应商的收益
和损失
为
其效用函数为
,即
其中
是供应商的风险厌恶系数,
。供应商的期望效用函数为
命题2当零售商的订购量为q时,供应商的最优计划生产量
,其中
满足
(4)
证明:经计算一阶导数到
当
时,定义函数
因为
,
, 由假设(c)可得到:
,
,所以,根据根的存在定理可知,
存在唯一解
。
令
,将
代入方程
,得到
满足(4)。
由
及
。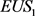 是关于R的凹函数,所以,当零售商的订购量
是关于R的凹函数,所以,当零售商的订购量
为q时,供应商的最优计划生产量
。
4.2. 零售商的决策
零售商收到产品的数量为q,其收益为销售收益,即销售收入减去采购成本,
零售商的损失为缺货损失,即
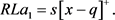
于是,零售商的效用函数为
,即
其中
是零售商的风险厌恶系数,
。零售商的期望效用函数是
命题3 在批发价契约下,零售商的最优订购量存在且满足
(5)
证明:对
关于q的一阶导数得:
由假设(d),
且
,则方程
存在唯一解,记为
,且满足
。
又因为
,及
知道 EUR1 是关于q的凹函数,所以,在批发价契约下,零售商的最优订购量存在且满足(5)。
根据命题2和3可以得到,供应商的最优生产量为
,其中
满足(4)。
简单计算可以得到以下结论:
结论1 供应商的最优计划生产量
随着风险厌恶系数
,现货成本v的增加而增加;随着成本c的增加而减少。
结论2 零售商的最优订购量
随着风险厌恶系数
,单位缺货损失s,零售价格p的增大而增大;随着批发价w的增大而减小。
因为
,由(2)和(4)得到
。再由(1)和(5)得到:无法通过调整批发价w使得供应链协调。因为即使选择适当的批发价w使得
,仍然无法保证
成立。因此,单一的批发价契约无法使供应链协调。
5. 回购–成本损失分担契约
根据假设,在随机产出的环境下,当产出量超过订购量时,供应商产生积压损失;而当产出量不能满足的订购量时,供应商从现货市场够买补足,产生缺货损失。为了协调供应链,一方面,为激励供应商满足零售商的订购量,零售商分担供应商的缺货损失,损失分担系数为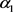 ,
,且分担供应商的生产成本,成本分担系数为
,
。另一方面,为了鼓励零售商多订货,在销售季节末,供应商以单位回购价格b回购零售商剩余产品,从而降低零售商因订购过多而产生的损失。
,
,且分担供应商的生产成本,成本分担系数为
,
。另一方面,为了鼓励零售商多订货,在销售季节末,供应商以单位回购价格b回购零售商剩余产品,从而降低零售商因订购过多而产生的损失。
5.1. 供应商的决策
假设零售商的订购量是q,供应商决策使其利润最优计划生产量R。供应商的收益是销售收入减去生产成本和回购费用,其损失为采购现货成本。供应商的收益
和损失
为
其效用函数为
,即
其中
是供应商的风险厌恶系数,
。供应商的期望效用函数为
(6)
命题4 当零售商的订购量为q时,如果
成立,供应商的最优计划生产量
,且
满足
(7)
证明:经计算,
当
时,定义函数
则
,
,由
可得到:
,
。因此,
存在唯一解
。
令
,将
代入方程
,得到k2满足(7)。
由
及
,
是关于R的凹函数,所以当零售商的
订购量为q时,供应商的最优生产量满足
。
5.2. 零售商的决策
零售商的收益
为销售收入加上回购收入,再减去采购成本、分担的部分生产成本及分担供应商的部分损失,即
零售商的损失
为缺货损失,即
于是,零售商的效用函数为
,即
其中
是零售商的风险厌恶系数,
。零售商的期望效用函数是
(8)
命题5 在联合契约下,当
且
(9)
时,零售商的最优订购量
满足
(10)
证明:将
代入
,求关于q的一阶导数得:
将上式右边记为
。因为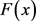 是分布函数,所以
是分布函数,所以
,
,
当(9)成立时,
且
,于是方程
存在唯一解
满足(10)。
由
是分布函数及
,
是关于q的凹函数。
于是,在联合契约下,零售商的最优订购量
满足(10)。
根据命题4,5可以得到,供应商的最优订购量为
。
简单计算可得下面结论:
结论3 供应商的最优计划生产量
随着风险厌恶系数
和现货成本v的增加而增加;随着成本c,损失分担系数
和成本分担系数
的增加而减少。
结论4 零售商的最优订购量
随着风险厌恶系数
,单位缺货损失s,零售价格p、回购系数b的增大而增大;随着批发价w,损失分担系数
和成本分担系数
的增大而减小。
5.3. 供应链协调
命题6 如果参数
满足
(11)
且
(12)
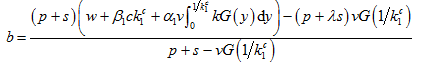 (13)
(13)
则在联合契约下,供应链可以实现协调。
证明:根据定义,要协调供应链,必须有:
和
。
由
和
,命题1,4和5,得到:
。
由
,命题1和5得
(14)
由
,命题1和4得
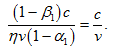 (15)
(15)
整理即得(12)和(13)。
因此,当参数
满足(11),(12)和(13)时,供应链系统的期望利润达到最优,且供应链和零售商的期望效用最优,即供应链实现协调。若要供应链实现完美协调,还应该调整联合契约参数,使得供应链成员的期望利润不低于保留值。
根据简单计算可得:
结论5 当风险厌恶系数
和
给定时,
关于
的增大而增大,b关于
的增大而增大。
结论6 其他条件不变时,
关于风险厌恶系数
的增大而增大,b关于风险厌恶系数
的增大而减小。
5.4. 数值算例
模型参数
,
,
,
,
。假设市场需求x服从
上的均匀分布,生产率y服从
上的均匀分布,
,
,
,
,
,
。
在集中决策下,零售商的最优订购量
,供应商的最优生产量 ,供应链系统的最优期望利润是
。在批发价契约(
,供应链系统的最优期望利润是
。在批发价契约( )下,零售商和供应商的期望利润分别为
和
。
)下,零售商和供应商的期望利润分别为
和
。
首先,验证命题6的结论。取
,
。在回购-成本损失分担契约下,将模型参数代入(11),(12)和(13),经计算知:契约参数
的满足
,
且
.
让
在
取的值,分别计算
,b,
,
,零售商和供应商的期望利润(
和
)及期望效用(
和
),得到
,
,其余结果如表1所示。

Table 1. The impact of contract coefficients on the expected utility and expected profits of supply chain members
表1. 契约系数对供应链成员期望效用和期望利润的影响
由表1可以看到:参数满足命题6的条件时,
与
之和等于3401.6035,即
。因此,供应链得到协调。还可以看出:随着
的变大,
和b逐步变大,
和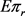 逐步减少,
和
逐步增加,即在协调的情况下,当成本分担系数增加时,损失系数和单位回购价也增加,零售商期望效用和期望利润逐步减少,而供应商的期望效用和期望利润则逐步增加。因此,要实现供应链完美协调,必须选取适当的成本分担系数的值,使得供应链成员的期望利润不小于保留值。例如,当保留值为批发价契约(
)下的期望利润时,取
,则有
,
,此时,供应链可以实现完美协调。
逐步减少,
和
逐步增加,即在协调的情况下,当成本分担系数增加时,损失系数和单位回购价也增加,零售商期望效用和期望利润逐步减少,而供应商的期望效用和期望利润则逐步增加。因此,要实现供应链完美协调,必须选取适当的成本分担系数的值,使得供应链成员的期望利润不小于保留值。例如,当保留值为批发价契约(
)下的期望利润时,取
,则有
,
,此时,供应链可以实现完美协调。
其次,考察风险厌恶程度对联合契约参数取值的影响。在
且
在
取值,
在
取值且
和
,
均在在
取值的三种情况下,分别计算满足命题6条件的成本分担系数
的取值范围,结果如表2。由表2可知:在
或
取值不变、另一个变化的情况下,随着风险厌恶系数不断增大,成本分担系数
取值范围也不断扩大;但是,当在
和
的取值逐步变大时,成本分担系数
取值范围先是逐步变大然后逐步变小。这说明供应链成员的风险厌恶程度对协调契约的参数取值是有影响的。

Table 2. Impact of risk aversion coefficient on contract parameters
表2. 风险厌恶系数对契约参数的影响
6. 小结
本文研究了生产和需求不确定环境下零售商和供应商均是风险厌恶的供应链协调问题。理论分析表明:适当选择契约参数,回购–成本损失分担契约可以实现供应链协调。通过数值分析发现:在协调时,随着成本分担系数增加,损失系数和单位回购价也增加,零售商期望效用和期望利润逐步减少,而供应商的期望效用和期望利润则逐步增加,并且供应链成员的风险厌恶程度影响契约参数的取值。本文的研究工作丰富了供应链的协调理论,对零售商和供应商同时是风险厌恶的供应链管理决策具有一定的指导意义。
NOTES
*通讯作者。