二元(p, q)-Bernstein算子的逼近性质

doi:10.12677/AAM.2020.92028

期刊菜单

二元(p, q)-Bernstein算子的逼近性质
Approximation Properties of Bivariate (p, q)-Bernstein Operators

DOI: 10.12677/AAM.2020.92028, PDF, HTML, XML, 科研立项经费支持
作者: 高盼, 刘辉辉, 冷献祥：巢湖学院数学与统计学院，安徽合肥
关键词: 二元(p； q)-Bernstein算子；收敛速度；Lipschitz函数；Bivariate (p； q)-Bernstein Operators； Rate of Convergence； Lipschitz Function

摘要: 本文在(p, q)-Bernstein算子的基础上构建二元(p, q)-Bernstein算子，证明该算子的逼近定理；应用Volkov定理验证了该算子的一致收敛性，并估计其收敛速度，此结论推广了一元(p, q)-Bernstein算子的逼近结果。

Abstract: In this paper, we introduce the bivariate (p, q)-Bernstein operator on the basis of (p, q)-Bernstein operator, and obtain the approximation theorem of the operator. The uniform convergence of the operator is verified by applying Volkov theorem, and its convergence rate is estimated. Those re-sults further promote some of the conclusions of (p, q)-Bernstein operator.

文章引用：高盼, 刘辉辉, 冷献祥. 二元(p, q)-Bernstein算子的逼近性质[J]. 应用数学进展, 2020, 9(2): 244-250. https://doi.org/10.12677/AAM.2020.92028

1. 引言

算子是逼近理论重要的研究对象，其中经典的算子之一为Bernstein算子。最早于1912年，Bernstein首次提出。其后，众多研究者开始关注研究Bernstein算子的推广。于是，Bernstein算子的各种变形算子纷纷被讨论，如Szász-Mirakjan-Kantorovich算子 [1]，Baskakov算子 [2] 等。

随着数学与生产生活各领域的交错发展，学者们将q微积分引入逼近理论，构造出大量q型算子。2007年，Dalmanoglu Ö. [3] 研究了q-Bernstein-Kantorovich算子；2011年，Muraru C V [4] 提出q-Bernstein-Schurer算子，并研究其逼近问题；伴随着研究的进一步深化，二元或多元算子相继被提出，故得到了大量二元算子关于逼近的相关理论，详见文献 [5] [6] [7] 等。

q微积分在逼近中的发展推动了(p, q)微分学步入逼近理论。Mursaleen于2015年首次在q-Bernstein算子的基础上提出(p, q)-Bernstein算子 [8]，实现了q-Bernstein算子性质的推广。自此，有关于(p, q)型算子呈现于世人面前。2016年，Acar在文献 [9] 中构建了两元(p, q)-Bernstein-Kantorovich算子并证明该算子一些的逼近结论。由此可知，关于(p, q)型二元算子逼近问题的研究正在持续发展中。本文构建出二元(p, q)Bernstein算子，证明算子的一些逼近相关的定理，从而更进一步推广一元算子的逼近性质，更加丰富逼近理论的完整性。

2. 知识储备

下文中出现的符号： ${[n]}_{p, q}, {[n]}_{p, q}!, {[\begin{array}{l} n \\ k \end{array}]}_{p, q}$ 主要定义为：

${[n]}_{p, q} = \frac{p^{n} - q^{n}}{p - q}, n = 0, 1, 2, \dots$

${[n]}_{p, q}! = {\begin{cases} 1, n = 0; \\ {[n]}_{p, q} {[n - 1]}_{p, q} \dots [1], n = 1, 2, \dots \end{cases}$

${[\begin{array}{l} n \\ k \end{array}]}_{p, q} = \frac{{[n]}_{p, q}!}{{[k]}_{p, q}! {[n - k]}_{p, q}!}$

定义1 [8] ：设 $f \in C [0, 1]$ ， $0 < q < p \leq 1$ ， $\forall x \in [0, 1]$ ，则(p, q)-Bernstein算子定义为下式：

$B_{n}^{p, q} (f; x) = \sum_{k = 0}^{n} b_{n, k}^{p, q} (x) f (\frac{p^{n - k} {[k]}_{p, q}}{{[n]}_{p, q}}),$

其中 $b_{n, k}^{p, q} (x) = {[\begin{array}{l} n \\ k \end{array}]}_{p, q} p^{[k (k - 1) - n (n - 1)] / 2} x^{k} \prod_{s = 0}^{n - k - 1} (p^{s} - q^{s})$ 。

定义2：设 $0 < q < p \leq 1$ ， $f \in C [0, 1]$ ，定义二元(p, q)-Bernstein算子为：

$B_{n_{1} n_{2}} (f; x, y) = \frac{1}{p_{1}^{\frac{n_{1} (n_{1} - 1)}{2}}} \frac{1}{p_{2}^{\frac{n_{2} (n_{2} - 1)}{2}}} \sum_{k_{1} = 0}^{n_{1}} \sum_{k_{2} = 0}^{n_{2}} b_{n_{1} n_{2} k_{1} k_{2}} (x, y) (x, y) f (\frac{p_{1}^{n_{1} - k_{1}} {[k_{1}]}_{p_{1}, q_{1}}}{{[n_{1}]}_{p_{1}, q_{1}}}, \frac{p_{2}^{n_{2} - k_{2}} {[k_{2}]}_{p_{2}, q_{2}}}{{[n_{2}]}_{p_{2}, q_{2}}})$

其中

$b_{n_{1} n_{2} k_{1} k_{2}} (x, y) = {[\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} {[\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p_{1}^{\frac{k_{1} (k_{1} - 1)}{2}} p_{2}^{\frac{k_{2} (k_{2} - 1)}{2}} x^{k_{1}} y^{k_{2}} \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) .$

引理1 [8] ：设 $0 < q < p \leq 1$ ， $x \in [0, 1]$ ，则有

$\begin{array}{l} B_{n}^{p, q} (e_{0}; x) = 1, B_{n}^{p, q} (e_{1}; x) = x, \\ B_{n}^{p, q} (e_{2}; x) = \frac{p^{n - 1}}{{[n]}_{p, q}} x + \frac{q {[n - 1]}_{p, q}}{{[n]}_{p, q}} x^{2} . \end{array}$

引理2：设 $0 < q_{1} < p_{1} \leq 1, 0 < q_{2} < p_{2} \leq 1$ ， $e_{i j} : I^{2} \times I^{2}, e_{i j} (x, y) = x^{i} y^{j}, 0 \leq i + j \leq 2$ ， $I^{2} = [0, 1] \times [0, 1]$ ，( $i, j$ 为正整数)，则有下列等式成立：

$\begin{array}{l} B_{n_{1} n_{2}} (e_{00}; x, y) = e_{00} (x, y); \\ B_{_{n_{1} n_{2}}} (e_{10}; x, y) = e_{10} (x, y); \\ B_{n_{1} n_{2}} (e_{01}; x, y) = e_{01} (x, y); \\ B_{n_{1} n_{2}} (e_{11}; x, y) = e_{11} (x, y); \\ B_{n_{1} n_{2}} (e_{20}; x, y) = e_{20} (x, y) + \frac{p_{1}^{n_{1} - 1} x (1 - x)}{{[n_{1}]}_{p_{1}, q_{1}}}; \\ e_{n_{1} n_{2}} (e_{02}; x, y) = e_{02} (x, y) + \frac{p_{2}^{n_{2} - 1} y (1 - y)}{{[n_{2}]}_{p_{2}, q_{2}}} . \end{array}$

证明：根据算子定义式与引理1，计算可得

$\begin{array}{l} B_{n_{1}}_{n_{2}} (e_{00}; x, y) \\ = \frac{1}{p_{1}^{\frac{n_{1} (n_{1} - 1)}{2}}} \frac{1}{p^{\frac{n_{2} (n_{2} - 1)}{2}}} \sum_{k_{1} = 0}^{n_{1}} \sum_{k_{2} = 0}^{n_{2}} {[\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} {[\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p_{1}^{\frac{k_{1} (k_{1} - 1)}{2}} p_{2}^{\frac{k_{2} (k_{2} - 1)}{2}} x^{k_{1}} y^{k_{2}} \times \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) \\ = \frac{1}{p_{1}^{\frac{n_{1} (n_{1} - 1)}{2}}} \sum_{k_{1} = 0}^{n_{1}} {[\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} p^{\frac{k_{1} (k_{1} - 1)}{2}} x^{k_{1}} \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \times \frac{1}{p_{2}^{\frac{n_{2} (n_{2} - 1)}{2}}} {\sum_{k_{2} = 0}^{n_{2}} [\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p^{\frac{k_{2} (k_{2} - 1)}{2}} y^{k_{2}} \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) \\ = B_{n_{1}} (e_{0}; x) B_{n_{2}} (e_{0}; y) = e_{00} (x, y), \end{array}$

$\begin{array}{l} B_{n_{1}}_{n_{2}} (e_{10}; x, y) \\ = \frac{1}{p^{\frac{n_{1} (n_{1} - 1)}{2}}} \frac{1}{p^{\frac{n_{2} (n_{2} - 1)}{2}}} \sum_{k_{1} = 0}^{n_{1}} \sum_{k_{2} = 0}^{n_{2}} {[\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} {[\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p^{\frac{k_{1} (k_{1} - 1)}{2}} p^{\frac{k_{2} (k_{2} - 1)}{2}} x^{k_{1}} y^{k_{2}} \\ \times \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) \frac{{[k_{1}]}_{p_{1}, q_{1}}}{p_{1}^{k_{1} - n_{1}} {[n_{1}]}_{p_{1}, q_{1}}} \\ = \frac{1}{p^{\frac{n_{1} (n_{1} - 1)}{2}}} \frac{1}{p^{\frac{n_{2} (n_{2} - 1)}{2}}} \sum_{k_{1} = 0}^{n_{1}} {[\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} p_{1}^{\frac{k_{1} (k_{1} - 1)}{2}} x^{k_{1}} \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \frac{{[k_{1}]}_{p_{1}, q_{1}}}{p_{1}^{k_{1} - n_{1}} {[n_{1}]}_{p_{1}, q_{1}}} \\ \times {\sum_{k_{2} = 0}^{n_{2}} [\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p^{\frac{k_{2} (k_{2} - 1)}{2}} y^{k_{2}} \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) \\ = B_{n_{1}} (e_{1}; x) B_{n_{2}} (e_{0}, y) = e_{10} (x, y) \end{array}$

$\begin{array}{l} B_{n_{1}}_{n_{2}} (e_{11}; x, y) \\ = \frac{1}{p^{\frac{n_{1} (n_{1} - 1)}{2}}} \frac{1}{p^{\frac{n_{2} (n_{2} - 1)}{2}}} {\sum_{k_{1} = 0}^{n_{1}} \sum_{k_{2} = 0}^{n_{2}} [\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} {[\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p_{1}^{\frac{k_{1} (k_{1} - 1)}{2}} p_{2}^{\frac{k_{2} (k_{2} - 1)}{2}} x^{k_{1}} y^{k_{2}} \\ \times \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) \frac{{[k_{1}]}_{p_{1}, q_{1}}}{p_{1}^{k_{1} - n_{1}} {[n_{1}]}_{p_{1}, q_{1}}} \frac{{[k_{2}]}_{p_{2}, q_{2}}}{p_{2}^{k_{2} - n_{2}} {[n_{2}]}_{p_{2}, q_{2}}} \\ = \frac{1}{p_{1}^{\frac{n_{1} (n_{1} - 1)}{2}}} {\sum_{k_{1} = 0}^{n_{1}} [\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} p_{1}^{\frac{k_{1} (k_{1} - 1)}{2}} x^{k_{1}} \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \frac{{[k_{1}]}_{p_{1}, q_{1}}}{p_{1}^{k_{1} - n_{1}} {[n_{1}]}_{p_{1}, q_{1}}} \\ \times \frac{1}{p_{1}^{\frac{n_{2} (n_{2} - 1)}{2}}} \sum_{k_{2} = 0}^{n_{2}} {[\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p_{2}^{\frac{k_{2} (k_{2} - 1)}{2}} y^{k_{2}} \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) \frac{{[k_{2}]}_{p_{2}, q_{2}}}{p_{2}^{k_{2} - n_{2}} {[n_{2}]}_{p_{2}, q_{2}}} \\ = B_{n_{1}} (e_{1}, x) B_{n_{2}} (e_{1}, y) = e_{11} (x, y) \end{array}$

$\begin{array}{l} B_{n_{1}}_{n_{2}} (e_{02}; x, y) \\ = \frac{1}{p_{1}^{\frac{n_{1} (n_{1} - 1)}{2}}} \frac{1}{p_{2}^{\frac{n_{2} (n_{2} - 1)}{2}}} \sum_{k_{1} = 0}^{n_{1}} \sum_{k_{2} = 0}^{n_{2}} {[\begin{matrix} n_{1} \\ k_{1} \end{matrix}]}_{p_{1}, q_{1}} {[\begin{matrix} n_{2} \\ k_{2} \end{matrix}]}_{p_{2}, q_{2}} p_{1}^{\frac{k_{1} (k_{1} - 1)}{2}} p_{2}^{\frac{k_{2} (k_{2} - 1)}{2}} x^{k_{1}} y^{k_{2}} \\ \times \prod_{s = 0}^{n_{1} - k_{1} - 1} (p_{1}^{s} - q_{1}^{s} x) \prod_{s = 0}^{n_{2} - k_{2} - 1} (p_{2}^{s} - q_{2}^{s} y) \frac{{[k_{2}]}_{p_{2,} q_{2}}^{2}}{p_{2}^{2 k_{2} - 2 n_{2}} {[n_{2}]}_{p_{2}, q_{2}}^{2}} \\ = y^{2} + \frac{(q_{2} {[n_{2} - 1]}_{p_{2}, q_{2}} - {[n_{2}]}_{p_{2}, q_{2}}) y^{2} + p_{2}^{n_{2} - 1} y}{{[n_{2}]}_{p_{2}, q_{2}}} \\ = y^{2} + \frac{p_{2}^{n_{2} - 1} y (1 - y)}{{[n_{2}]}_{p_{2}, q_{2}}} = B_{n_{1}} (e_{0}, x) B_{n_{2}} (e_{2}, y) \\ = e_{02} (x, y) + \frac{p_{2}^{n_{2} - 1} y (1 - y)}{{[n_{2}]}_{p_{2}, q_{2}}} . \end{array}$

同理可证出 $B_{n_{1} n_{2}} (e_{01}; x, y) = e_{01} (x, y)$ ； $B_{n_{1}, n_{2}} (e_{20}, x, y) = e_{20} (x, y) + \frac{p_{1}^{n_{1} - 1} x (1 - x)}{{[n_{1}]}_{p_{1}, q_{1}}}$ ，故引理成立。

引理3：设 $0 < q_{1} < p_{1} \leq 1, 0 < q_{2} < p_{2} \leq 1$ ， $x \in [0, 1]$ ，则有下列等式成立：

$\begin{array}{l} B_{n_{1} n_{2}} (e_{10} - x; x, y) = 0; \\ B_{n_{1} n_{2}} (e_{01} - x; x, y) = 0; \\ B_{n_{1} n_{2}} ({(e_{10} - x)}^{2}; x, y) = \frac{p_{1}^{n_{1} - 1} x (1 - x)}{{[n_{1}]}_{p_{1}, q_{1}}}; \\ B_{n_{1} n_{2}} ({(e_{01} - x)}^{2}; x, y) = \frac{p_{2}^{n_{2} - 1} y (1 - y)}{{[n_{2}]}_{p_{2}, q_{2}}} . \end{array}$

证明：根据引理2与算子的线性性质易得结论。

3. 主要结果

首先介绍一些记号：设 $δ_{1} > 0, δ_{2} > 0$ ， $f \in C (I^{2})$ ， $I^{2} = [0, 1] \times [0, 1]$ ，则关于f的连续性模可以表示为：

$ω (f : δ_{1}, δ_{2}) = \sup {| f (t, s) - f (x, y) | : (t, s) (x, y) \in (I_{1} \times I_{2}), | t - x | \leq δ_{1}, | s - y | \leq δ_{2}}$ ；

并且 $ω (f : δ_{1}, δ_{2})$ 满足以下性质：

$\begin{array}{l} (i) ω (f : δ_{1}, δ_{2}) \to 0, 若 δ_{1}, δ_{2} \to 0 \\ (ii) f (t, s) - f (x, y) \leq ω (f : δ_{1}, δ_{2}) (1 + \frac{| t - x |}{δ_{1}}) (1 + \frac{| s - y |}{δ_{2}}) \end{array}$

$α_{1}, α_{2}$ 阶Lipschitz条件的二元函数f：对于 $\forall (t, s), (x, y) \in I^{2}$ ， $f \in C (I^{2})$ ， $0 < α_{1} \leq 1, 0 < α_{2} \leq 1$ ，则存在常数 $M > 0$ ，使得 $| f (t, s) - f (x, y) | \leq M {| t - x |}^{α_{1}} {| s - y |}^{α_{2}}$ ；记为 $f \in L i p_{M} (α_{1}, α_{2})$ 。

定理1：若 $p_{1} = p_{n_{1}}, p_{2} = p_{n_{2}}, q_{1} = q_{n_{1}}, q_{2} = q_{n_{2}}$ ，且 $q_{1} \in (0, 1), p_{1} \in (q_{1}, 1], q_{2} \in (0, 1), p_{2} \in (q_{2}, 1]$ ， $\lim_{n \to \infty} p_{n_{1}} = 1, \lim_{n \to \infty} p_{n_{2}} = 1, \lim_{n \to \infty} q_{n_{1}} = 1, \lim_{n \to \infty} q_{n_{2}} = 1$ ，则对于 $\forall f \in C (I^{2})$ ，都有 $\lim_{n_{1}, n_{2} \to \infty} ‖ B_{n_{1}, n_{2}} (f; x) - f (x) ‖ = 0$ 。

证明：根据引理2得到

$\begin{array}{l} ‖ B_{n_{1} n_{2}} (e_{00} : x, y) - e_{00} ‖ = 0; \\ ‖ B_{n_{1} n_{2}} (e_{10} : x, y) - e_{10} ‖ = 0; \\ ‖ B_{n_{1} n_{2}} (e_{01} : x, y) - e_{01} ‖ = 0; \end{array}$

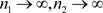又因为当时，

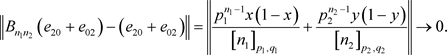
故根据Volkov定理的内容可以得到。

定理2：若，有不等式

其中。

证明：根据二元函数连续模的性质，则有

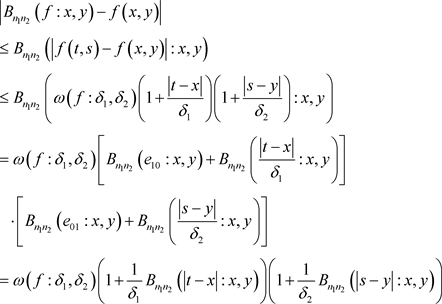
又利用Cauchy-Schwarz不等式与引理3，有

因此，得到

取，即成立。

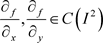定理3：设且，则有

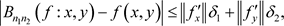
其中

证明：因为，可得

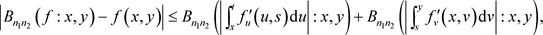
又因为

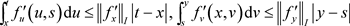
利用算子作用与柯西–施瓦茨不等式计算有

定理4：若，则存在一个常数，有下式成立：

其中。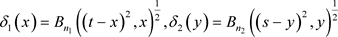

证明：由，计算可得

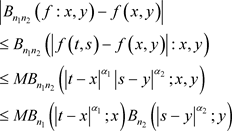
利用Hölder不等式，取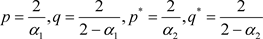

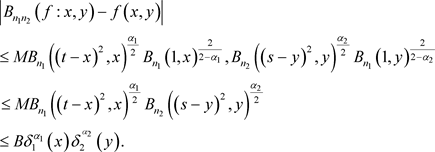
取即定理成立。

致谢

本文的写作感谢查星星老师的指导。

基金项目

巢湖学院国家级大学生创新创业训练计划资助项目(201910380035)，巢湖学院省级大学生创新创业训练计划资助项目(S201910380068)。

参考文献

[1]	Totik, V. (1983) Approximation by Szász-Mirakjan-Kantorovich Operators in Lp (p > 1). Analysis Mathematica, 9, 147-167. https://doi.org/10.1007/BF01982010
[2]	Pethe, S. (1984) On the Baskakov Operator. Indian Journal of Mathematics, 26, 43-48.
[3]	Dalmanoglu, Ö. (2007) Approximation by Kantorovich Type q-Bernstein Operators. Proceedings of the 12th WSEAS International Conference on Applied Mathematics, Cairo, Egypt, 29-31 December 2007, 113-117.
[4]	Muraru, C.V. (2011) Note on q-Bernstein-Schurer Operators. Studia Universitatis Babes-Bolyai Mathematica, 56, 489-495.
[5]	Simeonov, P. and Zafiris, V. (2008) Geometric Applications of Bivariate q-Bernstein and q-Orthogonal Polynomials. American Conference on Applied Mathematics, 3, 25-28.
[6]	Agrawal, P.N., Finta, Z. and Kumar, A.S. (2015) Bivariate q-Bernstein-Schurer-Kantorovich Operators. Results in Mathematics, 67, 365-380. https://doi.org/10.1007/s00025-014-0417-z
[7]	Pop, O.T. and Fărcaş, M.D. (2009) About the Bivariate Operators of Durrmeyer-Type. Demonstratio Mathematica, 42, 97-107. https://doi.org/10.1515/dema-2009-0110
[8]	Mursaleen, M., Ansari. K.J. and Khan, A. (2016) Erratum to “On (p, q)-Analogue of Bernstein Operators [Appl. Math. Comput. 266 (2015) 874-882]. Applied Mathematics and Computation, 278, 70-71. https://doi.org/10.1016/j.amc.2016.02.008
[9]	Acar, T., Aral, A. and Mohiuddine, S.A. (2016) Approximation by Bivariate (p, q)-Bernstein-Kantorovich Operators. Iranian Journal of Science and Technology, Transactions A: Science, 42, 655-662. https://doi.org/10.1007/s40995-016-0045-4

为你推荐

友情链接