基于模糊评价矩阵的新高考选科推荐系统

New College Entrance Examination Selection Recommendation System Based on Fuzzy Evaluation Matrix

摘要: 伴随着新高考改革的进展，考生如何选择最适合自身的科目迫在眉睫。本文针对以考生个性化选择为推荐重点，将模糊综合评价法运用于高考选科推荐中，运用协同过滤算法加快高考选科推荐系统的运行，利用会话式交互决策根据职业愿景与大学专业推荐选科。本文设计了一个完整的系统，在系统中将上述的方法运用其中，从而达到比单一成绩因素选科更好的效果。最后，通过在某中学的调查实验，构造模糊矩阵，确定出前5个影响选科的因素，即成绩、兴趣、职业倾向、家庭意愿、学生特质的影响权重，进行选科推荐，达到显著的效果，从而更好的满足考生的多方面需求。

Abstract: With the progress of the new college entrance examination reform, it is urgent for candidates to choose the most suitable subjects for themselves. This paper focuses on the personalized selection of candidates, applies the fuzzy comprehensive evaluation method to the recommendation of the college entrance examination, uses the cooperative filtering algorithm to speed up the operation of the recommendation system of the college entrance examination, and uses the conversational interactive decision-making to recommend the subject selection according to the career vision and the university specialty. This paper designs a complete system, in which the above methods are applied in the system, so as to achieve better results than a single score selection. Finally, the fuzzy matrix is constructed through the investigation experiment in a middle school, and the first five factors affecting the subject selection are identified. Performance, interest, professional tendency, the family will, the influence weight of student’s characteristics, carry on the selection section recommendation, achieve the remarkable effect, thus better satisfy the examinee’s many aspects demand.

1. 引言

随着新高考改革的不断深化，河北、辽宁、江苏、福建、湖北、湖南、广东、重庆八个省市于2018年首次采用3 + 1 + 2的新高考模式。考生的数学、语文、外语三科必选，在物理、历史之间选择其一，再从化学、生物、地理、政治任选其二即可。在此前提下，考生应该如何科学合理的选科已成为当务之急。而国内目前只有上海、浙江、山东三个省市开展了新高考改革，并且采取的是不同于上述所说新高考模式，即3 + 3 (4)新高考模式。其新高考模式已经呈现出诸多弊端，因此，在新高考改革前提下研究利用新的技术与算法对考生进行选科推荐与指导，为考生提供一种新的选科途径是十分必要的。

目前，在教育领域，模糊综合评价法的应用相当广泛。文献 [1]，基于Vague集的模糊综合评价法，避免了以往评分函数容易造成的结果与直觉不相符问题，使得评价结果更符合参评专家的直觉判断。但又在高考选科中的使用效果不佳。文献 [2] 运用结合变换原理与最大隶属度原则的动态模糊综合评价法，在大数据背景下根据各项因素的指标特征值构建判断矩阵。文献 [3] 将信息化学习满意度指标体系划分为：学习意识、学习行为、学习效果、课堂应用和学习条件，5大方面。在此基础上，构建出评价问卷进行实际测验。针对高考选科，本文将其归因于一类。文献 [4] 确定专家权威程度、专家意见的集中程度和专家意见的协调系数，进一步量化专家评测。传统的选科推荐只使用考生的成绩作为唯一变量进行选科推荐，学生也仅根据自己的兴趣或学习成绩决定选科，因此出现了在一学期后学生又希望重新选科的现象出现，对学生本身和教学资源来说都造成了不好的影响。故采用模糊综合评价法客观的推荐考生高考选科具有相当大的实用性和挑战性。

本文从多个可能影响学生选科及可能对学生未来成绩的造成影响的因素出发，在尊重考生个性化的基础上，将有可能影响考生选科的所有因素都列出并进行试验，得出考生所认为的最影响其选科的Top 5影响因素作为研究的起始点。基于此，采用模糊综合评价法进行研究，给出基于成绩以外的个性化推荐，以求满足考生的主观与客观条件，并推荐相关大学的相关专业。本文针对新高考条件下学科的全过程进行了深入研究，主要使用了模糊综合评价法进行选科决策，使用协同过滤算法加快推荐的速率和准确度，使用会话式决策进行选科与大学专业推荐。最后根据调查得到的数据，以一名考生为例，进行模糊综合评价法的推演，对比以往选科策略，得到了较为理想的结果。因此，可以为以后的新高考选科提供一条新的思路。

2. 理论与方法

2.1. 模糊综合评价法

模糊综合评价法是运用模糊矩阵，对一个受到多因素影响制约的事物或对象进行综合全面评价的评价方法 [5]。

2.1.1. 模糊综合评价模型的基本步骤

第一步，建立评价因素集 $U=\left\{u_1,u_2,\cdots ,u_n\right\}$，其中 $u_1,u_2,\cdots ,u_n$ 为能够影响到评价对象的n种因素。

第二步，建立评价集V，用 $V=\left\{v_1,v_2,\cdots ,v_m\right\}$ 表示。评价集存放的是评价者对被评价的对象做出的所有可能的评价结果 [6]。

第三步，建立权重集A，用 $A=\left\{a_1,a_2,\cdots ,a_n\right\}$ 来表示。由于各种因素在评价的过程中所起的作用不同，地位也不一样，因此就可以用权重数来表示各个因素的重要程度。基于所有影响因素从评价集中得出一个最优的评价结果就是模糊综合评价的目的 [7]。而权重集就是由所有的权数一起组成的集合。

第四步，进行单因素评判，并由单因素评判构造综合评判矩阵R。

第五步，综合评价。模糊综合评价的模型为：

$B=A\cdot R=\left(a_1,a_2,\cdots ,a_n\right)\left[\begin{array}{ccc}{r}_{11}& \cdots & r_{1m}\\ ⋮& \ddots & ⋮\\ r_{n1}& \cdots & r_{nm}\end{array}\right]=\left(b_1,b_2,\cdots ,b_m\right)$ (1)

其中b_j是由A与R的第j列运算得到的，表示被评级对象从整体上看对V_j等级模糊子集的隶属程度 [8]。

2.1.2. 确定评价指标体系

根据社会人口统计学信息，学生的特征由学生特点、学校环境以及家庭环境组成的。性格特质、思考方式、目标兴趣都不同的学生会做出不同的决定，通过学生在校期间的考试成绩来描述学生学校环境方面的特征，并要求学生根据自己的喜好对六门待选课程进行排名。此外，学生的决定往往会参考家长意见。因此可认为以上内容会对学生的选科决策造成影响，选取学生特质、平时成绩、学科喜好、职业倾向、父母意见为影响因子，分析五个因子的重要程度，最后得出因子对决策影响力的重要排序。建模如图1。

Figure 1. Fuzzy selection evaluation matrix model

图1. 模糊选科评价矩阵模型

按分析得到五个因子的权重 $A=\left\{a_1,a_2,\cdots ,a_n\right\}$，其中 $a_1+a_2+\cdots +a_n=1$。其中因子公式：

$a_j=\frac{c_j}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{c}_i}}$ (2)

2.2. 基于用户的协同过滤算法

基于用户的协同过滤算法主要考虑的是用户和用户之间的相似度 [9]。如图2所示，已知用户1喜欢某物品，而用户1与用户2是高度相似的，我们就可以预测用户2也是喜欢这个项目的，即可将此项目推荐给用户2。

Figure 2. User-based collaborative filtering algorithm

图2. 基于用户的协同过滤算法

其中，所使用的度量距离被称作余弦相似度。

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小 [10]。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫“余弦相似性” [11]。

$\cos \theta =\frac{{\displaystyle {\sum }_{i=1}^n\left(A_i\times B_i\right)}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(A_i\right)}^2}}\times \sqrt{{\displaystyle {\sum }_{i=1}^n{\left(B_i\right)}^2}}}$ (3)

基于在某学科组合具有较好学习能力的大部分学生应该有近似的性格特质这一思想，同样选科组合的调查问卷的问卷结果应有相似性。因此本文根据学生的推理能力、思考方式、逻辑思维能力、社交能力、记忆能力等方面准备一份心理测试问卷，并收集已进行过选科正处于高二并在自己所在的学科组合有较好成绩的学生的调查问卷。

我们记录收集学生的调查问卷结果，当某题的某选项被超过百分之五十的学生选择了，我们认为此选项为适合该选科组合的学生的特征之一。若有某题没有合适的特征，该题作为无效数据被舍弃。

最后每个选科组合都应有属于自己的特征向量 $X_1=\left[x_1,x_2,\cdots ,x_n\right]$，其中x_i的值为第1个选科组合在第i题的特征，例如正确标1，错误标0，无效标2。

当有新的需要被推荐选科的学生即目标用户，在做过调查问卷后生成属于自己的问卷结果向量，并使用余弦相似度算法与12个组合的特征向量进行匹配，最接近1的为最相似的用户特征，因此认为应把此特征向量的选科组合推荐给目标用户。

以上为根据学生特质进行选科推荐，具体见图3。

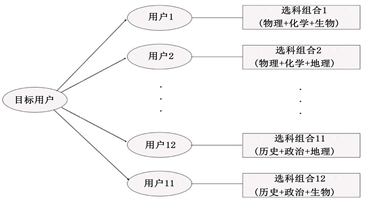
Figure 3. Subject selection model based on CF

图3. 基于协同过滤算法的选科模型

2.3. 会话式根据职业倾向进行选科决策

在求解问题的过程中，需要决策者和决策分析者不断的对话，持续参与决策过程，在决策者和参与者的相互作用中，逐步获得决策者的偏好结构，最后得到满意的决策结果。

会话式决策方法的一般步骤如下：

第一步，明确决策问题，将问题用数学模型描述。

第二步，对现有决策问题，求出一个决策者比较偏好的可行的非劣解。

第三步，与决策者交换信息，征求决策者对当前解的意见。

第四步，如果决策者很满意当前解或决策过程的终止判断被满足，当前解即为现有决策问题的最佳调和解，决策过程结束。否则，按下述步骤继续进行。

第五步，根据决策者的意见，修改决策方法，求出在相应偏好下新的比较偏好的非劣解，返回第三步 [8]。

本文将在根据职业倾向选择选科组合中应用会话式决策。

首先，导入用户信息进行初始化，进入社会行业选项，用户需在教育/IT/金融等社会行业中选择最感兴趣的行业。系统推荐一批与所选行业相关的职业，如果用户对此刻推荐的所有职业都不满意，则返回，重新选择社会行业，直至用户选择一个满意的职业。

根据所选择的职业，推荐一批相关的大学专业以供用户选择。若用户对推荐的大学专业均不感兴趣，则返回上一步，重新选择职业。

在选择大学专业后，系统会根据专业入学需求等信息，输出报考专业所必须选择的科目和建议选修的科目。

在完成整个流程后，根据每个人所选择的内容，进行系统优化，方便下一个用户的选择。流程图如图4。

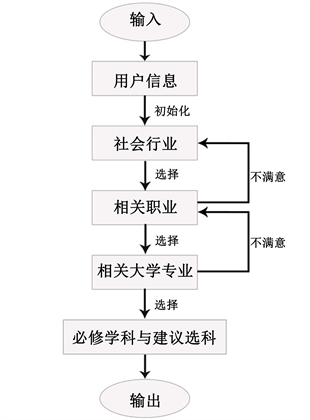
Figure 4. Conversational course selection decision flow chart

图4. 会话式选科决策流程图

2.4. 其他部分模型

在以学生成绩为指标时，记录该学生在校期间每次的月考、期中考试以及期末考试的在校排名，计算每科每次排名的平均值，物理历史中取平均排名更高一科，其余三科取其中最高的两科，被选科目在模糊矩阵中标1，其余学科标0。

以学生兴趣为指标时，我们需要学生按自己兴趣对六门待选学科进行排序。取学生排序的前三位学科，在模糊矩阵中标1，其余学科标0。

以父母意见为指标时，按照父母选出的三个学科进行标记。

3. 实验

3.1. 数据集

实验数据集为某中学已进行过选科的现高二学生的高一考试成绩排名以及调查问卷结果。调查问卷内容包括为考察推理能力、思考方式、逻辑思维能力等方面的题目，认为影响选科的因素的百分比，学科喜好排序，以及理想职业 [12] - [17]。

3.1.1. 确定指标权重

在我们的调查问卷中，就影响选科的因素列出常见的10种因素，测试人数为1000人，测试人群对象为已进行过选科的学生，根据随机抽样原则，确定出分数、兴趣、职业倾向、家庭意愿、学生特质为前5种影响因素向量{c_i}，占比分别为99.2%、83.6%、59.5%、35.2%、24.3%。带入公式(2)，得到的权重为0.33、0.28、0.2、0.11、0.08。即 $A=\left[0.33,0.28,0.2,0.11,0.08\right]$。

3.1.2. 选科组合特征

调查问卷包括二十二题，具体取值如下表1。

Table 1. Explanation and description of the questionnaire

表1. 调查问卷解释描述

抽取其中每个选科组合中校排名前一百名学生的调查问卷，确定每个选科组合的特征向量。由于目前仅有一届学生参与过选科，因此并未收集到所有选科组合的特征。已收集到的选科组合特征向量见表2。

Table 2. Feature vector of each subject combination

表2. 各选科组合特征

3.2. 进行模糊综合评价选科

现以一中学某学生X_x数据为例，阐述模糊综合评价在新高考选科推荐中的应用。由调查问卷结果判断学生受学生特质、平时成绩、学科喜好、职业倾向、父母意见五个指标的影响，即设 $U=\left\{u_1,u_2,\cdots ,u_5\right\}$ = {学生特质，平时成绩，学科喜好，职业倾向，父母意见}表示五种指标的因素值。

设向量 $V=\left\{V_1,V_2,\cdots ,V_6\right\}$ = {物理，化学，生物，历史，政治，地理}来表示评价集，即当只考虑一个指标的时候应选择的学科都有哪些。根据选科的影响因素每个学生均存在五个评价集，v_i是依据权重排列顺序的第i个因素的评价向量。在矩阵V中，v_ij表示在考虑等i个指标时j学科是否被选，被选学科应标1，未选学科标0。

而后建立均衡平均型评价矩阵 $R=\left[\begin{array}{ccc}{r}_{11}& \cdots & r_{16}\\ ⋮& \ddots & ⋮\\ r_{51}& \cdots & r_{56}\end{array}\right]$，其中

$r_{ij}=\frac{v_{ij}}{{\displaystyle {\sum }_{j=1}^6{v}_{ij}}}$ (4)

由此可得出综合评价结果 $B=A\cdot R=\left(b_1,b_2,\cdots ,b_6\right)$。

b_j为j学科最后的综合评分，也是隶属最后选科组合的程度，取其中综合最高的三个学科为最后的决策学科。

综合高一阶段的六次考试成绩，该生校平均排名见表3。

Table 3. The average school ranking of Student Xx

表3. 学生X_x的考试平均排名

因此在只考虑成绩时，物理历史中选择物理，其余科目中选择化学地理，最后推荐该生选择“物化地”组合。因此该生的 $v_1=\left[1,1,0,0,0,1\right]$。

问卷要求该生对六门待选学科进行排名，该生排序结果：物理>化学>生物>地理>政治>历史。即 $v_2=\left[1,1,1,0,0,0\right]$。

由于所有数据均由问卷得到，职业倾向和父母建议也是学生直接填写的。学生X_x填写的理想职业为医生，父母意见为“物化地”。根据专业入学需求，医生相关专业要求必选物理，根据大学专业课程建议选择生物。因此 $v_3=\left[1,0,1,0,0,0\right]$， $v_4=\left[1,1,0,0,0,1\right]$。

根据学生X_x的问卷结果得到特征 $X_x=\left[2,1,1,1,1,1,0,0,1,1,1,0,0,1,1,0,1,0,1,1,1,1\right]$，将该目标向量与各选科组合向量分别代入余弦相似度公式，得到结果最接近1的为

$\cos \theta \left(X_x,X_3\right)=\frac{{\displaystyle {\sum }_{i=1}^n\left(X_x{}_i\times X_3{}_i\right)}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(X_x{}_i\right)}^2}}\times \sqrt{{\displaystyle {\sum }_{i=1}^n{\left(X_3{}_i\right)}^2}}}$ = 0.78

即该生与“物理+化学政治”组合的特征更为相似，因此在只考虑学生特质时，根据协同过滤算法，认为该生选择“物化政”组合时有更大概率获得优异成绩。 $v_5=\left[1,1,0,0,1,0\right]$。

综上， $V=\left[\begin{array}{cc}\begin{array}{ccc}1& 1& 0\\ 1& 1& 1\\ 1& 0& 1\end{array}& \begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}1& 1& 0\\ 1& 1& 0\end{array}& \begin{array}{ccc}0& 0& 1\\ 0& 1& 0\end{array}\end{array}\right]$

代入公式(4)， $R=\left[\begin{array}{cccccc}1/3& 1/3& 0& 0& 0& 1/3\\ 1/3& 1/3& 1/3& 0& 0& 0\\ 1/2& 0& 1/2& 0& 0& 0\\ 1/3& 1/3& 0& 0& 0& 1/3\\ 1/3& 1/3& 0& 0& 1/3& 0\end{array}\right]$

根据公式(1)，进行模糊变换，便可得到模糊综合评价结果。

$\begin{array}{c}B=\left[0.33,0.28,0.2,0.11,0.08\right]\left[\begin{array}{cccccc}1/3& 1/3& 0& 0& 0& 1/3\\ 1/3& 1/3& 1/3& 0& 0& 0\\ 1/2& 0& 1/2& 0& 0& 0\\ 1/3& 1/3& 0& 0& 0& 1/3\\ 1/3& 1/3& 0& 0& 1/3& 0\end{array}\right]\\ =\left[0.367,0.267,0.193,0,0.03,0.147\right]\end{array}$

综合以上分析所得，推荐学生X_x选择“物理+化学生物”组合。

3.3. 实验结果与分析

3.3.1 评价指标

距离现高二的学生进行选科已过一年，根据某中学学生的自主选科结果和利用本文方法得到的选科结果采用准确路进行评价。下面通过混合矩阵介绍这两种评价指标，如表4。

Table 4. The mixed matrix

表4. 混合矩阵示意

根据上述混合矩阵，准确率的计算方式如下：

$A=\left(\text{TP}+\text{TN}\right)/\text{All}$ (5)

3.3.2. 实验结果

为说明模糊综合评价法对选科准确率的提升，本文与其他方法进行了对比实验，实验结果如表5。

Table 5. The result of comparing

表5. 对比实验结果

3.3.3. 实验分析

从实验结果来看，本文方法在准确率上有较好的表现。因此认为此模型可有效降低后悔学生的比例。

4. 总结

高中学生的选科关乎高考，应当谨慎准确的进行选择，因此应当从多方面综合考量。由于在考量的过程中受到多种因素的制约，并且这些影响因素具有模糊性和不确定性，因而我们应用模糊综合评价法，由定性评价转化为定量评价，通过对量化的指标进行打分评价得出综合评价结果进而进行准确的推荐。

本文将协同过滤算法和会话式决策与模糊矩阵相结合，通过建立模糊综合评价模型对高中学生适合的选科组合进行研究，并具体研究了模糊综合评价模型在新高考选科方面的应用。该方法为学生的选科提出了新的思路，能够很好地解决传统的评价方法考虑方面过于单一的问题。同时本文以一名学生为例，详细解释了如何使用该方法得到一个推荐结果，保证了该方法的科学性和可实施性。

本文的推荐结果对于高一学生的选科有很好的参考价值，对于降低后期后悔学生的比例具有重大意义。不足之处在于由于新高考制度刚刚开始应用，我们没有足够的数据集，因此在权重的设置方面以及以调查问卷为结果的科目组合特征均有一些偏差。我们在接下来的过程中会根据更多学生的数据来不断地完善模型，建立更加健全的推荐体系。

基金项目

这项工作得到河北省教育厅人文社会科学研究项目(招生考试专项)2018年度基金项目(编号：KSZX201802)，河北省引进留学人员资助项目C201816，河北省自然科学基金项目资助项目(F2019205303)，河北师范大学科技基金项目(L2019Z10)。

NOTES

^*通讯作者。