1. 引言
假设X是一个实随机变量,那么它的矩函数就是
的乘方的期望 [1] [2]。X的矩函数可表示样本分布的均值、离散程度和斜度等样本统计特性。矩函数在统计中有重要的地位,如利用矩函数可以实现统计模型中的参数估计 [3]。
矩生成函数可用于快速求解随机变量的各阶矩。利用矩生成函数,我们还可以研究不同阶矩之间的关系 [4] [5]。进一步,矩生成函数与一个变量的分布构成1-1对应关系。因此,我们可以通过矩生成函数来刻画一个随机变量的概率分布特性。另外,矩生成函数和累积生成函数都可以用于估计多元响应降维子空间 [6] [7]。而且,多元矩生成函数可以应用于射线照相胶片系统中信号和噪声传播分析 [8]。本文主要研究多元随机向量的矩生成函数及其应用。我们还将研究矩生成函数和累积生成函数之间的关系,以及它们在正态分布和γ分布中的应用。
2. 预备知识
定义2.1 实随机变量X的矩生成函数定义为随机变量
的期望,即
,t为实变量。若
为随机变量X的k阶矩(或记k-矩)。则矩生成函数满足
(2.1)
一个随机向量
的矩生成函数定义为
(2.2)
为实向量。进一步,随机矩阵
的生成函数定义为
(2.3)
其中
为实矩阵。
为矩阵U和X的内积。注意到(2.2)为(2.3)的特殊情形。
定义2.2 变量(包括向量与矩阵) X的累积生成函数定义为
(2.4)
对
进行幂级数展开:
(2.5)
定义
是Y的累积量。
一个随机张量
为一个多元随机数组,它为随机矩阵的高阶情形,其中m称
为A的阶。我们称
为A的大小。当
时,A称为m阶n维张量。所有第m阶n维实张量构成的集合记为 。
。
设
为大小相同的两个张量,定义它们的内积为
。
的内积也记为AB。
3. 主要结果
记
为一个2维随机向量,
。则
若记随机向量x的均值向量和协方差矩阵分别为
和
,那么有
定理3.1 设
为随机向量。则其矩生成函数Mx满足以下条件:
1)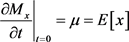 ;
;
2)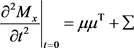 。
。
一个随机向量 的k阶矩共有nk个,它们构成一个k阶n维张量
的k阶矩共有nk个,它们构成一个k阶n维张量 ,定义为
,定义为
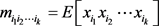 ,
,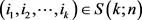 (3.1)
(3.1)
这里 。对
。对 ,记
,记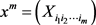 为由x生成的秩-1的m阶n维张量,其中
为由x生成的秩-1的m阶n维张量,其中 。下面的定理为本文主要结论之一:
。下面的定理为本文主要结论之一:
定理3.2 设随机变量 。则有
。则有
 (3.2)
(3.2)
证明:

我们由定理3.2,不难证明定理3.1。
定理3.3 设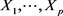 为独立随机变量,
为独立随机变量,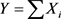 ,则Y的矩生成函数是Xi的矩生成函数之积,即:
,则Y的矩生成函数是Xi的矩生成函数之积,即:
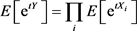 (3.3)
(3.3)
或
 (3.4)
(3.4)
证明:因为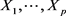 是独立的且
是独立的且 ,所以
,所以

为了说明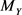 幂级数展开,我们先来考察Y的1-3阶矩。由Xi的独立性,有
幂级数展开,我们先来考察Y的1-3阶矩。由Xi的独立性,有
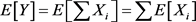 ,
,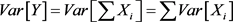
令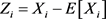 ,因
,因 彼此独立,所以
彼此独立,所以
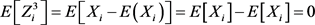
因此
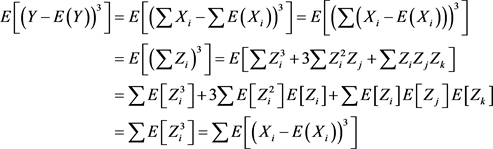
但是
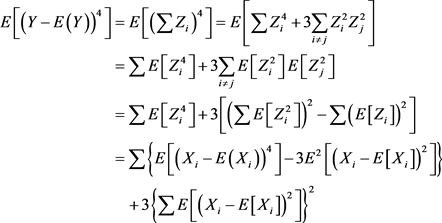
因此, 的幂级数展开不等于
的幂级数展开不等于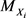 的幂级数展开之和。
的幂级数展开之和。
定理3.4 设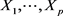 为独立随机变量,且
为独立随机变量,且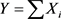 ,则
,则
 (3.5)
(3.5)
证明:(3.5)可由下式证得:
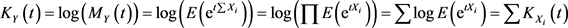
定理3.5 随机变量X的累积量满足以下条件:
 (3.6.1)
(3.6.1)
 (3.6.2)
(3.6.2)
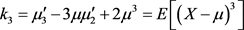 (3.6.3)
(3.6.3)
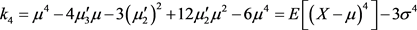 (3.6.4)
(3.6.4)

证明:由(3.3)式知
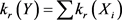 (3.7)
(3.7)
由式(2.1)和(2.4)得,X的累积生成函数可表为
 (3.8)
(3.8)
注意到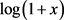 的幂级数展开
的幂级数展开
 (3.9)
(3.9)
取 ,则
,则
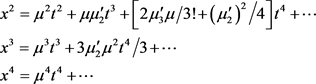 (3.10)
(3.10)
由(3.8~3.10)知
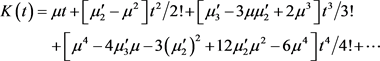 (3.11)
(3.11)
比较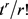 的系数,可得(3.6.1~3.6.4)。
的系数,可得(3.6.1~3.6.4)。
例3.1设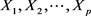 为随机变量且
为随机变量且 。则矩生成函数满足
。则矩生成函数满足
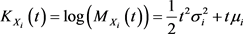 (3.12)
(3.12)
因此有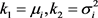 。若
。若 是独立随机变量,则
是独立随机变量,则 的累积生成函数为
的累积生成函数为
 (3.13)
(3.13)
它对应正态分布 。现考虑γ-分布
。现考虑γ-分布 ,则
,则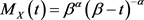 ,故累积生成函数为
,故累积生成函数为
 (3.14)
(3.14)
现设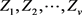 独立且服从标准正态分布,那么
独立且服从标准正态分布,那么 服从卡方分布。注意到
服从卡方分布。注意到
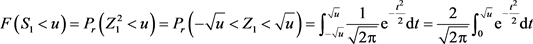
因此S1 (因此每个Si)的密度函数为 ,从而
,从而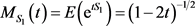 ,故
,故
 (3.15)
(3.15)
(3.15)为 的矩生成函数。因此
的矩生成函数。因此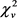 的密度函数和
的密度函数和 密度函数相同:
密度函数相同:
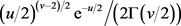
4. 张量矩生成函数和累积张量
随机向量的矩生成函数可以推广至随机张量的矩生成函数的情形:
定义4.1 一个随机张量 的矩生成函数定义为
的矩生成函数定义为
 (4.1)
(4.1)
其中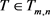 为任意m阶n维张量。
为任意m阶n维张量。
推论4.2 设 为随机张量。矩生成函数与矩函数之间满足关系:
为随机张量。矩生成函数与矩函数之间满足关系:
 (4.2)
(4.2)
其中 为
为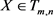 的矩函数。
的矩函数。
定理4.1 设 为统计独立随机张量,且
为统计独立随机张量,且 ,则
,则
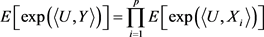 (4.3)
(4.3)
即Y的矩生成函数为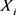 生成函数的积,或
生成函数的积,或
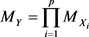 (4.4)
(4.4)
证明:因为 是线性无关的,且
是线性无关的,且 ,所以
,所以

定义4.2 张量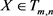 的累积张量为
的累积张量为
 (4.5)
(4.5)
定理4.2 Y的张量矩生成函数的对数是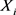 的张量矩生成函数的对数的总和。即
的张量矩生成函数的对数的总和。即
 (4.6)
(4.6)
证明:
同样,定义 是Y的累积量,则
是Y的累积量,则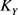 具有幂级数展开:
具有幂级数展开:
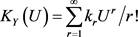 (4.7)
(4.7)
并且
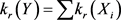 (4.8)
(4.8)
由公式(4.2)知,当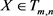 时,它的累积张量可以写为
时,它的累积张量可以写为
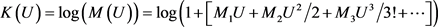 (4.9)
(4.9)
取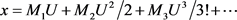 ,则
,则
 (4.10)
(4.10)
由公式(4.10)知,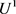 仅在x中出现,
仅在x中出现,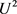 只出现在x和
只出现在x和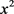 中,依此类推,我们可以得到
中,依此类推,我们可以得到
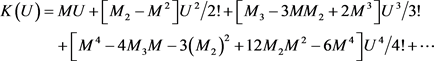 (4.11)
(4.11)
将累积量与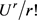 的系数进行比较,我们可以得到
的系数进行比较,我们可以得到
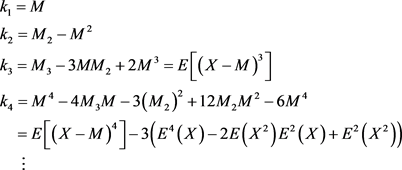 (4.12)
(4.12)