1. 容积法在缝洞型油藏储量计算中的应用局限
不同于均质性较好的常规砂岩油藏,缝洞型油藏以溶洞和裂缝为有效的储集空间,储层非均质性强,空间展布具有多尺度性,缝洞组合关系复杂。不能简单将缝洞型碳酸盐岩油藏视为连续介质,体现在三个方面:储集体在平面上的不连续和纵向上的差异性分布;裂缝、溶洞发育差别巨大且组合关系复杂;复杂的缝洞组合关系下流体流动通道条件的差异性。所以在缝洞型油藏中,不能用常规渗流方程描述。
计算地质储量,常规砂岩油藏通常采用容积法,而容积法适用于纵向上储层发育厚度一致的油藏,对于地质条件复杂、储集空间多尺度性强的缝洞型油藏,容积法具有一定的局限。缝洞型油藏的井网设计以及开发措施也不同于常规砂岩油藏,这使得在开发过程中缝洞型油藏的生产动态变化也更加复杂,对动态储量的计算变得困难 [1] [2] [3] [4]。
早在上个世纪,Ramey (1970)提出图版拟合的试井分析方法,Gringarten图版(1979)随后产生,数值模拟开始成为试井分析的重要手段。自Bourder (1983)提出压力导数的分析方法后,双对数曲线分析方法得到广泛应用并不断发展 [5] [6] [7]。本文将通过试井双对数曲线图版对储集体类型和规模进行识别。
2. 井–缝–单洞模型
2.1. 物理模型
碳酸盐岩缝洞型油藏的缝洞组合方式复杂,以“井–洞”、“井–缝–单洞”、“井–缝–双洞”、“井–洞–缝–洞”为主。本文以“井–缝–单洞”模型作为研究对象,如图1所示,油井钻遇地层,与裂缝直接相连,通过裂缝,与单溶洞沟通。溶洞作为流体主要储集空间和流动通道,裂缝作为流体主要流动通道。流体从溶洞流向裂缝,再经过裂缝流向井筒,溶洞不直接向井筒供液,流体在溶洞和裂缝中的流动均满足达西定律。另外,假设油井定产量生产,重力和毛细管力可忽略不计。
2.2. 数学模型
建立井–缝–单洞试井模型的数学微分方程组,对模型无因次化,并进行Laplace变换和Laplace空间求解,求得封闭外边界条件下Laplace空间中无因次井底压力解的表达式为:
 (1)
(1)
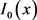 和
和 分别代表0阶和1阶的第1类虚变量贝塞尔函数,
分别代表0阶和1阶的第1类虚变量贝塞尔函数, 和
和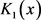 分别代表0阶和1阶的第2类虚变量贝塞尔函数,下标e代表边界,下标D代表各变量对应的无因次量,s——拉普拉斯空间变量,
分别代表0阶和1阶的第2类虚变量贝塞尔函数,下标e代表边界,下标D代表各变量对应的无因次量,s——拉普拉斯空间变量, ——井底压力,
——井底压力, ——边界半径。
——边界半径。
求实空间的数值解,本次采用Stehfest逆反演方法对表达式(1)中的Laplace空间中无因次井底压力 进行求解。针对任意函数
进行求解。针对任意函数 ,其Laplace变换公式为:
,其Laplace变换公式为:
 (2)
(2)
通过Stehfest数值反演, 表达式如下:
表达式如下:
 (3)
(3)
上式中,
 (4)
(4)
 (5)
(5)
表达式(5)中N值一般取正偶数,且当 时计算出的误差较小,精度较高。
时计算出的误差较小,精度较高。 时,
时,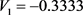 ,
, ,
, ,
, ,
, ,
, ,
, ,
,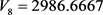 。
。
3. 试井双对数曲线溶洞容积影响图版
针对建立的物理模型、无因次数学模型,求得Laplace空间下的无因次压力解表达式,通过Stehfest数值反演得到数值反演表达式。借助计算机辅助软件Matlab进行编程,将两个表达式的代码输入,再输入恒定的参考值,得到井–缝–单洞模型封闭外边界下的试井双对数典型曲线图,如图2所示。
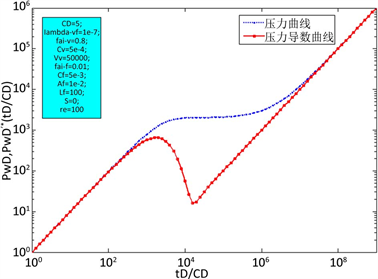
Figure 2. Typical log-log plot of well test
图2. 试井双对数典型曲线图
裂缝长度、溶洞容积大小、井储系数、表皮系数等都会影响压力曲线和压力导数曲线的形态特征 [8]。通过控制一系列参量为定值,调整溶洞容积VvD,可以得出受溶洞容积大小影响的不同形态的曲线,从而得到变溶洞容积参量的试井双对数曲线分析图版。从图3可以看出,封闭外边界条件下,当溶洞容积VvD增大,出现的下凹段深度越大,开度越宽,同时下凹段出现的时间变早。反映出溶洞越大,供液能力越强,单位时间内压降更小,压力保持程度更高。

Figure 3. Log-log plot of well test affected by vug volume VvD (closed outer boundary)
图3. 试井双对数曲线溶洞容积VvD影响图版(封闭外边界)
4. 计算缝洞型油藏储量
4.1. 计算步骤
将以上井–缝–单洞模型无因次溶洞容积VvD影响图版与实际井的试井双对数诊断图相结合比对,得到在实际井地下对应的溶洞容积大小,进而计算油藏动态储量,具体步骤如下。
第一步:通过钻井、测井、酸压资料以及地震解释资料等静态资料初步识别缝洞发育程度以及组合关系。
第二步:将实际井的试井曲线与无因次溶洞容积影响图版进行拟合。
第三步:通过曲线拟合得到吻合的溶洞容积,根据拟合点数据求出动态储量。
4.2. 实例计算
以塔河油田某单井为例。分析其钻井资料,钻井过程中无放空、漏失现象,判定该井未直接钻遇溶洞。分析过该井的连井地震剖面图,判断该井近井发育溶洞。后期该井进行酸压措施,根据酸压曲线显示对近井通道有一定的改善,酸压效果较好,沟通了一定规模储集体。初步分析该井连通模式可能为井–缝–单洞模式。
对该井进行压降试井作业,累计测试时间300小时左右。其原始双对数诊断曲线图如图4所示,分析认为通过酸蚀产生裂缝后,裂缝沟通了溶洞储集体,后期压力导数曲线上翘,反映为不渗透外边界。
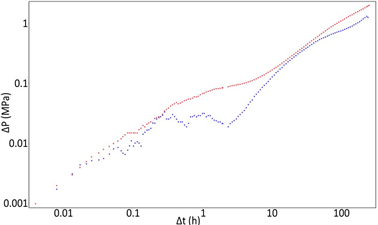
Figure 4. Log-log diagnostic plot of original falloff well test
图4. 原始压降试井双对数诊断图
综合该井的地质及生产特征,分析该井压降试井双对数诊断图形态特点,认为以井–缝–单洞模型对其解释较为合适。对该井进行图版拟合,将该井原始压降试井双对数曲线放置井–缝–单洞模型无因次溶洞容积VvD影响图版上,如图5所示。

Figure 5. Initial log-log plot of well test before matching
图5. 试井双对数曲线图版拟合前初始状态图
上下左右移动该井原始压降试井双对数曲线,使实测压力与压力导数数据对应于某个VvD值的压力及压导曲线拟合最好的状态。通过比对记录,此曲线的拟合值为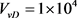 ,如图6所示。
,如图6所示。
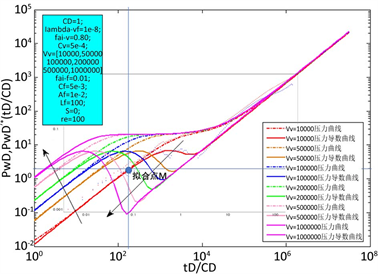
Figure 6. Effect log-log plot of well test after matching
图6. 试井双对数曲线图版拟合效果图
任取一个拟合点,如图6中蓝色圆点,其理论拟合点坐标为(190,1.95)M;对应实际数据的拟合点坐标为(0.09,0.009)M。下标M代表拟合点。
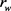 取值0.075 m,根据拟合点及无因次变量的定义,有:
取值0.075 m,根据拟合点及无因次变量的定义,有:

这样就得到了溶洞的有因次容积值,取含油饱和度 ,原油密度
,原油密度 ,原油体积系数
,原油体积系数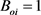 ,代入井–缝–单洞模型储量计算公式中有:
,代入井–缝–单洞模型储量计算公式中有:

5. 结论
1) 缝洞型油藏非均质性强,缝洞组合关系复杂,运用容积法计算其储量有一定局限性。
2) 试井双对数曲线形态受溶洞容积大小影响,曲线可反映油藏开发过程中地层能量随时间的动态变化特征。
3) 试井双对数曲线图版拟合可有效识别储集体类型和规模,并计算油藏动态储量。