1. 引言
设r是一个很大的整数,另设g是与r互质的整数且其模r的阶记为T。给定两个连续的整数区间
,
,其中
,
,我们定义二重指数和
,
其中
,
和
都是复数且
,
。
当r为素数p时,Boyrgain [1] 对于非常小的区间N和M估计了
关于此方面的内容也可以参考 [2]。最近,Shparlinski [3] 和Garaev [4] 分别得到了关于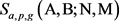 的新的估计。
的新的估计。
在本文中,我们主要给出
的边界,并由得到的结果给出同余方面的应用。文中会用到一些符号,例如
表示存在常数
使得
。另外,
表示
。
2. 主要结果
定理2.1:对于
,我们有
.
取
,则可推导出如下结果。
定理2.2:设
是一个很小的常数,
和
是连续的整数区间且其阶满足
,
,
那么对于任意整数
,同余方程
,
,
的解的个数
, 其中 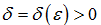 .
.
3. 引理
引理3.1:当
时,
;否则其值为0。
证明:当
时,求和号中每项均为1,因此和为r;
反过来,
。
证毕。
在Bourgain [5] 的定理1中取
,我们得到
引理3.2:设
是
的一个子群。如果
,那么对于任意正整数h,同余方程
,其中正整数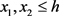 且
的解的个数
且
的解的个数
.
推论3.3:设
是
的一个子群。如果
,那么对于任意正整数h,同余方程
,其中正整数
且
的解的个数
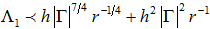 .
.
结合Garaev [4] 中的引理2,我们有
引理3.4:设
中
,
,那么同余方程
,
,
的解的个数
.
4. 定理2.1的证明
重新排列顺序并利用Cauchy-Schwarz不等式,我们有
.
因此,如果我们定义
为同余方程
,
的解的个数,那么
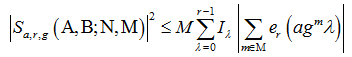 (1)
(1)
再次应用Cauchy-Schwarz不等式,我们得到
(2)
然而,因为 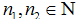 ,所以我们有
,所以我们有
(3)
另一方面,
.
由引理3.1,当 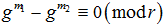 时,
;否则其值为0。
时,
;否则其值为0。
所以
. (4)
将(3)和(4)代入(2),得
.
再将其代入(1),我们便有
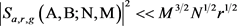 .
.
因此,定理2.1得证。
5. 定理2.2的证明
首先,我们将
改写为
. (5)
当
时,若
,则定理2.1证明中的(4)为
其中V为同余方程
,
的解的个数。
因此,
.
从而对于正整数a,我们恒有
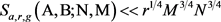 .
.
在(5)中,将
的项分离,并利用上述结果,我们有
(6)
其中
,
且
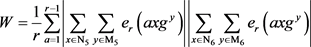 .
.
利用Cauchy-Schwarz不等式,我们得到
(7)
其中
是同余方程
 ,
,
,
,
的解的个数。
由引理3.4,我们有
, 其中
.
将其代入(7),得
, 其中
.
代入(6),我们有
, 其中
.
证毕。
致谢
感谢M. Z. Garaev的文章给我的思路,以及同事们对我工作的支持。