基于协同进化算法的支持向量回归径流建模研究与应用

Evolving Support Vector Regression by Co-Evolution Algorithm for Runoff Forecasting Modeling Research and Application

摘要: 针对支持向量回归模型在实际应用中难以选择建模数据的特征、核函数类型、最优核函数参数以及支持向量的惩罚系数和不敏感损失函数的参数问题，本文提出利用粒子群算法混合模拟退火算法构造协同进化算法，自适应选择建模数据的特征、协同进化选择支持向量回归的核函数类型，匹配最优核函数的参数和模型参数，以此建立协同进化的支持向量回归柳江径流预测模型。本文通过混合模拟退火算法Metropolis接受准则和粒子群算法随机接受准则，结合粒子群算法的并行计算和模拟退火算法的干扰机制，减少在局部搜索点附近的震动偏离构造协同进化算法，自适应筛选支持向量回归模型建模数据的特征、协同进化选择核函数类型，最优匹配核函数参数和支持向量模型参数，建立柳江径流建模，实验结果表明，该方法能够快速有效地选择建模数据的特征、核函数类型、最优匹配核函数参数和支持向量模型参数，其泛化性能明显提升，拟合效果更好。该方法用于柳江径流预测，具有良好的建模效果和更高的预测精度。

Abstract: Aiming at the difficulty of selecting the appropriate kernel function type, kernel function parame-ters, penalty coefficients of support vectors, and insensitive loss parameters in practical applica-tions of support vector model, in this paper, co-evolution algorithm is employed to simultaneously evolve selection the data features, the kernel type of support vector regression, the parameters of the kernel function and the model parameters, namely HPSOSA-SVR by hybrid the strengths of Particle Swarm Optimization (PSO) and Simulated Annealing (SA). In order to select the optimal support vector regression kernel function type, the optimal matching kernel function parameter and the support vector model parameter for runoff modelling, the co-evolution algorithm focuses on combining the advantages of PSO (fast calculation and easy mechanism) and SA (ability to jump away from local optimum solutions and converge to the global optimum solution) by combined the metropolis processes of SA into the movement mechanism and parallel processing of PSO. The HPSOSA algorithm has the capability of both fast calculation and searching in the direction of the global optimum solution, helping PSO jump out of local optima, avoiding into the local optimal solution early and leads to a good solution. Compared with HPSOSA, PSO and pure SVR, results show that the HPSOSA-SVR model can successfully identify the optimal type of kernel function and all the optimal values of the parameters of SVR with the lowest prediction error values in runoff forecasting, can significantly improve the runoff forecasting accuracy. Experimental results reveal that the predictions using the proposed approach are consistently better than those obtained using the other methods presented in this study in terms of the same measurements.

1. 引言

准确的径流预测建模是水文领域中一项具有十分挑战性的任务，也是减灾防灾的重要研究课题，精确可操作的径流预报模型对于水资源规划及综合开发利用，水利枢纽运行管理等重大决策问题的提供基本决策依据，对国民经济健康发展具有十分重要的意义。在水文科学研究中，虽然基于水文过程的径流物理模拟有了很大进展，但是由于降水径流过程的具有时空分布不均匀性和随机性、而且动力学模型的边界条件受地质和人类活动的因素影响太多 [1] [2] [3]，自然界中降水形成有效径流受降水、渗透、蒸发等气候因素影响很大，具有高度非线性、时变性、不确定性和强耦合等特性，对参数极端敏感等问题，使得径流过程的物理过程模型往往难以客观描述和构造，即使该模型可以构造，但是数学求解极为困难 [4] [5] [6]。而近年来随着计算机硬件和软件技术的发展，许多机器学习建模方法，如人工神经网络(Artificial Neural Network, ANN)、支持向量机(Support Vector Machine, SVM)方法迅速应用径流建模，它们不需要详细描述的径流物理过程，由于它具有很强的处理非线性问题的能力 [7] [8]，比一般的方法具有更好的预测能力，它为水文的径流建模分析提供了新技术、新方法 [9] [10]。

20世纪90年代由Vapnik等人提出的统计学习理论，在此基础上发展起来的支持向量机是一种新型机器学习方法。它是基于结构风险最小化原则，集成了最大间隔超平面、核技术、凸二次规划、稀疏解和松弛变量等多项技术 [11] [12]，在解决小样本、非线性及高维空间学习时显示了其卓越的优越性，被成功应用到函数拟合逼近，文本和手写识别等领域 [13] [14] [15] [16]。SVM在实际应用建模过程中，但是对于建模数据的特征选择、支持向量的核函数类型、核函数的参数以及支持向量的惩罚系数和不敏感损失函数参数没有理论指导，实际应用中采用交叉验证方法确定参数。这种方法虽然简单，但是过多地依赖设计者的经验，缺乏理论基础，得到的结果不稳定，这些问题影响SVM模型在实际应用中推广 [17] [18] [19] [20]。

本文利用粒子群–模拟退火算法构造协同进化计算技术，自适应选择建模数据的特征、协同进化支持向量机的核函数类型和匹配相关最优参数，以此建立广西柳江径流预测模型(Support Machine Regression with Hybrid Particle Swarm Optimization and Simulated Annealing, HPSOSA-SVR)。本文通过对广西柳江2008年，2009年和2010年汛期径流建立预测模型，计算结果表面该方法能够针对水文自身季节变化情况，选择建模数据的特征信息，协同进化最优核函数类型、匹配最优核函数和模型的参数，而且精度高、稳定性好，为径流建模预测分析提供了一种可靠、有效的途径和实际应用中可以操作的方法。

2. 混合进化支持向量回归建模

2.1. 支持向量机

支持向量机(Support Vector Machine, SVM)是在Vapnik等人提出的小样本统计学习理论基础发展而来的机器学习方法，其算法是基于VC 维数理论和结构风险最小化准则。在处理非线性问题时，通过非线性核函数将输入向量映射到高维线性特征空间，在这个空间构造样本最优超平面，以此将非线性问题就转化为高维空间中的线性问题，在模型的复杂性和泛化能力之间寻求最佳折中，并且能有效地克服维数灾和有效提高泛化能力 [17]。SVM按照使用的类别可以分为支持向量分类(Support Vector Classification, SVC)和支持向量回归(Support Vector Regression, SVR)，其中SVR算法用于时间序列的预测、非线性建模与预测、优化控制等方面。

对于给定的样本数据集合 $\left\{\left(x_i,y_i\right)|i=1,2,\cdots ,N\right\}$，其中 $x_i\in R^n$ 是输入数据， $y_i\in R$ 是输出数据，SVR方法是首先利用非线性映射 $\varnothing (\cdot )$ 将样本空间从原低维空间映射到高维特征空间，在高维特征空间进行线性回归估计输入和输出非线性关系，回归函数：

$f\left(x\right)={\omega }^{\text{T}}\phi \left(x\right)+b$ (1)

其中是 $\omega$ 权重向量， 是偏置量，将非线性估计函数转化为高维特征空间中的线性估计函数，利用结构风险最小化原理，引入不敏感损失函数的参数 $\epsilon$ 和松弛变量 $\xi ,{\xi }^{*}$，支持向量回归问题就转化为以下目标函数的最小化问题：

$\{\begin{array}{l}\min \left(\omega ,\xi ,{\xi }^{*}\right)=\frac{1}{2}{\omega }^{\text{T}}\omega +C{\displaystyle {\sum }_{i=1}^N\left(\xi +{\xi }^{*}\right)}\\ s.b.y_i-{\omega }^{\text{T}}\phi \left(x_i\right)-b\le \epsilon +\xi \\ -y_i+{\omega }^{\text{T}}\phi \left(x_i\right)+b\le \epsilon +{\xi }^{*}\\ \xi ,{\xi }^{*}\ge 0,i=1,2,\cdots ,N\end{array}$ (2)

其中C为惩罚参数，对其进行拉格朗日乘法求解二次规划得到回归函数：

$f\left(x\right)={\displaystyle {\sum }_{i=1}^N\left({\beta }_i^{*}-{\beta }_i\right)K\left(x_i,x\right)}+b$ (3)

其中 $\left({\beta }_i^{*}-{\beta }_i\right)\ne 0$ 为训练样本支持向量， $K\left(x_i,x\right)$ 为核函数，根据Mercer条件，存在映射函数 $\phi \left(x\right)$ 和核函数 $K\left(x_i,x\right)$，使得满足：

$K\left(x_i,x_j\right)=\phi \left(x_j\right)\circ \phi \left(x_i^{\text{T}}\right)$ (4)

在实际应用中，常见的核函数有以下四种类型：

$K_1\left(x_i,x_j\right)=x_i{x}_j^{\text{T}}$ (5)

$K_2\left(x_i,x_j\right)={\left(t+c{x}_i{x}_j^{\text{T}}\right)}^d$ (6)

$K_3\left(x_i,x_j\right)=\exp \left(-\frac{{\Vert x_i-x_j\Vert }^2}{2{\sigma }^2}\right)$ (7)

$K_4\left(x_i,x_j\right)=\tanh \left[\alpha \left(x_i{x}_j^{\text{T}}+\beta \right)\right]$ (8)

以上公式(5)是线性核函数，在线性核函数中没有参数；公式(6)是多项式核函数，其中的参数 是斜率， 是多项式维数；公式(7)是高斯核函数，其中的参数 $\sigma$ 在SVR性能中起着主要作用，如果估计过大核函数将呈线性，高维投影失去其非线性功率，如果估计过小，核函数就缺乏正则化；公式(8)是Sigmoid 型核函数，其中 $\alpha$ 是幅度调整参数， $\beta$ 是控制映射阈值位移参数。

SVR的性能主要取决于三个因素：1) 核函数的类型及其核函数参数；2) SVR模型中惩罚系数 和不敏感损失函数的参数 $\epsilon$ ；3) 建模数据集的特征信息。首先核函数类型的选择是决定的SVR模型的主要因素，核函数是反映数据的先验知识，决定训练数据高维特征空间情况，不恰当的核函数会使得训练样本在高维空间的分布变得比输入空间的分布更复杂，核函数的构造对于特定的核方法固然重要，但当核函数构造完毕(核函数的类型固定)后，其次核函数中的参数最优匹配同等重要。研究表明，针对同一个核函数，选择不同的核函数的参数，SVR的泛化性能会相差很大 [16]，这主要是因为不同的参数对应的高维特征空间的结构具有差异性，而特征空间的性质直接决定着核方法的性能。再次SVR模型的惩罚系数和不敏感损失函数参数也是两个重要参数，其中惩罚系数控制着最小训练误差和最小化模型复杂度之间的平衡，目的是在总体误差与学习机模型复杂性之间进行折衷，即在确定的特征空间中调节经验风险和学习机置信范围的比例，以使得学习机器的泛化能力最好，而不敏感损失函数参数是度量训练点上误差的代价，在模型的光滑性和泛化性之间起着平衡作用 [17] [18] [19] [20]。最后建模数据最优特征信息选择对SVR模型性能有一定的影响，由于建模因子数据在收集中包含有噪声，维数高，而且数据是多数据源或异构数据集，如果不对原始建模因子数据做特征提取处理，将会影响SVR的性能，增加模型的复杂度影响模型泛化性能 [21] [22] [23] [24]。

由于核函数的类型及其核函数参数，支持向量回归模型中惩罚系数C和不敏感损失函数的参数 $\epsilon$，以及建模数据的特征信息之间它们相互依赖，相互影响，在实际建模应有中需要同时考虑混合优化，才可以选择最为适用的模型，但是目前的研究文献主要是针对特征信息提取，或者核函数的类型及其核参数进行优化，或者针对惩罚系数C和不敏感损失函数的参数 $\epsilon$ 进行优化，如Huang和Wang在核函数类型为高斯核函数前提下，提出利用遗传算法同时优化特征子集和SVR模型参数 [25] 极大提高分类准确率，高斯核函数参数采用交叉验证方法确定，论文没有对其它类型核函数选择优化；Oliveira和Braga提出利用粒子群算法优化选择训练数据特征和高斯核函数的参数，并以此建立软件工程量需求预测模型，取得较高得准确率，但是该论文没有对SVR模型的参数进行优化 [26]；Li Xiaofeng和Wu Shijing等人利用粒子群算法优化支持向量机的惩罚系数C和高斯核函数的 $\sigma$ 建立高压断路器机械故障诊断，取得很好的效果，但是没有选择特征函数和优化其他参数 [27]。Yang Ailing和Li Weide等利用自相关函数提取输入信息特征，并利用灰狼算法和交叉验证优化最小二乘支持向量回归模型参数，建立短期电力负荷预测模型，实验室结果显示相对传统时间序列模型该方法能提高预测精度 [28]，但是对特征选择和模型参数没有优化。为此，本文利用粒子群–模拟退火算法构造混合进化算法技术，优化选择最佳的建模数据的特征，协同进化支持向量机的核函数类型以及参数，相应匹配最优模型参数，开展协同进化支持向量机径流预测建模研究，达到充分挖掘建模数据的有效特征信息，对不同的数据属性自适应选择不同的核函数类型，核函数的参数和模型参数。

2.2. 粒子群优化和模拟退火算法

粒子群优化(Particle Swarm Optimization, PSO)是由Kennedy和Eberhart在1995年提出的一种基于群体智能方法的进化计算技术，其思想主要来源于自然界中鸟群等生物种群觅食行为的仿真，它是通过个体之间的信息交换，互动协作来搜寻全局最优解，其算法简单、易实现同时又有深刻的群体智能背景，因此，在短短十几年间，获得了很快的发展，出现大量的研究成果，并在函数优化、神经网络训练、模式分类、模糊系统控制以及其他工程领域得到了广泛的应用 [29]。但它也有缺陷，如容易早熟，易陷入局部极值点，在进化后期粒子种群容易失去多样性，优化精度较差。因此，许多研究者提出了大量的改进算法，这些改进算法在一定程度上改善了基本粒子群算法的性能 [30]，粒子群算法具体运算流程如图1所示。

Figure 1. Flow chart of PSO

图1. 粒子群优化算法流程图

模拟退火算法(Simulated Annealing, SA)最早的思想是由N. Metropolis等人于1953年提出。1983年S. Kirkpatrick等成功地将退火思想引入到组合优化领域 [31]，它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。在迭代过程中不像粒子群算法只是用更好的值来代替原来的位置，在SA算法中伴随温度参数的不断下降，是以概率接受新状态在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优 [32] [33] [34]，模拟退火算法运算流程如图2所示。

Figure 2. Flow chart of SA

图2. 模拟退火算法流程图

2.3. 粒子群–模拟退火算法协同进化支持向量回归建模

对于给定样本 $\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right),x_i\in R^n,y_i\in R\right\}$，其中n为影响径流变量因子个数，N是样本个数，为此把选取的建模数数据分成训练数据集 $\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_{N_1},y_{N_1}\right),x_i\in R^n,y_i\in R\right\}$ 和测试数据 $\left\{\left(x_{N_1+1},y_{N_1+1}\right),\left(x_{T+2},y_{T+2}\right),\cdots ,\left(x_N,y_N\right),x_i\in R^n,y_i\in R\right\}$，为此定义适应度函数为：

$f\left(T\right)=\frac{1}{N_1}{\displaystyle {\sum }_{i=1}^{N_1}{\left(y_i-{\hat{y}}_i\right)}^2}$ (9)

本文是利用粒子群–模拟退火算法构造协同进化算法优化选择训练数据集的特征，核函数类型及其参数，支持向量参数，其数学模型为最大最小化离散随机动态规划问题：

$\{\begin{array}{l}\max f\left(T\right)=\frac{1}{N_1}{\displaystyle {\sum }_{i=1}^{N_1}{\left(y_i-{\hat{y}}_i\right)}^2}\\ s.b.{\hat{y}}_i={\displaystyle {\sum }_{i=1}^{N_1}\left({\beta }_i^{\text{*}}-{\beta }_i\right)K\left(c_i{x}_i,x\right)}+b\\ \{\begin{array}{l}\min \left(\omega ,\xi ,{\xi }^{\text{*}}\right)=\frac{1}{2}{\omega }^{\text{T}}\omega +C{\displaystyle {\sum }_{i=1}^N\left(\xi +{\xi }^{\text{*}}\right)}\\ s\text{.}b\text{.}{y}_i-{\omega }^{\text{T}}\phi \left(x_i\right)-b\le \epsilon +\xi \\ -y_i+{\omega }^{\text{T}}\phi \left(x_i\right)+b\le \epsilon +{\xi }^{\text{*}}\\ \xi ,{\xi }^{\text{*}}\ge 0,i=1,2,\cdots ,N\end{array}\\ c_i\in \left\{0,1\right\},i=1,2,\cdots N_1\\ K_j\in \left\{K_1,K_2,K_3,K_4\right\}\end{array}$ (10)

由于混合模型需要进化选择变量和核函数类型，优化对应核函数参数和模型参数，为此本文编码采用0-1布尔代数和浮点数混合编码方法，其中0-1编码主要控制变量选择和核函数类型，浮点数编码主要控制核函数参数和支持向量参数大小，控制变量选择编码0表示该变量没有选中，1表示该变量被选中；控制核函数选择00表示线性核函数、01表示多项式核函数、10表示高斯核函数、11表示Sigmoid核函数；所有0-1编码形成整数编码串，浮点数R₁和R₂对应核函数参数编码，R₃和R₄则对应SVR模型参数编码，所有浮点数形成浮点数编码串，具体构成和表示见表1。

Table 1. Relevant parameter coding components involved in the SVR model

表1. SVR模型所涉及的相关参数编码构成

粒子群–模拟退火混合进化SVR的具体实现步骤如下：

1) 参数初始化，随机生成n行 $m_1$ 列布尔代数矩阵和n行 $m_2$ 列浮点数矩阵，n表示种群个数，本文n = 40，粒子群种群个数40个， $m_1$ 是影响径流变量建模因子个数和四个核函数决定，为此 $m_1=N+4$， $m_2$ 是核函数参数个数和模型参数决定，故此 $m_2=4$。布尔代数是控制矩阵，控制变量选择和核函数类型，浮点数矩阵取上的 $\left[0,10\right]$ 均匀分布随机数，它控制核函数的参数和SVR模型参数的大小。

2) 计算适应度，输入训练样本并标准化，通过解码每行布尔代数矩阵和浮点数矩阵，即可获得参与计算建模样本因子、核函数类型、核函数参数和模型参数，输入相应选择建模样本的特征，通过(10)式计算每个粒子的适应度，比较种群个体的适应度获得最好位置 $p_{best}\left(t\right)$，以及群体中全局的最好位置 $p_{gest}\left(t\right)$。

3) 粒子速度更新方程为：

$v_i^{t+1}=\omega v_i^t+c_1{r}_1\left(p_{best}\left(t\right)-s_i^t\right)+c_2{r}_2\left(p_{gbest}\left(t\right)-s_i^t\right)$ (11)

$\omega ={\omega }_{\max }-\frac{{\omega }_{\max }-{\omega }_{\min }}{ite{r}_{\max }}\cdot iter$ (12)

其中 ${\omega }_{\max },{\omega }_{\min }$ 分别是惯性权重的最大值和最小值， $iter,ite{r}_{\max }$ 分别是当前迭代次数和最大的迭代次数， $c_1,c_2$ 是学习因子， $r_1,r_2$ 是随机常数。

4) 粒子个体位置更新分为二进制离散粒子群和实数粒子群的更新，二进制离散粒子群位置更新方程为：

$s_i^{t+1}=\{\begin{array}{l}0,r\ge \frac{1}{1+\exp \left(-v_i^{t+1}\right)}\\ 1,r<\frac{1}{1+\exp \left(-v_i^{t+1}\right)}\end{array}$ (13)

其中，r为 $\left[0,\text{1}\right]$ 均匀分布的随机数。实数粒子群位置更新方程为：

$s_i^{t+1}=s_i^t+v_i^{t+1}$ (14)

5) 计算新的位置和旧的位置适应度之差 $\Delta f=f\left(s_i^{t+1}\right)-f\left(s_i^t\right)$，若适应度变大，则新的位置被接受，作为下一代的粒子，若适应度变小，对其进行模拟退火Metropolis抽样准则接收进入下一代。在 $\Delta f<0$ 时，在 $\left[0,\text{1}\right]$ 均匀分布生成的随机数R，在当前温度 $T_i$ 下，如果 $R>{\text{e}}^{\left(\Delta f/T_i\right)}$，则接收到下一代 $s_i^{t+1}$，否则，在当前温度 $T_i$ 下，对其粒子速度高斯扰动，产生新的速度，并以此更新位置，使其达到抽样稳定准则。

6) 反复进行2)~5)，直到适应度满足要求或者达到总的进化代数(总的进化代数)。

7) 把进化后的最后一代适应度最高个体解码，得到相应SVR模型建模样本的特征、核函数的类型、核函数的参数和模型参数，输入测试样本进行预测，HPSOSA-SVR算法的流程框架如图3所示：

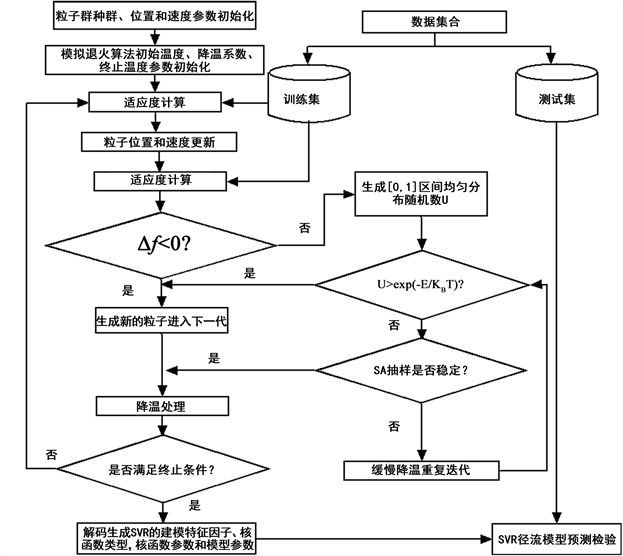
Figure 3. Flow chart of the HPSOSA-SVR algorithm

图3. HPSOSA-SVR算法的流程图

3. 应用实例及其结果分析

3.1. 建模数据

广西柳江属珠江水系，干流全长773.3公里，流域面积57,173平方公里，跨黔、桂、湘三省30个县、市，天然落差1306米，平均比降1.68‰，年均流量1865立方米/秒，每年4~9月为汛期。从1988年至今的近20年间，大洪水的发生较为频繁，灾害也很严重，发生超过100年一遇的特大洪水1次(“1996.7”)，20至50年一遇的大洪水3次(“1988.8”、“1994.6”和“2004.7”洪水)，10至20年一遇的较大洪水1次(“2000.6”洪水)，建立精度较高的柳江汛期径流预测模型对防灾减灾具有重要意义。

为此本文建模数据选取广西柳江老桥口的每天12时的径流数据进行应用实例分析，总的数据为2006年1月1日到2010年12月31日共1826个数据，分别建立2008年，2009年和2010年4~9月汛期径流预测，依据建模需要把数据分为训练数据和测试数据，训练数据用于建立径流拟合模型，测试数据用于检验模型预测效果，具体如表2所示。

Table 2. Establish model training data and test model test data

表2. 建立模型的训练数据和检验模型的检测数据

3.2. 建模因子

径流模型选择自变量对于预报模型非常重要。首先本文采用对区域径流有显著影响的降水、水汽、动力和热力等四类因子作为候选因子，从中国气象局96小时T213数值产品的17种常规气象要素和物理要素，数据覆盖柳江径流，范围从150 N到300 N，经度从1000 E到1200 E，分辨率为10˚ × 10˚，共有336个网格点因子，经过初步筛选获得45个候选因子，对候选因子通过协同进化选择特征变量作为建模因子建立柳江径流模型。

3.3. 模型参数和性能评价

为考察HPSOSA-SVR模型的效果，分别建立支持向量回归(SVR)模型、单纯粒子群进化支持向量回归模型(PSO-SVR)，SVR模型采用高斯核函数，其所有参数确定采用交叉验证确定，PSO-SVR是利用粒子群优化选择训练数据集的特征，核函数类型及其参数建立径流模型，其中两个进化模型参数为粒子群个数40，进化迭代次数200，模拟退火算法初始温度1000，降温系数0.9。模型分别对821个样本拟合和对183个样本预测，比较结果用来检验预测模型的效果。设和分别表示实际值和神经网络集成输出，为样本个数，根据数理统计的基本原理，采用4个指标来检验模型的拟合和预测效果。引入以下4种统计指标：

1) 均方根误差(Root Mean Square Error, RMSE)：

$RMSE=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left(y_t-{\hat{y}}_t\right)}^2}}$ (15)

2) 平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)：

$MAPE=\frac{100}{n}{\displaystyle {\sum }_{t=1}^n\frac{\left|y_t-{\hat{y}}_t\right|}{\left|y_t\right|}}$ (16)

3) 纳什效率系数(Nash-Sutcliffe Efficiency coefficient, NSE)：

$SE=1-\frac{{\displaystyle {\sum }_{t=1}^n{\left(y_t-{\hat{y}}_t\right)}^2}}{{\displaystyle {\sum }_{t=1}^n{\left(y_t-\hat{y}\right)}^2}}$ (17)

式(15)~(17)中， $y_t,{\hat{y}}_t$ 分别代表径流实际值和模型的输出值，n为样本个数，在纳什效率系数的基础上，提出洪水峰值模型预测性能评价指标：

4) 峰值纳什效率系数

$NS{E}_{peak}=1-\frac{{\displaystyle {\sum }_{i=1}^p{\left(y_{pi}-{\hat{y}}_{pi}\right)}^2}}{{\displaystyle {\sum }_{i=1}^p{\left(y_{pi}-{\hat{y}}_{pi}\right)}^2}}$ (18)

式(18)中、 $y_{pi},{\hat{y}}_{pi}$ 分别表示洪水峰值实际值和预测洪水峰值输出值， ${\bar{y}}_{pi}$ 表示洪水峰值的平均值，本文把径流大于4000 (m³/s)看作是洪峰值，p为洪水峰值期间样本个数。性能评价指标(1)和(2)主要是从数值上评价模型的性能，其值越小说明模型的预测性能越好；性能指标(3)主要是看模型能否对径流的趋势做出正确的判断，其值越大就说明模型的可信度高，能够准确跟踪径流趋势；性能指标(4)是洪水峰值趋势的判断指标，对于径流模型在实际应用中，最关心的就是能否较为准确预测灾害性洪水，即洪水峰值达到时刻和对洪水峰值趋势跟踪。

3.4. 结果分析

图4是HPSOSA和PSO分别进化SVR过程中，适应度随迭代次数变化过程。从图4可以看出，在200次迭代次数过程中，HPSOSA-SVR前60次中出现振荡情况，之后随着迭代次数增加适应度逐渐趋于变小而且稳定，而PSO-SVR在进化过程前140次还在反复振荡，直到迭代200次还没有趋于稳定状态。从图4迭次次数和适应度变化过程可以看出，HPSOSA-SVR随着训练次数的增加，适应度逐渐稳定，避免过早收敛的问题并避免局部最优。

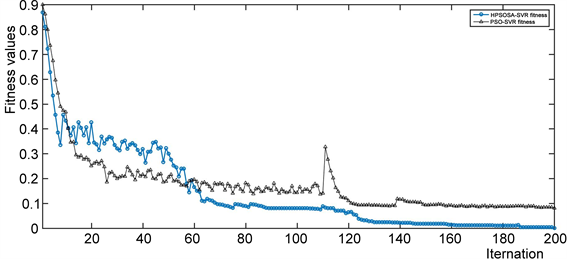
Figure 4. Fitness values of PSO-SVR and HPSOSA-SVR process with the iterations

图4. HPSOSA-SVR和PSO-SVR进化迭代过程中适应度变化过程

Table 3. Fitting and prediction results of three models during the 2008 flood season

表3. 三种模型对2008年汛期的拟合和预测结果

注：拟合数据中径流大于4000的峰值为47个，预测数据中径流大于4000的峰值是24个。

表3是三种模型对柳江径流对2006年1月1日~2008年3月31日期间的821建模样本拟合和对2008年4月1日~9月30日共183个样本预测的各种性能统计表，图5是三种模型对2008年4月1日~9月30日期间径流预测效果图，图6是对2008年4月1日~9月30日期间径流大于4000 (m³/s)预测效果。

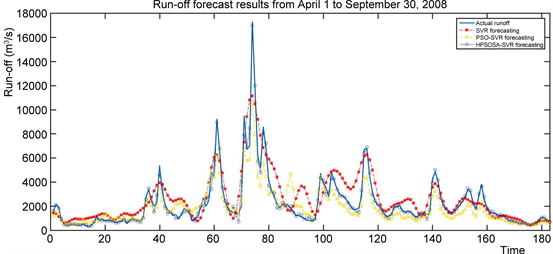
Figure 5. Prediction results of runoff from April 1 to September 30, 2008

图5. 不同模型对2008年4月1日~9月30日径流预测结果

Figure 6. Prediction results on runoff greater than 4000 (m³/s) from April 1 to September 30, 2008

图6. 2008年4月1日~9月30日径流大于4000 (m³/s)预测结果

表4是三种模型对柳江径流2007年1月1日~2009年3月31日期间的821训练样本拟合和对2009年4月1日~9月30日期间共183个样本预测的误差性能统计表，图7是三种模型对2009年4月1日~9月30日期间径流预测效果，图8是对2009年4月1日~9月30日期间径流大于4000 (m³/s)预测效果。

Table 4. Fitting and prediction results of three models during the 2009 flood season

表4. 三种模型对2009年汛期的拟合和预测结果

注：拟合数据中径流大于4000的峰值为49个，预测数据中径流大于4000的峰值是19个。

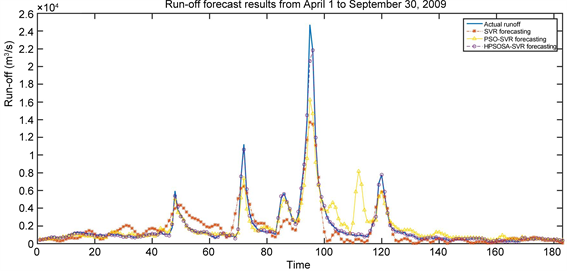
Figure 7. Prediction results of runoff from April 1 to September 30, 2009

图7. 不同模型对2009年4月1日~9月30日径流预测结果

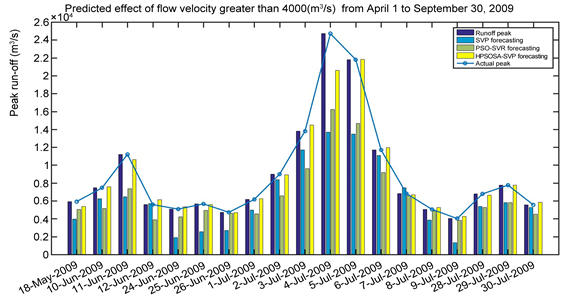
Figure 8. Prediction results on runoff greater than 4000 (m³/s) from April 1 to September 30, 2009

图8. 2009年4月1日~9月30日径流大于4000 (m³/s)预测结果

表5是两种模型对柳江径流在2008年1月1日~2010年3月31日期间的821训练样本拟合和对2010年4月1日~9月30日共183个样本预测的各种误差统计，图9是三种模型对2010年4月1日~9月30日径流预测效果，图10是2010年4月1日~9月30日径流大于4000 (m³/s)预测效果。

Table 5. Fitting and prediction results of three models during the 2010 flood season

表5. 三种模型对2010年汛期的拟合和预测结果

注：拟合数据中径流大于4000的峰值为48个，预测数据中径流大于4000的峰值是21个。

Figure 9. Prediction results of runoff from April 1 to September 30, 2010

图9. 不同模型对2010年4月1日~9月30日径流预测结果

Figure 10. Prediction results on runoff greater than 4000 (m³/s) from April 1 to September 30, 2010

图10. 2010年4月1日~9月30日径流大于4000 (m³/s)预测结果

从表3，表4和表5的结果可以看出HPSOSA-SVR模型对训练样本拟合和和测试样本预测的RMSE和MAPE和性能指标均小于SVR、PSO-SVR模型，说明HPSOSA-SVR模型拟合值和真实值，预测值和真实值之间的偏离程度小，拟合精度和预测高于SVR、PSO-SVR模型；同时可以看出SVR-PSOSA模型对训练样本和测试样本的NSE和NSE_peak性能指标均大于SVR、PSO-SVR模型，说明SVR-PSOSA能够准确把握汛期径流的趋势，这些显示出SVR-PSOSA模型相对SVR模型、PSO-SVR具有很好的学习能力和预测能力。进一步从图5~10可以看出，PSO-SVR性能优于SVR模型，这进一步说明在实际应用中需要对SVR模型进一步优化，提高SVR模型拟合和预测精度。

洪水峰值性能指标是预测灾害性洪水达到时刻和对洪水峰值趋势跟踪重要指标，也是检验模型能否预测灾害性洪水以及在实际应用的重要指标。从表3的结果可以看出，在对2006年1月至2008年3月建模样本拟合中SVR的峰值纳什效率系数是0.8754，PSO-SVR的峰值纳什效率系数是0.8921，HPSOSA-SVR的峰值纳什效率系数是0.9526，三者相差不大；但是建立的模型对2008年4月~9月样本预测时，SVR的峰值纳什效率系数仅为0.4539，PSO-SVR的峰值纳什效率系数为0.3757，HPSOSA-SVR的预测峰值系数是0.9447，三者相差特别悬殊，SVR、PSO-SVR模型基本不能在实际应用中预测洪水峰值，而HPSOSA-SVR可以对洪水峰值做出精度很高的预测。同时从图6也可以看出，HPSOSA-SVR模型能够对2008年汛期径流大于4000 (m³/s)峰值趋势很好的跟踪。同样HPSOSA-SVR模型在对2009年和2010年汛期峰值预测中，对汛期洪水峰值趋势很好的跟踪能力，这些结果均说明HPSOSA-SVR模型用于预测灾害性洪水可信度很高，而且结果稳定。

表6给出HPSOSA协同进化支持向量回归得到核函数类型，核函数的参数和支持向量回归的参数，从表6可以看出，三种不同数据的径流模型，通过粒子群–模拟退火算法协同进化支持向量回归的核函数，都得的核函数类型为Sigmoid型核函数，以及核函数参数和模型参数，表6的结果说明Sigmoid型核函数最为适宜用于建立柳江汛期径流SVR预测模型，而且预测结果精度高，稳定性好。

Table 6. Fitting and prediction results of three models during the 2010 flood season

表6. 三种模型对2010年汛期的拟合和预测结果

4. 结语

径流是水文系统中研究人员关注的重大课题，它关系到水利工程建设和水资源的开发利用，并且由于径流系统包含着系统空间和时间变化的非线性特性，传统的分析方法很难对它们的演化规律和变化特征做出清晰的了解和准确的预测。本文利用粒子群算法和模拟退火算法构造协同进化算法，同时选择建模数据的特征、协同选择核函数类型、优化核函数及其核函数的参数，建立柳江径流预测模型，实例计算结果得出以下结论：

1) HPSOSA-SVR算法能避免局部最优解，通过混合SA的接受准则和PSO随机接受原则，减少了局部搜索端点附近的震动偏离；根据新旧位置之间不同的适应度值，运用规则决定是接受新位置，还是重新计算另一个可信位置。这使得模型可以跳出局部最优解，并减少局部搜索终点附近的震动偏离。这些特性提高了解决方案的质量和收敛速度。

2) HPSOSA-SVR算法具有运算速度快和能在全局方向搜索最优解的优点，通过结合PSO运行机制、并行处理干扰机制以及SA解决搜索路径的特点，形成了一个良好的质量解决方案。

3) 根据本文的研究结果，我们可以得出以下结论：Sigmoid曲线核函数的SVR模型可以作为实际径流预测应用中的一种有效的核函数，而且最为适宜汛期径流SVR预测模型，预测结果精度高，稳定性好。

4) 采用Sigmoid核函数时，支持向量回归实现的是一种前向神经网络，但是由于使用SVM方法，网络隐含层节点数、连接权值都是在设计的过程中进化确定，而且SVR的理论决定了它最终求得的是全局最优值而不是局部最小值，也保证了它对于未知样本的良好泛化能力而不会出现过学习现象，以此可以解释Sigmoid曲线核函数的SVR模型最为适宜径流预测模型。

基金项目

国家自然科学基金资助项目(41575051、41565005)，广西科技厅科技基地和人才专项(No. AD16450003)，广西科技厅创新项目(No. 2018AB14003)，广西高校中青年教师基础能力提升项目(No. 2018KY0699、2018KY0700、2018KY0701)，广西来宾市科学研究与技术开发项目(来科能193305)。