1. 研究背景
在信息化时代背景下，人们获取信息的途径和方式变得多元化，学生的学习方式也变得多元化，课堂教学不在是教师与学生之间唯一的“教与学”之间的关系，传统的课堂教学方式受到了新的挑战。美国的可汗学院将“视频再造教育”的“翻转课堂”推向了教育界关注的热点，被称为“未来的教育” [1]。基于此，国内很多专家和学者对“翻转课堂”的教学形式展开了论述和实践。如：学者张旸、蒙泽察在文献 [2] 中对“导学案教学”与“翻转课堂”的价值进行了探讨。专家汪晓东在文献 [3] 中对“翻转课堂”的实践困惑提出了应对的措施和解决的方案，在文献 [4] 中对翻转课堂的前世今生进行了叙述。对于“翻转课堂”在高职数学教学中的研究，也有部分高校的教师对此进行了研究 [5] - [10]。
两个重要极限是高等数学或者经济数学教学中重要的教学内容。对于高职院校的学生，不需要去了解两个重要极限的证明过程，但需要懂得运用两个重要极限的公式求解函数的极限运算。目前，高职院校生源来源方式比较多，有高考生、单招生、对口生，等。对于两个重要极限公式的运算，运用旧的学习方法，高考生也可以接受。但对于单招生、对口生，他们比较困难于运用两个重要极限的公式求解函数的极限。基于此，有不少的学者对此进行了研究 [11] [12]。
本文从信息化的视角对两个重要极限的教学策略进行了研究，运用翻转课堂的教学形式对教学策略进行研究，且对两个重要极限的教学方法提出了一些新的见解。
2. 课堂教学策略设计与教学方法的研究
本文以2019级云计算技术与应用2班和2019级制冷与空调技术1班为例，运用翻转课堂的教学形式对高等数学课程中两个重要极限的教学策略和方法进行研究。教学流程见图1。
学情分析：2019级云计算技术与应用2班共44人，其中高考生31人，对口生13人；2019级制冷与空调技术1班共29人，其中高考生6人，单招生14人，对口生9人。
课前：针对两个重要极限的知识点内容，教师首先给出三个维度(知识与技能、过程与方法、情感态度与价值观)的教学目标。接着将教学目标分解为两个二阶目标，即掌握第一个重要极限公式的运用和掌握第二个重要极限公式的运用。将两个重要极限知识点的课前学习指南、微课、学习资料发布到学习平台上，给予学生发布两个重要极限知识点的课前作业。最后，学生通过网络学习平台观看教学视频和资料，完成课前作业。经过统计得出：2019级云计算技术与应用2班学生观看视频完成率为70%，课前作业平均分为65分，2019级制冷与空调技术1班学生观看视频完成率为65%，课前作业平均分为56分。
课中：两个重要极限课程知识点授课2~3个课时，教学实施过程具体如下，见图2。
Figure 1. The basic teaching flow chart of “flipped classroom”
图1. “翻转课堂”的基本教学流程图
Figure 2. Flow chart of classroom teaching implementation
图2. 课堂教学实施流程图
第一步，对课前学生观看视频和完成作业的情况进行反馈，给予学生指出问题所在。
第二步，运用信息化技术MATLAB软件展示第一个重要极限结果等于1的过程，使得学生明白为
什么第一个重要极限的结果等于1，而不是需要证明第一个重要极限的结果等于1，即
。具体
程序和图像如下，见图3：
程序：在命令窗口中输入
>> syms x y
>>x=-20*pi:0.001:20*pi;
>> y=sin(x)./x;
>> plot(x,y)
>>xlabel('x')
>>ylabel('y')
>>title('sin(x)/x')
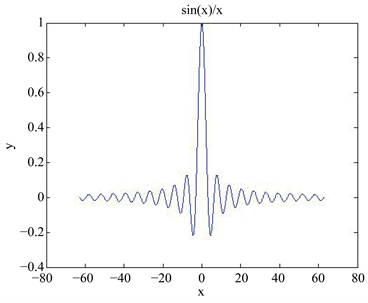
Figure 3. The graph of the first important limit
图3. 第一个重要极限的函数图像
为了能够让学生懂得运用第一个重要极限的公式求解函数极限，经过经验总结，给出了以下四个公式，教会学生观察公式，运用“缺什么，补什么”的思想对类似函数极限进行求解。
，
，
，
。
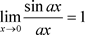例1：
，为了求解该函数极限，对照第一个公式，学生会观察得到分母缺少了5。因此，将会给分母补充系数5。为了等价，分子也补充系数5，最终结果等于5。
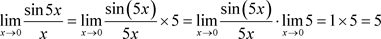
第三步，布置学生做能够运用第一个重要极限公式求解其他函数极限的练习，同时教师给予还不懂的学生进行个性化辅导和对练习进行讲评。
第四步，展示第二个重要极限的函数，指出该函数为幂指函数。给予学生提出问题，幂指函数的极限等于多少呢？
第五步，运用信息化技术MATLAB软件展示第二个重要极限结果等于e的过程，即
。
给予学生明白第二个重要极限为什么等于e，而不是需要证明该函数极限的结果等于e。具体程序和操作过程如下：
程序：在命令窗口中输入
>> syms x y
>> y=(1+2/x)^x;
>> limit(y,x,a)
在操作过程中，分别让a = 10，100，100……，或者a = −10，−100，−1000……。就可以得到如下表格的结果，见表1：
Table 1. Process analysis of the second important limit solution
表1. 第二个重要极限求解的过程分析
由于第二个重要极限—幂指函数极限等于e的公式比较难于让学生运用，即第二个重要极限知识点的运用是本次课的一个难点。为了解决这个问题，经过多年的教学，总结出了幂指函数等于e的三个步骤给予学生进行理解和运用，具体如下：
(1) 底数是否有1+；
(2) 自变量趋向于0或者趋向于无穷大时，“括号内1 + 后面的函数”是否趋向于0；
(3) “括号内1+后面的函数”与指数是否为互为倒数，即相乘等于1。
具体教学过程运用如下：
例2 求下列函数的极限
学生在做题过程中，不清楚该幂指函数如何进行计算，即不会运用第二个重要极限对此进行求解。我们可以根据幂指函数的三个步骤进行计算：第一，底数是否有1+；可以看出该幂指函数的底数是1−，
而不是1+。为了计算出结果，我们把1-改为1+，即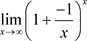
。第二，自变量趋向于0或者趋向于无穷大时，“括号内1 + 后面的函数”是否趋向于0；可以看出x趋向于无穷大时，“括号内1 + 后面的函数”为
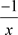已经趋向于0了，即满足第二。第三，“括号内1 + 后面的函数”与指数是否为互为倒数，即相乘等于1；第二的时候已经清楚“括号内1+后面的函数”为
，该函数的倒数应该是
，即给予指数部分添加
，
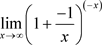，该函数的极限等于e。由于例2中幂指函数的指数部分是x不是
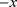，为了等价，需要给予指数部分添加负号，即
。因此，例2幂指函数的极限为e−1.
例3 求下列函数的极限
根据幂指函数的三个步骤进行计算：
第一，底数是否有1+；可以看出该幂指函数的底数已经有1+，因此第一已经满足。
第二，自变量趋向于0或者趋向于无穷大时，“括号内1 + 后面的函数”是否趋向于0；可以看出x趋向于无穷大时，“括号内1 + 后面的函数”为
已经趋向于0了，即满足第二。
第三，“括号内1 + 后面的函数”与指数是否为互为倒数，即相乘等于1；第二的时候已经清楚“括号内1 + 后面的函数”为
，该函数的倒数应该是
，即给予指数部分添加
，
，该函数的极限等于e。由于例3中幂指函数的指数部分是x不是
，为了等价，需要给予指数部分乘以3，即
。因此，例3幂指函数的极限为e3。
第六步，教师讲授幂指函数求解极限的其他例题，布置学生做第二个重要极限的练习，同时给予还不懂的学生进行个性化辅导和对练习进行讲评。
第七步，通过网络学习平台运用随机选题的方式布置学生做课堂检测作业。经过统计得出：对于两个重要极限知识点的检测，2019级云计算技术与应用2班学生检测结果由平均分为65分变为83分，2019级制冷与空调技术1班学生检测结果由平均分为56分变为75分。
第八步，教师对学生课堂检测作业正确率低于80%的题目进行讲评。
第九步，课堂小结。
课后：运用网络学习平台，教师与学生进行交流。对于还有不明白知识点的学生，则通过网络学习平台群聊、话题留言等功能对学生的疑惑进行解答。
3. 研究结论
翻转课堂的教学模式可以提高学生的学习效果。从检测结果可以看出，不管班级中高考生的数量多，还是单招生和对口生的数量多，运用翻转课堂的教学模式都可以使得成绩得到提高，只不过提高的幅度不一样而已。本文从信息化的视角对两个重要极限的教学策略和方法进行研究，促进学生学习成绩提高的原因可能有以下几点：
1. 翻转课堂使得学生的学习目标和教师的教学目标更加明确。
采用传统的教学方法进行授课，教师在课堂上把学习的重难点讲解完。对于基础不好的高职生来说，犹如“水过鸭背”一样，不清楚教师在课堂上讲什么，没能抓住学习的目标。
采用翻转课堂的教学方法进行授课。课前，教师设计学生的学习指南、习题、课前作业、检测作业、课程设计总表及课程教学设计等资源。第一，学生通过网络学习平台观看教学视频，完成课前作业。课堂上学生就比较清楚地明白本次课的学习目标，也比较清楚地了解到自己所遇到的难点在哪里。教师在授课过程中，讲授到该难点的时候，他们的注意力将会更加集中，学习的效果更佳。第二，教师通过批改学生课前的作业，可以发现学生在学习知识点的问题和难点。课堂上根据学生的问题和难点，讲解知识点，达到“以学定教”的目的。
2. 两个重要极限的教学方法使得学生更加容易接受。
在讲解两个重要极限的知识点时，传统的教学方法给出它们的结果，接着直接运用公式去求解极限，学生往往比较困难理解为什么该函数极限的结果。然而，在讲解第一个重要极限的时候，本文采用“套公式”的方式给予学生进行教学，即给出第一个重要极限的四个拓展公式，学生比较容易接受所求解函数极限的结果。在讲解第二个重要极限的时候，本文给出了公式理解的三个步骤，即幂指函数求取极限的三个步骤。对于幂指函数求取极限，学生只要对照三个步骤进行构造函数就可以了，相对来说，比较容易进行理解。
3. 运用信息化手段MATLAB软件帮助学生实现空间想象力。
传统的教学方法在解释两个重要极限结果的过程中，往往喜欢运用证明的方式进行。对于基础比较薄弱的高职生而言，证明往往是他们的噩梦，激发不起他们的积极性，反而使得课堂效率低下，也不符合高职院校数学知识“必须、够用”的原则。为了解决该问题，对于知识点的理解，使得学生可以绕过公式的证明，又明白公式的结果为什么是这样。本文采用信息化手段MATLAB软件对两个重要极限的结果由来进行仿真验证，让学生明白了这两个公式的结果为什么是这样，帮助他们实现空间的想象力。
4. 运用网络学习平台随机选题和乱序的方式给予学生布置作业，可以一定程度检测学生的学习效果。
传统的教学方法在布置作业时候，往往每个学生做的题目都是一样的，这将不可避免的出现很多重复率的作业，达不到检测学生掌握知识的程度。为了解决此类问题，我们在网络学习平台上设置更多的题库。在给予学生布置作业的时候，采用网络学习平台随机选题和乱序的方式，这很大程度上降低了学生做同一道题目的概率，很大程度上可以检测到学生掌握知识的程度。
4. 展望
网络学习平台环境下，本文探讨了如何将信息化手段融入到高职数学中进行教学，同时对两个重要极限知识点的教学方法提出了自己的一些见解。运用两个教学班级做实验进行对比，学生学习成绩得到了很大的提高。最后，从四个方面对学生学习成绩的提高做出了原因分析。在高职数学教学中，对于哪些知识点适合运用信息化的手段进行教学，需要间隔多少个课时对学生进行翻转课堂教学，这是一个需要继续研究的课题，我们将继续对其进行研究。
基金项目
2017年度广西职业教育教学改革研究项目(GXGZJG2017B125)；柳州职业技术学院第九批(2016年)校级教学质量与教学改革工程立项项目A类(2016-A006)。