摘要: 财政收入是国家对经济实行宏观调控的重要经济杠杆，准确预测财政收入对其意义重大，而ARIMA模型是短期预测财政收入的有效工具。以1950~2016年财政收入为样本，建立多组ARIMA模型，进而运多重筛选准则，找到最优滞后阶数p和q，最后确定了最优ARIMA(3,2,8)模型。该模型通过了多项假设检验，对2017~2018年的财政收入进行预测，结论表明预测精度高。同时也利用该模型对2019~2022年的财政收入进行了预测，为国家及政府提供一定的参考价值。
Abstract:
Fiscal revenue is an important economic lever for the state to implement macroeconomic regulation and control. Accurately predicting fiscal revenue is of great significance to it, and the ARIMA model is an effective tool for short-term forecasting of fiscal revenue. Taking the 1950~2016 fiscal revenue as a sample, multiple sets of ARIMA models were established, and then multiple screening criteria were applied to find the optimal lag order p and q. Finally, the optimal ARIMA(3,2,8) model was determined. The model has passed a number of hypothesis tests to predict the fiscal revenue of 2017~2018, and the conclusions indicate that the prediction accuracy is high. At the same time, this model is also used to forecast the fiscal revenue of 2019~2022 in the next few years, providing certain reference value for the country and the government.
1. 引言
财政收入是衡量一个国家经济实力的标志，也是一个国家对经济实行宏观调控的重要手段，财政收入的增长关系着一个国家和社会的经济发展和进步。因此，准确了解财政收入的预测值具有重要的现实意义，能够为政府提供一定的决策 [1]。
2. ARIMA(p,d,q)模型
时间序列分析主要分为三种模型：包括移动平均模型(MA)、自回归模型(AR)、以及自回归移动平均模型(ARMA)。其中AR模型和MA模型是ARMA的一种特殊情况，本文研究的ARIMA模型也是ARMA模型的推广 [2]，ARIMA模型是经过差分后能够将非平稳时间序列转换成平稳的序列，依然适合ARMA模型的称为ARIMA模型。ARIMA模型又称为差分自回归移动平均模型，是著名的时间序列预测分析方法之一，由美国统计学家Box和英国统计学家Jenkins于20世纪70年代初所提出 [3]。原理是将因变量仅对它的滞后值，以及随机误差项的现值和滞后值进行回归，进而建立模型，再次按照ARMA模型的方法进行建立。
3. 建立模型
若
是d阶单整序列，其模型结构如下：
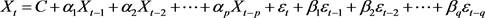
其中C是常数，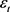
是白噪声，
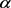和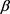
是待估参数，p是自回归模型的最大阶数，而q是移动回归模型的最大阶数。
3.1. ARIMA模型预测步骤
› 步骤1识别
利用相关图和偏相关图，找出适当的p，d和q值
› 步骤2估计
估计回归模型中的自回归和移动平均项的参数
› ›步骤3诊断
对回归模型进行检验，看残差是不是白噪声，如果是就接受拟合模型，反之则从步骤1重新开始做 [4]
› 步骤4预测
利用回归模型进行预测
3.2. 数据来源
数据选自《中国统计年鉴》，本文采用1950~2018年的财政收入总值，其中无国内外债务收入。具体财政收入的时间走势图见图1。
Figure 1. 1950~2018 annual fiscal revenue (100 million yuan)
图1. 1950~2018年度财政收入(亿元)
4. ARIMA模型对财政收入建模
4.1. 财政收入序列平稳性检验
本文采用Eview8.0软件对数据进行统计分析，1950~2018年的财政收入总值数据来源《中国统计年鉴》，财政收入中不包括国内外债务收入。首先对导入的数据财政收入Y取对数，会得到一个新的序列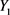
，然后再对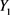
序列进行单位根测验，得知
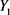序列是不平稳的 [5]，因此对
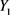进行一阶差分，得到结果如图2，依然不平稳，再进行二阶差分，得到结果如图3，p值等于0，所以财政收入Y是二阶单整。因此建立
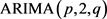模型。
还应该确定一下滞后阶数p和q，然后再进行自相关系数检验，最终确定估计方程。
Figure 2. Sequence stationary test results after first order difference
图2. 一阶差分后序列平稳性检验结果
Figure 3. Sequence stationary test results after second-order difference
图3. 二阶差分后序列平稳性检验结果
4.2. 建立最优的ARIMA模型
从图3中可以看出，自相关系数(AC)和偏相关系数(PAC)的变动没有一个很明显的规则，但可以初步判别从第6阶后逐渐下降。因此根据Akaike info、Schwarz以及Hannan-Quinn准则筛选，进行多种p和q的建模尝试，通过LM检验法、JB统计量检验法、拟合优度检验 [6]，找到最优的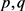
值，分别为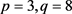
，所以建立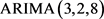
模型 [7]。如下图4：
残差拟合图见图5。
4.3. 拟合优度检验
从图4中可以看出Adjusted R-square值为0.670866，残差拟合图见图5，能够看出残差拟合效果不错，尤其是第57个数据，也就是2005年之后的预测精度是比较准确的。
4.4. 残差正态性检验
对残差进行正态性检验，结果如图6，图中可以看出JB统计量所对应的概率值是大于0.1的置信水平，所以该模型得到的回归方程的残差是服从正态分布。
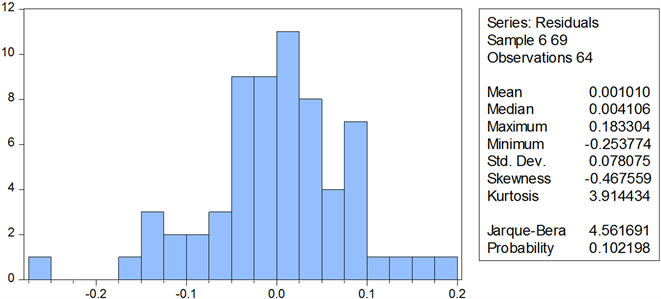
Figure 6.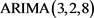 
results of the model's residual normality test
图6.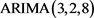
模型的残差正态性检验结果
4.5. 方程显著性检验
从图4能够看出F-statistic的值为12.67378，所对应的概率值p为0，说明该模型通过了F检验。
4.6. 变量显著性检验
从图4中能够看出，在0.05置信水平下，有AR(2)、MA(1)、MA(2)、MA(3)、MA(5)、MA(6)、MA(7)、MA(8)通过了系数显著性t测验，在写回归方程式时，其它的应该从模型方程中剔除。
4.7. 对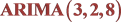
模型进行残差自相关检验(LM检验法)
根据模型的特点，采用LM检验法，该模型自相关检验的结果如下图7。从图7中可以看出F-statistic和Obs*R-square所对应的概率p值分别是0.6735和0.6030，都是大于0.1的显著性水平，因此说明残差不存在序列相关性，为白噪声 [8]。
Figure 7. Residual series autocorrelation test of the model
图7.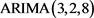
模型的残差序列自相关检验
因此，得到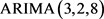
模型的最终的回归方程：
其中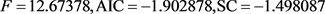
。
5. 模型的预测
利用建立的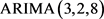
模型对2017~2020年的财政收入进行预测，根据差分反推计算，
(
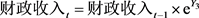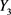表示取对数后的财政收入)进而得到预测 [9]。2017~2018年的财政收入是已知，下表1将年财政收入的真实值与预测值进行对比分析，计算出预测误差率。见表1：
Table 1. Forecasting fiscal revenue forecast for 2016~2022 using models
表1. 利用
模型预测2016~2022年财政收入预测
6. 结论
从表1可以看出，对2017~2018年财政收入模型预测的误差率分别是−3.25%和−7.90%，预测精度比较高。因此对2019~2022年财政收入预测，也是有比较好的预测精度 [10]。
本文研究的模型预测精度较高主要原因有三：第一，选取的数据样本是国家统计局网站上的1950~2018年的财政收入总值，总计样本个数为69个，满足ARIMA模型所需的样本数量；第二，模型分析时也进行了多组试验，并根据AIC和SC准则、LM检验法、JB统计量检验法及拟合优度检验等多重筛选原则，找到适合模型的最优的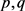
值，进而建立了最优的财政收入预测模型，是
模型 [11]；第三，模型已经通过了多种检验，并且拟合优度较好，残差高度也符合正态分布，且为白噪声。
基金项目
辽宁省自然科学基金指导计划项目(编号：2019-ZD-0471)。