1. 引言
Dota2 (Defense of the Ancients 2)是一个热门的moba类游戏,双方各5人,通过对游戏角色的控制,互相间配合取得游戏的胜利。Dota2中可使用的英雄众多,共100多位,他们的技能、属性、定位等各不相同。本文试通过对这些英雄的数据进行分析,来比较分析结果是否和我们对这些英雄的特点的认知相吻合。
本文数据来源于max+网站,获取了Dota2游戏中116个英雄的9个指标的数据,部分样本数据如下图1:
2. 描述性分析
对游戏中116个英雄的9个指标进行描述性统计分析。这9种指标分别为KDA (Kill Death Assist),胜率,出场次数,经济(每分钟),经验(每分钟),英雄伤害(每分钟),建筑伤害(每分钟),正补(每10分钟),反补(整场),分析的内容包括范围、最小值、最大值、均值和方差。如下表所示:
通过图2的结果可以得出以下结论:
1) KDA (KDA = (杀敌数 + 助攻数)/死亡次数)和胜率这两个指标的方差比较小,最大值和最小值的差异也比较小。这是符合游戏规则的设定的,因为要保证游戏的公平性,所以游戏官方要保证每个英雄的胜率都差不多,维持在50%左右;也要保证每个英雄不会过于强势或劣势,所以各个英雄的KDA的方差也会很小。
2) 其余7个指标的方差还是较大的,这说明该游戏中不同英雄的差异性还是比较大的。这体现出了该游戏中英雄的多样性和趣味性。
3. 系统聚类分析
聚类分析是一种建立分类的多元统计分析方法,能将一批样本或指标数据根据其特征,按照在性质上的亲疏程度在没有先验知识的情况下进行自动分类,产生多个分类结果。同类内部个体特征具有相似性,不同类间个体特征的差异性较大 [1] [2]。
3.1. 对指标的系统聚类
利用SPSS(Statistical Product and Service Solutions)对英雄的各项指标进行聚类分析,以得出各项指标之间的相关关系,聚类结果如下图所示:
分析谱系图3中可以得到以下结论:
根据指标的相关性对指标进行分类可以分为两类,第一类为:经济、正补、经验、英雄伤害、建筑伤害、反补,第二类为:KDA、胜率、出场次数。
第一大类可以看成是与玩家获取的金钱和经验直接相关的指标,可以看成英雄发育程度,但是不对游戏胜利有直接影响。
而第二大类中与胜率绑定在一起的有KDA和出场次数,这个指标的高低可以反应在游戏中玩家所处的状态,KDA越高对游戏局势支援程度越高,获胜概率也就越大;而出场次数和胜率间的关系说明,英雄胜率越高,玩家越愿意选择玩这个英雄,也就是我们常说的版本热门英雄。
3.2. 对样本的K-均值聚类
在系统聚类的基础上,我们根据这两大类指标分别对英雄进行聚类。为了后面对一些英雄进行代表性的分析,不妨选取50位英雄作为样本进行K-均值聚类 [3]。
第一大类指标下的英雄的聚类情况如下:
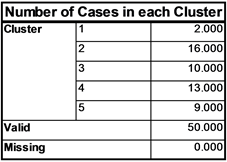
Figure 4. Number of cases in each cluster
图4. 每个聚类中样本的个数
分析上图4和图5,可以得到以下结论:
1) 第二至第五这四类中的英雄的共性还是比较明显的,比如第三类中各个指标值都是相对较低的,通过分析其中的英雄可以发现,第三类中的英雄大都是打5号位的较多,可以理解为辅助。这些英雄在对局中很少拿经济,对敌方的伤害也较低,主要提供对团队的保护作用。
2) 第四类中各个指标值都是相对较高的,通过分析其中的英雄可以发现,第四类中的英雄大都是打1号位的较多,可以理解为主力输出。这些英雄在对局中拿经济最多的经济,通常是核心输出位置。
3) 第一类中只有两个英雄,它们的特点是对英雄的伤害极高,但对建筑的伤害很低。这两个英雄为Zous和Tinker,他们的主要特点都是在队伍中扮演着强力输出以及Ganker (指负责偷袭抓人的队友)的角色,属于那种到处游走拿人头的人。所以,他们经常会对敌方英雄造成巨额伤害,却又很少进行推塔。
4) 通过分析可以看出,根据第一类的指标对英雄进行K-均值聚类的结果和实际游戏中英雄的特点是吻合的。
第二大类指标下的英雄的聚类情况如下:

Figure 6. Number of cases in each cluster
图6. 每个聚类中样本的个数
分析上图6和图7,可以得到以下结论:
1) 第一类中各个指标值都是相对较高的,通过分析其中的英雄可以发现,第一类中的英雄大都是那种版本强势的英雄。在经过游戏官方的版本更新后,这些英雄的某些属性得到提高,因此有着较高的胜率和出场率。
2) 第三类中各个指标值都是最低的,通过分析其中的英雄可以发现,第四类中的英雄都是版本弱势英雄。因此,拥有最低的KDA,胜率和出场率就是很合理的了。
3) 第四类中只有一个英雄Gudge,它的特点很明显,有着极高的出场率,而且胜率也不低。这与该英雄的特性有关:Gudge的特有神技钩子决定了他的高出场率,它最大的作用在于战场的分割与救人,对团战胜败有极高的决定作用。其次,这个技能有很强的娱乐性,适合各个级别的玩家使用。
4) 通过分析可以看出,根据第二类的指标对英雄进行K均值聚类的结果是也是符合游戏实际的。
4. 因子分析
从上文的聚类分析结果来看,所选取的9个指标存在一定的相关性,下面进行因子分析,提取影响9个指标值的公共因子,我们称为主因子。SPSS分析数据结果如下:
由上图8可以得出结论:各指标之间还是有比较大的相关性的,比如经济和正补,经济和经验。

Figure 9. KMO and Bartlett’s test
图9. KMO和Bartlett半球检验
由上图9可以得出结论:KMO的值为0.811,大于阈值0.5,所以说明了变量之间是存在相关性的,符合要求;Bartlett球形检验的结果,在这里只需要看显著性这一项,其值为0.000,小于0.05。两个结果均说明了该数据是可以进行因子分析的。本文主要采取主成分法提取公共因子。
由下图10可以得出结论:前2个主成分对变量的表达已达到了70%左右,可做为影响各指标的公共因子,完全可以用于后面相关的分析。

Figure 10. Each principal component explains the total variance of the original variable
图10. 各主成分解释原始变量总方差的情况
由上图11可以得到结论:
1) 在第一主因子F1主要由经济、经验、英雄伤害、建筑伤害、反补、正补6个指标决定。这6个指标代表了英雄在游戏中的发育情况,在游戏中英雄绝大多数的行为都与这两个系数直接相关,对敌方单位和中立单位的击杀都能够同时带来经济和经验的提高,这两个指标越高也能代表英雄在游戏中获得的资源越多;总体来说,第一主成分代表了英雄在游戏中的发育情况。
2) 在第二主因子F2主要由KDA、胜率和出场次数决定,代表了英雄的强势和弱势情况,以及玩家们对强势英雄更加热衷的状态。总体来说,第二主成分代表了英雄在游戏版本的强弱势情况。
5. 总结
1) 从描述性分析中可以得出,为保证游戏的公平性,游戏官方要保证每个英雄的胜率都差不多,维持在50%左右;也要保证每个英雄不会过于强势或劣势,所以各个英雄的KDA的方差也会很小。
2) 通过聚类分析,将英雄的9个指标划分为两个类别。第一类是游戏中英雄的发育程度相关指标。第二类是与游戏胜率有关的指标,反映了英雄的强势弱势情况。
3) 通过K均值聚类分析的结果与实际中的英雄特性的比较,分析出K均值聚类的结果是比较合理的。
4) 通过因子分析,得出两个比较具有代表性的主因子:经济和胜率。这也与之前系统聚类分析的得到的结果相是一致的。
基金项目
陆军工程大学基础学科培育基金项目(KYJBJQZL1922);陆军工程大学基础学科培育基金项目(KYJBJQZL1921)。
NOTES
* 通讯作者。