1. 引言
一直以来,对于金融方向的研究中,一个重要的课题便是对于金融时间序列波动性的研究,因为往往是波动带来风险,风险带来收益。而对于股票市场收益率波动性的研究便是对于研究金融时间序列的波动的重要手段,因为股票的波动象征着股票价格的变化,而股票价格的变化便与整个金融市场息息相关。
对于随机时间序列预测,美国学者George Box和英国统计学家Gwilym Jenkins共同建立了ARMA模型,由于利用时间序列建立的ARMA模型要求序列是平稳的,但是实际上时间序列并不可能全是表现出平稳性,就像单位根过程便是时间序列数据中的非平稳过程;于是建立了一种特殊的描述单位根过程的模型——随机游动模型,Engle于1982年提出了自回归条件异方差模型即ARCH模型,但是对于高阶ARCH效应的时候参数往往不能通过显著性检验,于是就有了广义ARCH模型,即GARCH模型 [1],而当GARCH模型不能很好地描述序列的变化的时候,为了提高精度,ARCH模型还有很多的拓展形式(EGARCH,ARCH-M,TARCH,幂ARCH,成分ARCH,非对称成分ARCH);为了研究虚拟变量对于回归模型的影响,Hamilton和Susmel建立了SWARCH模型;以此来研究加入外生变量对于股票股指的影响 [2]。
本文旨在建立一个广义的加入外生变量的GARCH模型,以此来进行对于股指变化的研究;
2. 新型广义具有外生变量的GARCH模型的建立
2.1. 多元线性回归模型——ARMA模型
ARMA模型包含两部分即AR(p)、MA(q)模型;
(1) AR(p)模型是仅用时间序列 不同滞后项作为解释变量的模型:
不同滞后项作为解释变量的模型:
 (1.1)
(1.1)
如上式, 是自回归系数;p为自回归阶数;式(1.1)便是p阶自回归模型;
是自回归系数;p为自回归阶数;式(1.1)便是p阶自回归模型;
(2) MA(q)模型仅用误差 的不同滞后项作为解释变量的模型:
的不同滞后项作为解释变量的模型:
 (1.2)
(1.2)
如上式,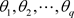 是移动平均系数;q为移动平均阶数;式(1.2)便是q阶移动平均模型 [3];
是移动平均系数;q为移动平均阶数;式(1.2)便是q阶移动平均模型 [3];
由(1) (2)可知
 (1.3)
(1.3)
令 ,
,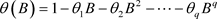 ,于是,式(1.3)便可以写成
,于是,式(1.3)便可以写成
 (1.4)
(1.4)
式(1.4)便是ARMA (p,q)模型 [1]。
2.2. 自回归条件异方差模型——GARCH模型
对于常用的回归模型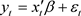 ,如果随机扰动项的平方服从AR (q)过程,即
,如果随机扰动项的平方服从AR (q)过程,即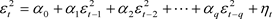 ,其中
,其中 是独立同分布的,则称上述模型为自回归条件异方差模型即ARCH模型。
是独立同分布的,则称上述模型为自回归条件异方差模型即ARCH模型。
广义ARCH模型——GARCH模型
GARCH模型被称为广义ARCH模型,是在ARCH模型基础上提出的,可以应用的范围更广,GARCH模型通常应用于对回归和自回归模型的随机扰动进行建模,GARCH (p,q)模型的表现形式如下:

2.3. 新型广义具有外生变量的GARCH模型
式(2.1)是ARMA-GARCH (p,q)模型 [4];第一个式子是ARMA均值模型,现在我们要做的是在ARMA均值模型上加入一个线性方程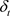 ,这个线性模型用来表示外生变量,
,这个线性模型用来表示外生变量,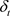 的公式是:
的公式是:
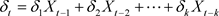 ,然后
,然后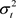 便变成了
便变成了 ,所以新型广
,所以新型广
义含有外生变量的GARCH模型的表达式如下:
 (3.1)
(3.1)
3. 数据来源与实证分析
3.1. 数据来源
本文选取的是从2013年开始到2019年的上证综指和纳斯达克综合指数的日收盘价,日收益率 的计算方法是
的计算方法是 ,其中
,其中 为日收盘价,
为日收盘价, 为滞后一日的收盘价。
为滞后一日的收盘价。
3.2. 数据描述
图1和图2分别给出纳斯达克综合指数的日收盘价和日收益率的曲线图:

Figure 1. Daily closing price of NASDAQ Composite Index
图1. 纳斯达克综合指数日收盘价

Figure 2. Daily yield of NASDAQ Composite Index
图2. 纳斯达克综合指数日收益率
图3和图4分别给出的是上证综指的日收盘价和日收益率的曲线图:

Figure 3. Daily closing price of Shanghai Composite Index
图3. 上证综合指数日收盘价

Figure 4. Daily yield of Shanghai Composite Index
图4. 上证综合指数日收益率
从图1、图2和图3、图4中我们可以发现,纳斯达克综合指数和上证综指的日收盘价是非平稳的,而经过处理后所选用的对数收益率趋于平稳,这样,我们便可以将对以收盘价的研究改为对以日收益率的研究。
4. 数据的统计检验
4.1. 收益率的正态性检验
我们以纳斯达克综合指数作为变量来研究纳斯达克综合指数和上证综指之间的关联,那么我们用EVIEWS软件测出上证综指的日收益率序列的正态性检验:

Figure 5. Normality test of daily yield series of Shanghai Composite Index
图5. 上证综指的日收益率序列的正态性检验
从图5的检验结果来看,JB值为3518.456,p值为0,检验序列的分布于正态分布无显著差异的原假设,即序列不服从于正态分布。
4.2. 平稳性检验
由图6 ADF检验结果显示,序列为平稳序列。
4.3. 序列自相关检验
图7是序列的自相关图,从图中可以看出,序列存在自相关性。
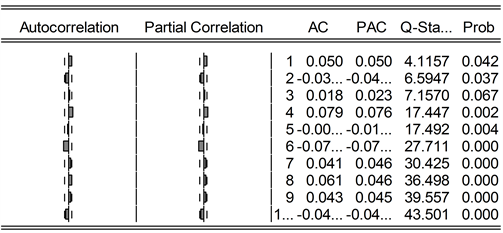
Figure 7. Autocorrelation test results of Shanghai Composite Index Series
图7. 上证综指序列的自相关检验结果
5. GARCH模型的建立
在滞后10阶的检验中,自相关和偏相关在1、4、6阶截尾,
构建ARMA (3,3)模型,如下:
从表1的回归结果来看,变量在AR (6)不显著,因此剔除,构建ARMA (1,1)模型。构建的ARMA (2,3)结果如下:
表2即为ARMA (2,3)模型,图8为模型的残差序列自相关图,即ARMA (2,3)模型不存在自相关性。
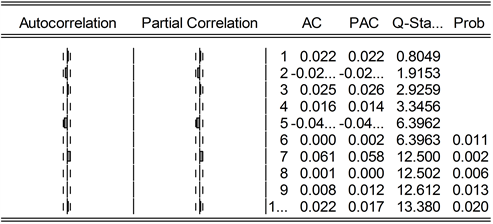
Figure 8. Auto correlation test of residual sequence of ARMA (2,3) model
图8. ARMA (2,3)模型的残差序列自相关检验
图9为ARCH_LM检验结果,说明构建的自回归模型存在ARCH效应。
如下,表3是构建的GARCH (1,1)模型结果。模型的AR根均在单位圆内,表明构建的模型是稳健的。
6. 加入X变量的GARCH模型构建
(1) X变量自相关检验
由图10可知:X在4阶和8阶存在自相关。
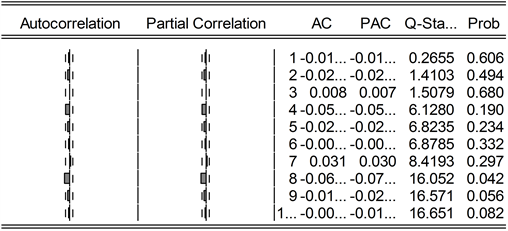
Figure 10. Auto correlation test of NASDAQ Composite Index series
图10. 纳斯达克综合指数序列的自相关检验
(2) 新的GARCH模型构建
(3) LB检验

Table 5. Coefficient equality test of X lag variable
表5. X滞后变量的系数相等检验
拒绝原假设,即系数不相等。
X滞后变量的系数相等。

Table 6. Coefficient equality test of new GARCH model
表6. new-GARCH模型系数相等检验
拒绝原假设。
r的GARCH模型系数相等。
由表4~6,由于对r的GARCH模型系数相等的检验中,我们发现实证拒绝原假设,所以得出 是
是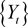 的原因,即纳斯达克综合指数的日收益率与上证综指日收益率有着密切的联系。
的原因,即纳斯达克综合指数的日收益率与上证综指日收益率有着密切的联系。
7. 结论与建议
本文主要运用了加入外生变量的GARCH模型来对上证综指和纳斯达克综合指数之间的日收益率的波动来研究两种综合指数是否具有一定的联系,实证研究表明,两种综合指数之间具有很高的契合度,所以说两种综指之间具有联系。GARCH模型中 中的
中的 是自回归模型,新型GARCH模型的建立是在
是自回归模型,新型GARCH模型的建立是在 的基础上加上一个符合自回归模型的变量,以此来组建一个新模型,根据新模型中系数是否相等来判断,变量和原量之间是否有关。
的基础上加上一个符合自回归模型的变量,以此来组建一个新模型,根据新模型中系数是否相等来判断,变量和原量之间是否有关。
本文的模型建立可以在加入一个符合自回归模型的变量的基础上改为加入含有二阶项的变量,由于本文选取的数据不符合二阶模型,所以在此提出一个想法,可以建立更好更广义的GARCH模型。