摘要:
2014年,罗马尼亚数论学家Popa通过引入素数双曲线法得到Mertens第二定理的二重推广: ∑
pq≤x1/pq=(ln(lnx)+B)
2-ln
22+∫
0+01/2ln(1-x)/x dx+(ln(lnx)/lnx),其中p,q是素数,B是Mertens常数。在本文中,我们类比Popa的方法,运用Dirichlet双曲线法在有限域上的一元多项式环中得到了Mertens第二定理的二重推广,同时类比Rosen关于代数数域中Mertens第二定理的证明方法,重新证明了有限域上的一元多项式环中的Mertens第二定理。
Abstract:
In 2014, by using the prime hyperbola method Popa developed the following double Mertens estimation: ∑pq≤x1/pq=(ln(lnx)+B)2-ln22+∫0+01/2ln(1-x)/x dx+(ln(lnx)/lnx),where p, q are prime numbers and B is Mertens constant. In this paper, by modifying the methods of Popa and based on Dirichlet’s hyperbola method, we generalize the Mertens’ second theorem to the double case on the polynomial ring over a finite field. During this approach, by modifying Rosen’s method on the proof of the Mertens’ second theorem in algebraic number field, we give a new proof of the Mertens’ second theorem on the polynomial ring over a finite field.
1. 引言
为了书写方便,在本文中 表示求和式
表示求和式 ,
, 表示求和式
表示求和式 ,其中
,其中 为
为 中
中
全体首一不可约多项式的集合。
L. Euler在1735年发表的论文中证明了下面著名的等式:
 , (1)
, (1)
其中C称为Euler-Mascheroni常数,约为0.577。
1874年,德国数学家Mertens进一步得到下面著名的Mertens定理,也叫Mertens第二定理:
 , (2)
, (2)
其中B (近似为0.261)是一个常数。该定理多次出现在本科和研究生数论教科书中,如T. Apostol [2] (详见p.90,定理4.12),G. Everest,T. Ward [3] (GTM 232,详见该书p.13),潘承彪,潘承洞 [4] (详见该书p.50)。
2014年,罗马尼亚数论学家Popa [5] 通过引入素数双曲线法,即利用如下公式:
 , (3)
, (3)
其中 是
是 上的函数,
上的函数, 。他通过对
。他通过对 进行展开,得到
进行展开,得到
如下更加精确的二重Mertens估计式:
 , (4)
, (4)
其中 是素数,B是Mertens常数。
是素数,B是Mertens常数。
Mertens第二定理除了整数环中的上述推广和改进之外,人们在有限域上的一元多项式环 中也类比得到了较好的结果。
中也类比得到了较好的结果。
1979年,南非数论学家Knopfmacher在他编写的书 [6] 中,通过引入多项式环上的范数,给出了Mertens第二定理在 中的类比:
中的类比:
定理1. 下面估计式成立
 , (5)
, (5)
其中 是
是 中的Mertens常数。
中的Mertens常数。
本文的第一个任务是类比Rosen在文 [1] 关于代数数域中Mertens第二定理的证明方法,重新证明 中的Mertens第二定理,即重新给出了上面定理1的证明。同时类比Popa在文 [5] 中的方法,运用Dirichlet双曲线法在
中的Mertens第二定理,即重新给出了上面定理1的证明。同时类比Popa在文 [5] 中的方法,运用Dirichlet双曲线法在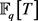 中得到了Mertens第二定理的二重推广,即下面的定理2:
中得到了Mertens第二定理的二重推广,即下面的定理2:
定理2. 下面估计式成立
 , (6)
, (6)
其中 是
是 中的Mertens常数。
中的Mertens常数。
2. 预备知识
定义1. ( [7] ) 设 ,若存在常数
,若存在常数 ,使得
,使得

成立,则称 是
是 的强函数,记为
的强函数,记为
 .
.
记 是q元有限域,
是q元有限域, 记有限域
记有限域 上的一元多项式环。
上的一元多项式环。
定义2. ( [8] ) 令 ,如果
,如果 ,则
,则 ,其中
,其中 记多项式g的次数。如果
记多项式g的次数。如果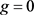 ,则
,则 。
。
下面为著名的素数定理在 中的类比。
中的类比。
引理1. ( [8],定理2.2)令 表示
表示 上的n次首一不可约多项式的个数,则
上的n次首一不可约多项式的个数,则
 .
.
下面两个引理分别是Dirichlet双曲线法和Abel求和公式。
引理2. ( [2],定理3.17) 设 为正实数且
为正实数且 ,有下式成立
,有下式成立
 ,
,
这里 。
。
引理3. ( [9] ) 设m是一个自然数, 是任意函数,
是任意函数, 是关于
是关于 的m阶和函数,即
的m阶和函数,即 。则当
。则当 时,对任意在
时,对任意在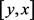 上的函数
上的函数 ,下面等式成立
,下面等式成立
 ,
,
当 时,上述引理就是Abel求和公式。
时,上述引理就是Abel求和公式。
定义3. ( [10] ) 设 为多重对数函数,定义
为多重对数函数,定义
 ,
,
 .
.
引理4. ( [10] , p.5, p.155)
(i) 对任意 ,下面等式成立
,下面等式成立
 .
.
(ii) .
.
(iii) .
.
3. 定理1的证明
为了证明我们的结论,需要下面的命题。
命题1. 下面这个估计式成立
 .
.
证明 定义
 ,
,
其中 。由引理1,可得
。由引理1,可得
 .
.
于是有
 ,
,
当t足够大时,有 和
和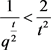 。因为
。因为 收敛,所以
收敛,所以 也收敛,且
也收敛,且 。
。
定理1的证明 记

和
 .
.
由引理3,可得
 . (7)
. (7)
由命题1,我们有
 , (8)
, (8)
其中 是有关x的有界函数,将(8)代入(7)中,我们得到
是有关x的有界函数,将(8)代入(7)中,我们得到
 .
.
通过

和
 ,
,
我们得到
 .
.
最后,记
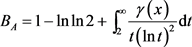 ,
,
我们就完成了这个定理的证明。
4. 定理2的证明
首先,我们需要得到 中的Mertens第一定理,即证明下面这个命题。
中的Mertens第一定理,即证明下面这个命题。
命题2. 下面估计式成立
(i)
 .
.
(ii) 当 时,我们得到
时,我们得到
 (9)
(9)
和
 . (10)
. (10)
证明 (i) 应用命题1,用 代替x,即可得到此结果。
代替x,即可得到此结果。
(ii) 令
 ,
,
应用引理3和命题1,我们得到
 .
.
对于(ii)中的第二部分,我们用 代替(9)中的x,即可得到(10)。
代替(9)中的x,即可得到(10)。
命题3. 下面估计式成立
 .
.
证明 应用下面这个公式
 , (11)
, (11)
当 时,我们得到
时,我们得到

和
 .
.
由命题2 (ii),我们知道
 , (12)
, (12)
再由符号O的性质,我们得到
 . (13)
. (13)
由公式(11),我们得到
 ,
,
显然,上式中的级数一致收敛,我们对该等式两边同时积分得
 .
.
通过引理4 (ii),我们得到
 . (14)
. (14)
特别地,把(13)和(14)代入(12)中,我们有
 .
.
定理2的证明 记
 ,
,
在引理2中,取 ,我们得到
,我们得到
 ,
,
其中

 .
.
于是有

和
 .
.
由于
 ,
,
我们得到
 .
.
于是有
 .
.
再通过命题3和定理1,我们得到
 . (15)
. (15)
因此
 .
.
这就完成了定理2的证明。