1. 引言
量子纠缠是量子信息中的重要资源，它在许多量子信息处理任务中起到了重要的作用，例如量子通信，量子隐形传态，以及量子计算的各种任务等 [1] [2] [3] [4]。正是因为这样，人们越来越关注量子纠缠的各种性质。为了量化量子的纠缠，人们提出了几种度量的方式，如冯诺依曼熵，对数负度，剩余纠缠等等。近些年来，人们已经将惯性系下的量子纠缠的研究推广到非惯性系的框架，并且在非惯性系下探究了多体量子系统的纠缠。
对于在非惯性系中的多粒子态的量子纠缠研究，人们也会利用冯诺依曼熵来研究W态量子态的纠缠演化 [5] [6] [7]。因为其他的度量方式的计算都是比较难的，而冯诺依曼熵这种度量方式的计算比较简单。如今人们也研究了非惯性系中GHZ态的纠缠变化，但是人们还没利用冯诺依曼熵来研究GHZ态的量子纠缠变化。
本文将利用冯诺依曼熵研究四体GHZ态在非惯性系下的纠缠变化。我们假设非惯性系中的观察者是处于没有任何噪声的环境中的，从而研究当1至4个观察者加速时，其纠缠的演化关系，最后通过数值分析以及图像的趋势而得到四体系统的冯诺依曼熵会随加速度的增大而增大。
2. 基本概念与知识
首先介绍冯诺依曼熵这种纠缠度量的定义，它在某些文献中也被称为部分熵纠缠度。对于一个最简单的由两个子系统A和B组成的两体纯态
，其冯诺依曼熵
可以定义为 [8] [9] [10]
(1)
其中
表示子系统A的约化密度矩阵，其数学定义可以被认为是对两体态进行部分求迹后而得到的约化密度算符
(2)
如果将约化密度矩阵
的本特征值
求出来，那么式子(1)可以写成
(3)
其中
是量子态
的本特征值。由于A和B的总体系处于纯态，利用纯态的Schmidt分解，我们可知
，从而得到A或B任何一个系统的冯诺依曼熵就是部分熵纠缠度。以上定义可以推广到N体系统。
接下来介绍Minkowski坐标系和Rindler坐标系之间的转换。在非惯性系下，Rindler坐标适合描述一类具有均匀加速的观察者，而另一个保持惯性系的观察者可以用Minkowski坐标描述。利用Alsing等提出的单模近似，可以把Minkowski空间中的费米系统真空态
写成 [11]
(4)
将单粒子激发态
写成 [11]
(5)
其中
，指数形式中的常数式子中的w，c，a分别代表Dirac粒子的频率，真空中的
光速和观察者的加速度，加速度参数r的范围是在
，其对应的加速度范围是
。而下标I和II分别代表Rindle坐标的区域一和区域二。在Rindler时空中，如果加速观察者处在I区域，那么他就不能获得II区域的信息，因此一个加速观测者是不能够获取整个时空的信息。
3. 非惯性系中四体GHZ态的纠缠
根据量子纠缠的定义，在两量子态中，相对应的最大纠缠态为Bell态，而在四量子态中，相对应的最大纠缠态为 GHZ 态，它被表示为
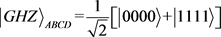(6)
其中A表示观察者Alice，B表示观察者Bob，C表示观察者Charlie，D表示观察者Daniel。
3.1. 一个观察者加速
首先考虑只有Alice观察者以加速参数r加速时，那么利用式子(4)和(5)，则式子(6)就变成
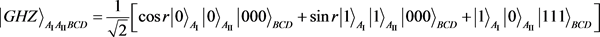
其中
和
分别表示为观察者Alice在I区域和II区域加速。由于在非惯性系里，一个加速观察者不能够获取整个时空的信息，也就是在Rindler时空中，如果加速观察者处在I区域，那么他就不能获得II区域的信息。现在我们通过对II区域求迹，就可以得到此时被四个观察者共享的量子态，如下：
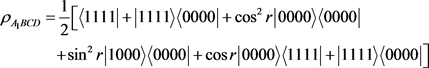
经过一些计算，我们可以得到关于
这个密度矩阵的特征值：
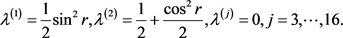
基于这些特征值，运用式子(3)，从而得到此时被四个观察者共享的量子态的冯诺依曼熵，即
从图1我们可以看出，冯诺依曼熵
随着加速参数r的增大而逐渐增加，即
与
之间的纠缠度逐渐增加。并且我们从图像可知当
时，它的最大值为0.8113。
3.2. 两个观察者有加速度
假设观察者Alice和Bob都进行加速时，利用式子(4)和(5)，那么初始GHZ态转变为
Figure 1. Curve: The 
as a function of the parameters r
图1. 冯诺依曼熵
随加速参数r变化的情况
其中
和
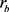分别表示为观察者Alice和Bob的加速参数。类似上面的算法，因为可以接收到的有物理意义的信息都在I区域，而II区域与观察者是无关联的。通过对II区域求迹，可以得到
接下来我们运用冯诺依曼熵来计算这个这个系统的纠缠度。第一种情况是假设观察者Alice和Bob的加速参数相同，即
，那么上面的式子就会变为
通过计算，我们可以得到它的冯诺依曼熵为
第二种情况是假设观察者Alice和Bob的加速参数不相同，即
，利用式子(4)和(5)以及经过计算可得其密度矩阵的特征值为
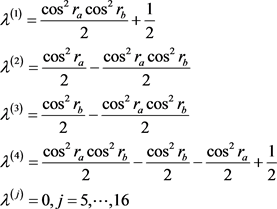
利用式子(3)，我们可得其冯诺依曼熵。第三种情况是令加速参数
取特殊值0.5。对于这三种情况，我们作出了其纠缠随加速参数变化的图像。通过图2可知，冯诺依曼熵
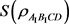随着加速参数r的增大而逐渐增加，即
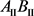与
之间的纠缠度逐渐增加。由图2的(a)和(b)可知，它们的最大值都是1.5488。在图2的(c)中，三条曲线的趋势都是一致的，当
的值一定时，其纠缠都是随着加速参数r的增大而逐渐增加。
3.3. 三个观察者加速
现在我们研究三个观察者Alice，Bob以及Charlie都有加速度，重复上面的操作，对II区域求迹，最后得
在这一小节中，我们考虑的第一种情况是观察者Alice，Bob以及Charlie的加速参数相同，即
，那么上面的式子可以写为
经过计算，我们所得的特征值为
我们考虑的第二种情况是观察者Alice和Bob的加速参数相同，而与观察者Charlie的加速参数不同，即
，经过类似的计算，我们也计算出这个情况的特征值，如下
除此之外，我们还会考虑第三种特殊情况，令观察者Alice的加速参数取定值，即
。由于这三种情况的冯诺依曼熵的表达式太冗长，所以没有写出来。对于这三种情况，我们作出了其纠缠随加速参数变化的图像。通过图3可知，冯诺依曼熵
随着加速参数r的增大而逐渐增加，即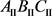
与
之间的纠缠度逐渐增加。由图3的(a)和(b)可知，它们的最大值都是2.2169。在图3的(c)中，当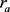
的值一定时，它的最大值是2.0086。
3.4. 四个观察者都有加速度
最后，我们将研究所有观察者都有相同的加速度的情况。对所有II区域求迹后，得到I区域中的约化密度算符为
同理，我们能算出其特征值和冯诺依曼熵。我们作出了其纠缠随加速参数变化的演化图象。通过图4可知，很明显地，我们可以看出，冯诺依曼熵
随着加速参数r的增大而逐渐增加，即
与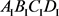
之间的纠缠度逐渐增加。并且我们从图象可知当
时，它的最大值为2.6714。
Figure 4. Curve: the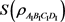 
as a function of the parameters r
图4. 冯诺依曼熵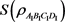
随加速参数r变化的情况
4. 总结
本文利用冯诺依曼熵研究非惯性系下四体GHZ态的纠缠演化。本文假设非惯性系中的观察者是处于没有任何噪声的环境中，从而研究了当1至4个观察者加速时，其纠缠的演化关系。主要是先假设观察者加速的数量，再根据Rinder坐标，利用对II区的求迹得到系统的密度矩阵，最后利用冯诺依曼熵这种度量的公式，从而通过数值分析以及图像的趋势得到四体系统的冯诺依曼熵会随加速度的增大而增大，
同时也求出当
时，其所得到的最大值。