1. 引言
随着全球定位系统的发展,基于位置服务 [1] (LBS, location based services)的应用越来越广泛,人们通过这些应用可以发现最近的酒店、超市和医院等,它们正在改变着信息时代人们的生活 [2] [3]。LBS服务过程中会产生大量包含用户的会见、位置信息的数据。人们可以通过对这些数据进行分析、挖掘,得到大量可用信息以帮助决策者实施相关政策,例如通过分析某个区域内用户的轨迹信息,可以发现用户曾经或者未来感兴趣的位置,在这些位置建立相应的商场,广场等,帮助投资者实现盈利的最大化。然而,分析这些轨迹数据,也可以推断出用户的一些日常轨迹、身体情况等隐私信息,如果这些个人隐私信息被泄露,会对用户造成极大的威胁 [4] [5] [6] [7] [8]。因此对用户轨迹隐私信息保护技术的研究,已经成为信息安全领域研究的重要内容之一。
在轨迹数据隐私保护过程中,轨迹的相似性是轨迹聚类和匿名化的重要因素。然而,如果匿名集合内的k条轨迹的太过相近,即它们在很长一段时间内经过同一个敏感区域,或者完全重合,那么也会泄露轨迹隐私信息的情况。文献 [7] 提出构建的轨迹k-匿名集和要具有一定的差异性,以此来降低轨迹隐私信息泄露的风险,它通过采用最小边界矩形MBR (Minimum Bounding Rectangle)大于一个给定阈值的方式来保证轨迹间的差异性。文献 [8] 首次用轨迹间夹角和距离构造轨迹图的边权的方法,文献 [9] 又在其基础之上设计了一种基于图划分的个性化隐私保护方法,利用轨迹距离和轨迹夹角度量来构造轨迹间边权,将构建轨迹k-匿名集和转化为轨迹k-子图的划分问题。Abul等人 [10] 提出NWA (never walk alone)方法,该方法提出了一个基于共定位的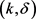 -匿名模型,首相将轨迹集合划分为互不相交的子集,其次利用聚类算法形成轨迹k-匿名集合;Cai等人 [11] 提出了一种以用户为中心的轨迹隐私保护方法以防止轨迹攻击。他们引入位置语义多样性以最大化轨迹隐私,攻击和防御问题被转化为贝叶斯Stackelberg方式以进行定量分析。对轨迹发布数据的隐私保护研究领域,已有大量学者进行了研究 [12] [13] [14]。
-匿名模型,首相将轨迹集合划分为互不相交的子集,其次利用聚类算法形成轨迹k-匿名集合;Cai等人 [11] 提出了一种以用户为中心的轨迹隐私保护方法以防止轨迹攻击。他们引入位置语义多样性以最大化轨迹隐私,攻击和防御问题被转化为贝叶斯Stackelberg方式以进行定量分析。对轨迹发布数据的隐私保护研究领域,已有大量学者进行了研究 [12] [13] [14]。
这些隐私保护方法一定程度保护了轨迹隐私,但是均未考虑轨迹因相似而泄露轨迹信息的情况,另外,在轨迹聚类中心的选取上较为不合理,因此本文提出了基于k-means++的轨迹 -匿名算法。本文有两个贡献,第一优化了轨迹聚类中心的选择,第二将轨迹斜率作为敏感属性,用
-匿名算法。本文有两个贡献,第一优化了轨迹聚类中心的选择,第二将轨迹斜率作为敏感属性,用 约束轨迹相似度以解决轨迹相似性攻击问题。
约束轨迹相似度以解决轨迹相似性攻击问题。
2. 相关概念
定义1 轨迹,移动对象O的轨迹T为三维时空坐标拟合的曲线,表示为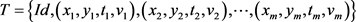 ,其中Id为移动对象的身份标识;
,其中Id为移动对象的身份标识;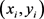 为O在i时刻的位置坐标并且
为O在i时刻的位置坐标并且 ;
; 是在
是在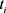 时刻的速度。
时刻的速度。
定义2 [14] 同步轨迹。两条不同的轨迹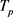 和
和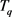 ,如果轨迹
,如果轨迹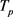 和
和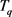 具有相同的时间序列,那么我们称
具有相同的时间序列,那么我们称 和
和 是同步轨迹;如果轨迹集合中的任意两条轨迹两两同步,则称轨迹集合是同步的。
是同步轨迹;如果轨迹集合中的任意两条轨迹两两同步,则称轨迹集合是同步的。
然而,在我们实际环境中移动对象的轨迹往往不是同步的。主要有两个原因:一是由于移动终端或GPS对每个移动对象位置的采样时间不同;二是由于不同移动对象向位置服务器(LBS)发送请求服务的时间各不相同。另外,本文在做轨迹处理时,我们假设轨迹在2个样本时间点内匀速直线运动,对于轨迹 和
和 间不同时间坐标,通过在轨迹中插入相应时刻的位置坐标来实现轨迹
间不同时间坐标,通过在轨迹中插入相应时刻的位置坐标来实现轨迹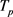 和
和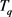 的同步。
的同步。
定义3 轨迹等价类。若轨迹 满足1)
满足1) 的起始时间
的起始时间 ,并且终止时间
,并且终止时间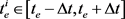 ;2)任意轨迹
;2)任意轨迹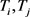 是同步的,那么轨迹
是同步的,那么轨迹 是一个轨迹等价类。
是一个轨迹等价类。
定义4 Fréchet距离 [15]。设二元组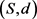 是一个度量空间,其中d是S上的度量函数。在单位区间[0,1]上的映射
是一个度量空间,其中d是S上的度量函数。在单位区间[0,1]上的映射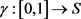 是连续映射,则称γ为S上的连续曲线。从单位区间到其自身的映射
是连续映射,则称γ为S上的连续曲线。从单位区间到其自身的映射 ,满足如下三个条件:1) ζ是连续的;2) ζ是非降的,即对于任意
,满足如下三个条件:1) ζ是连续的;2) ζ是非降的,即对于任意 ,且
,且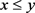 ,都有
,都有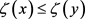 成立;3) ζ是满射,则称函数ζ为单位区间[0,1]的重参数化函数,且此时有
成立;3) ζ是满射,则称函数ζ为单位区间[0,1]的重参数化函数,且此时有 。特别地,当ζ为恒等函数
。特别地,当ζ为恒等函数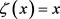 时,称ζ为平凡重参数化函数,否则,称ζ为非平凡重参数化函数。显然单位区间的重参数化函数有无穷多个。
时,称ζ为平凡重参数化函数,否则,称ζ为非平凡重参数化函数。显然单位区间的重参数化函数有无穷多个。
设A和B是S上的两条连续曲线,即 。又设
。又设 和
和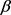 是单位区间的两个重参数化函数,即
是单位区间的两个重参数化函数,即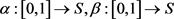 。则曲线A和B的Fréchet距离
。则曲线A和B的Fréchet距离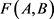 定义为
定义为
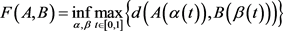 (1)
(1)
其中d是S上的度量函数。
定义5 离散Fréchet距离 [15]。设 是一个折线段曲线,我们用
是一个折线段曲线,我们用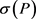 表示每个折线段的终点,即
表示每个折线段的终点,即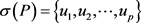 ,那么曲线P和Q的一个组合序列
,那么曲线P和Q的一个组合序列 ,且每个序列对都不相同,并且
,且每个序列对都不相同,并且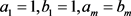 ,对任意i,有
,对任意i,有 和
和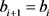 或
或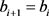 ,因此组合序列对必须遵循曲线P和Q所有点的顺序,定义L的长度为所有序列对的最大距离,即
,因此组合序列对必须遵循曲线P和Q所有点的顺序,定义L的长度为所有序列对的最大距离,即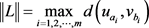 。那么折线段P和Q的离散Fréchet距离为:
。那么折线段P和Q的离散Fréchet距离为:
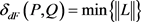 (2)
(2)
定义6 轨迹之间的曼哈顿距离。任意两条轨迹 和
和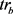 之间的曼哈顿为轨迹上所有位置点曼哈顿距离之和的平均值,定义为:
之间的曼哈顿为轨迹上所有位置点曼哈顿距离之和的平均值,定义为:
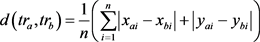 (3)
(3)
定义7  -约束。轨迹匿名集合
-约束。轨迹匿名集合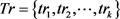 满足
满足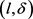 -约束,当且仅当轨迹匿名集合
-约束,当且仅当轨迹匿名集合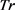 中至少有l个不同斜率的轨迹,并且轨迹间斜率差异值至少为δ。
中至少有l个不同斜率的轨迹,并且轨迹间斜率差异值至少为δ。
定义8  -匿名模型。匿名集合
-匿名模型。匿名集合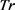 中至少有k个轨迹,并且这些轨迹满足
中至少有k个轨迹,并且这些轨迹满足 -约束。
-约束。
定义9 轨迹相似性攻击。一个匿名集合中如果存在多条高度相似的轨迹,尤其是运行轨迹相近或者平行亦或者重复,那么攻击者可以对这些发布的轨迹数据进行推理就能获得这些轨迹的大致运动轨迹及其敏感信息,若发布的轨迹均经过同一敏感区域,攻击者可以推断出该集合内的所有轨迹均有很大概率经过该敏感区域,用户隐私也随之暴露,这种攻击模式我们称之为轨迹相似性攻击。
定义10 轨迹斜率。轨迹数据的起始点、中间点和终止点所在线段的平均斜率。若采样轨迹片段Tr在起始时刻时位置为 ,中间时刻位置为
,中间时刻位置为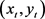 ,结束时刻位置为
,结束时刻位置为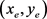 ,则该轨迹斜率
,则该轨迹斜率 为:
为:
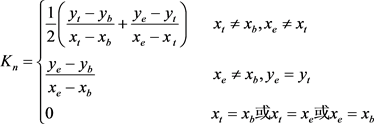 (4)
(4)
3. 基于k-means++抗相似性攻击的轨迹匿名算法
3.1. 轨迹预处理
轨迹预处理过程有以下两个步骤,首先,我们选取具有相同开始时间和结束时间的轨迹构造轨迹等价类;针对实际环境中的移动对象同时开始并且同时结束的数量非常少,文献 [9] 采用轨迹集合中的最大开始时间和最小结束时间作为构造轨迹等价类的约束条件。这种方式存在的问题是如果轨迹的开始时间或者结束时间相差很大,构建轨迹集合时就会损失很多轨迹信息,同时在形成匿名集合时也会造成很大的信息损失。鉴于此,本文选取一个给定时间间隔内的轨迹以保证轨迹间的高相似性;其次,将第一步已经选取的轨迹通过轨迹同步化形成轨迹等价类。
例如,设轨迹的起始时间为7:00,终止时间为8:00,时间间隔为5分钟,那么选取轨迹开始时间在[6:55, 7:05],结束时间在[7:55, 8:05]的所有轨迹,并将这些轨迹进行同步化,最终形成一个轨迹等价类。对于间隔时间 的选择,主要依据轨迹采样时间的稀疏程度,如果采样时间稀疏,那么间隔时间
的选择,主要依据轨迹采样时间的稀疏程度,如果采样时间稀疏,那么间隔时间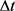 可以相对大一点;如果采样时间点密集,则间隔时间
可以相对大一点;如果采样时间点密集,则间隔时间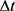 相应选取小一点。
相应选取小一点。
算法1 预处理算法 (Pre-process)
输入:原始轨迹集合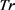
输出:轨迹等价类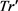
(1) for tr in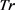 :
:
(2) If 轨迹的开始、结束时间在给定范围内那么
(3) 将tr添加到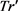 中
中
(4) for each 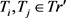
(5) for 
(6) If  and
and 
(7) 将 时间点插入
时间点插入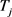 中
中
(8) else 将 时间点插入
时间点插入 中
中
(9) 返回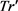
3.2. 构建轨迹匿名集合
目前大部分轨迹隐私保护算法构建匿名集合时在选择聚类中心主要通过随机选取k个匿名中心,随后构建匿名集合,这样的作法会导致轨迹匿名中心的选取不合理以至构建的匿名集合信息损失大,轨迹可用性降低,本文采用k-means++算法构建匿名集合,解决了上诉问题。
算法2 基于k-means++的轨迹匿名算法
输入:预处理之后的轨迹等价类
输出:轨迹匿名集合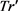
(1) 随机选取一个轨迹作为第一个聚类中心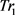
(2) 计算每个样本与当前已有类聚中心最短距离(即与最近一个聚类中心的距离),用D(x)表示;这个值越大,越可能成为轨迹的聚类中心
(3) 重复步骤二,直到选出k个聚类中心;
(4) 针对轨迹等价类中每个轨迹 ,计算它到k个聚类中心的距离并计算距离最小的聚类中心所对应的类中斜率差值是否满足
,计算它到k个聚类中心的距离并计算距离最小的聚类中心所对应的类中斜率差值是否满足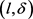 约束,如果满足加入所在类,否则计算次近的类,以此类推;
约束,如果满足加入所在类,否则计算次近的类,以此类推;
(5) 针对每个匿名集合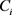 ,重新计算聚类中心
,重新计算聚类中心 (即该匿名集合的质心);
(即该匿名集合的质心);
(6) 重复(4),(5)直到聚类中心不在变化。
4. 轨迹隐私水平和数据可用性
本文主要从两个方面分析算法的可行性,一是k-匿名的隐私保护程度即泄密风险,第二,分析轨迹数据的信息损失率即数据的可用性。
4.1. 隐私保护水平
隐私保护水平的评估主要评估匿名集合中轨迹被重新识别的概率,即由构建的匿名集合推断出原使集合记录的可能性,一般采用用匿名集合与原轨迹集合同一记录的相关程度来衡量。
定义11链接成功。匿名集合内任一轨迹记录t,计算t到原始集合中所有轨迹记录的距离,得到距离t最近的记录集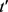 ,次近记录集
,次近记录集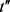 ,如果
,如果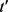 或
或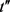 是由t匿名化得到的,则称t链接成功。
是由t匿名化得到的,则称t链接成功。
基于距离的评估思想为:用匿名集合链接成功的记录所占比例大小作为泄密风险的测量,设link_records为匿名集合链接成功的记录数,total_records为总记录数,则泄密风险值LR为:
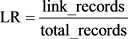 (5)
(5)
4.2. 信息损失率
我们在计算信息损失率时,仅仅考虑构建轨迹匿名集合时造成的信息损失,不考虑轨迹预处理的信息损失。本文通过轨迹的匿名区域与整个轨迹空间区域的面积的比值来衡量信息损失,轨迹匿名区域与数据可用性成反比,匿名区域面积越大数据可用性越小,反之数据可用性越大,表示为:
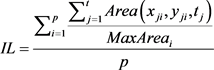 (6)
(6)
其中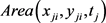 表示
表示 时刻的匿名区域面积,
时刻的匿名区域面积,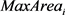 表示第i个匿名集合的最大面积,p表示匿名集合的个数。
表示第i个匿名集合的最大面积,p表示匿名集合的个数。
5. 实验结果与分析
5.1. 实验环境和数据
我们的实验环境为Inte(R) Core(TM) i5-4590 CPU @3.30 GHz;8 G内存;Microsoft Windows 7.sp。64位操作系统;本算法在pycharm中实现。实验中使用的实验数据集是由Brinkhoff生成器基于德国奥尔登堡市交通地图生成的 [16],初始数据集如表1所示。第一列表示移动对象的编号,第二列是移动对象位置编号即表示该点是轨迹的第几个位置,第三列表示数据返回的概率,0表示以百分百的概率生成数据点,第四列表示轨迹所处的时间;第五、六列表示轨迹所处的位置信息,第七列表示轨迹的当前速度;最后两列表示轨迹下一时刻将要到达的位置。
5.2. 隐私保护水平
通过图1可以看出基于k-means++的轨迹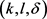 -匿名算法相比CMPT,NWL两种匿名算法泄密风险小很多。基于k-means++算法构建的轨迹匿名集合更为合理,轨迹间的距离相比其它算法会小一点;另外,由于
-匿名算法相比CMPT,NWL两种匿名算法泄密风险小很多。基于k-means++算法构建的轨迹匿名集合更为合理,轨迹间的距离相比其它算法会小一点;另外,由于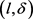 的约束,每个等价类在聚类时要求类内至少有l个轨迹斜率差异值至少为
的约束,每个等价类在聚类时要求类内至少有l个轨迹斜率差异值至少为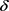 ,避免了匿名集合间轨迹的过度相似,能够有效抵制轨迹相似性攻击,防止隐私泄露。
,避免了匿名集合间轨迹的过度相似,能够有效抵制轨迹相似性攻击,防止隐私泄露。

Figure 1. Different methods of disclosure risk
图1. 不同方法的泄密风险
由图2可知,基于k-means++的轨迹 -匿名算法在取不同k值时,随着
-匿名算法在取不同k值时,随着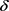 值的增加可以获得更安全的匿名数据,大大减少了信息泄露的可能性。以上实验结果表明,本文算法具有一定的可用性。
值的增加可以获得更安全的匿名数据,大大减少了信息泄露的可能性。以上实验结果表明,本文算法具有一定的可用性。

Figure 2. Different delta value changes correspond to the leak risk
图2. 不同δ值变化对应的泄密风险
5.3. 轨迹信息损失
图3是CMPT,NWL匿名算法与基于k-means++的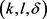 -匿名算法信息损失随着k值的变化的情况。基于k-means++的
-匿名算法信息损失随着k值的变化的情况。基于k-means++的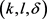 -匿名算法略微比其它两种算法的信息损失度低,这是由于尽管聚类时要保证轨迹间至少有l个斜率差异值至少为
-匿名算法略微比其它两种算法的信息损失度低,这是由于尽管聚类时要保证轨迹间至少有l个斜率差异值至少为 ,但是,本文采用k-means++算法构建轨迹匿名集合相比于传统的聚类算法构建的匿名集合更为合理,轨迹间的距离更小,因此本文算法信息损失略低。
,但是,本文采用k-means++算法构建轨迹匿名集合相比于传统的聚类算法构建的匿名集合更为合理,轨迹间的距离更小,因此本文算法信息损失略低。
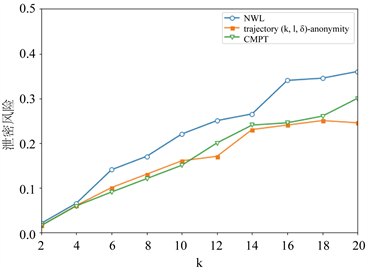
Figure 3. Information loss of different methods
图3. 不同方法的信息损失
由图4可见,基于k-means++的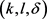 -匿名算法随斜率差异值
-匿名算法随斜率差异值 的增大,取不同k值时信息损失度均增大。随着
的增大,取不同k值时信息损失度均增大。随着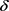 增大,类内轨迹斜率取值差异增大,导致类内轨迹距离增大,从而增加了信息损失量。
增大,类内轨迹斜率取值差异增大,导致类内轨迹距离增大,从而增加了信息损失量。
5.4. 算法运行时间分析
图5是本文算法与其它两种匿名算法的运行时间比较。由于本文匿名算法要求在构建轨迹等价类时,满足k-匿名的条件下同时满足至少有l个轨迹斜率差异值至少为e的轨迹,所以本文算法在k取值增加的情况下,运行时间会略微增加,但可忽略不计。
Figure 4. Information loss of different k values with delta change
图4. 不同k值随δ变化的信息损失

Figure 5. Running time of different methods
图5. 不同方法的运行时间
6. 总结
本文提出的基于k-means++的轨迹 -匿名算法解决了聚类中心的选取问题以及因轨迹间的相似性过高导致泄露轨迹隐私泄的问题。相比其它轨迹k-匿名算法,本文将轨迹斜率作为轨迹的敏感属性,优化了聚类中心的选择,以及增加了等价类内轨迹
-匿名算法解决了聚类中心的选取问题以及因轨迹间的相似性过高导致泄露轨迹隐私泄的问题。相比其它轨迹k-匿名算法,本文将轨迹斜率作为轨迹的敏感属性,优化了聚类中心的选择,以及增加了等价类内轨迹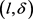 -约束,即要求匿名集在满足轨迹k-匿名的同时还需满足至少有l个斜率差异值至少为
-约束,即要求匿名集在满足轨迹k-匿名的同时还需满足至少有l个斜率差异值至少为 ,避免了因出现大量相似甚至于平行的轨迹而导致隐私的直接泄露的问题。实验结果表明本文算法得到的匿名算法在抵抗轨迹相似性攻击的能力方面更强,并且也保证了轨迹数据的可用性。
,避免了因出现大量相似甚至于平行的轨迹而导致隐私的直接泄露的问题。实验结果表明本文算法得到的匿名算法在抵抗轨迹相似性攻击的能力方面更强,并且也保证了轨迹数据的可用性。