1. 引言及主要结果
本文使用值分布论的基础知识及Nevanlinna常用理论的标准符号 [1] [2] [3],设
与
为复平面上的两个非常数亚纯函数,而a为扩充复平面中的元素,若
,则称a为亚纯函数
与
的IM分担值;若a为亚纯函数
与
的IM分担值,且对于
都有
作为方程
的根的重数与
作为方程
的根的重数相同,则称a为亚纯函数
与
的CM分担值。
对于复平面上的非常数亚纯函数
而言,
泛指形如
的量。
1929年,Nevanlinna证明了以下定理:
定理A [1] 若非常数亚纯函数
与
具有5个判别的IM分担值,则
。
定理B [1] 若非常数亚纯函数
与
以4个两两判别的复数
为CM分担值,则以下情况之一必发生:
(i)
;
(ii)
,但
是
的分式线性变换,且
中必有两个是
与
公共的Picard例外值。
1979年,G. G. Gundersen得到了
定理。
定理C [2] 设
为4个判别的复数,如果非常数亚纯函数
与
以
为CM分担值,而以
为IM分担值,则
均为
与
的CM分担值。
1983年,Gundersen将定理C改进为如下的
定理。
定理D [3] 设
为4个判别的复数,如果非常数亚纯函数
与
以
为CM分担值,而以
为IM分担值,则
亦为
与
的CM分担值。
Gundersen根据上述结果,提出了以下公开问题:
设
为4个判别的复数。如果
为非常数亚纯函数
与
的IM分担值,
为
与
的CM分担值,那么
是否一定亦都为
与
的CM分担值?
对于上述问题,1992年,Gundersen得到如下的阶段性结果。
定理E [4] 设c为异于
的复数,
与
为判别的非常数亚纯函数。如果
与
以
为IM分担值,而以
为CM分担值,且
及
使
以及
,则
均为
与
的CM分担值。
对于Gundersen的上述问题,在本文中我们得到如下几个结果。
定理1.1 设
与
为判别的非常数亚纯函数。如果
与
以
为IM分担值、而以
为CM分担值,且
及
使得
以及对
都有
,
,
则
均为
与
的CM分担值。
定理1.2 设
与
为判别的非常数亚纯函数。如果
与
以
为IM分担值、而以
为CM分担值,且
及
使得
以及对
都有
,
,
则
都为
与
的CM分担值。
2. 几个引理
为了证明本文的结果,我们需要以下几个辅助结果。
引理2.1 [1] 设
为非常数亚纯函数
与
的四个判别的IM分担值。如果
,那么:
(i)
,
;
(ii)
,
;
(iii)
;
(iv)
;
其中
表示
的零点,但不是
的零点的计数函数,
类似定义,
表示
与
重级均大于1的公共零点的计数函数,按重级小者计算次数。
引理2.2 [1] 设c为有穷复数,且
,非常数亚纯函数
与
以
及c中的任何一个为IM分担值,令
,
,
,
则有
,
,
,
其中
表示
与
公共的单重零点的密指量,
,
亦类似定义。
引理2.3 [1] 设常数
,如果判别的非常数亚纯函数
与
以
及c的每一个值为IM分担值,
,而
如引理2.2中所述,令
,
,
,又设
是
与
公共的单重极点,则
,
,
。
3. 定理1.1的证明
令
,
,
,
,
,
则
为整函数,又由对数导数引理知
,故
。由于
为
与
的CM分担值,且由引理2.1 (iv)知
. (1)
由(1)式及引理2.2知
, (2)
, (3)
.(4)
我们断言
。
事实上,若
,由Nevanlinna第一基本定理及(2)~(4)式得
.
由上式可得
.
又由引理2.1 (iii)得
. (5)
继令
.
若
为f与g的极点,则
为
的零点。由引理2.1 (iv)及已知条件可知
. (6)
结合(5)式可知
.
这与定理的假设
及
使得
,且
矛盾,所以断言成立。故
。
不失一般性,令
即
,设
. (7)
由(7)式可知
,故有
。又因
为一个整函数,故0和
为P的Picard例外值。
因而有
. (8)
(其中
为一个整函数)。由(8)式可知:0和
为
与
公共的CM分担值,且结合
为
与 公共的IM分担值与定理D可知
公共的IM分担值与定理D可知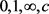 均为
均为 与
与 的CM分担值。定理1.1证毕。
的CM分担值。定理1.1证毕。
4. 定理1.2的证明
若 ,令
,令
 .
.
我们断言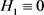 。事实上,若
。事实上,若 ,则由Nevanlinna第一基本定理及引理2.2可知
,则由Nevanlinna第一基本定理及引理2.2可知
 ,
,
由上可得
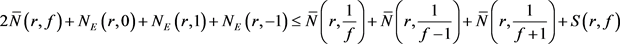 . (9)
. (9)
由引理2.1 (iv)可知
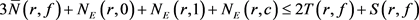 .
.
再结合定理1.2的已知条件及定理1.1中的(6)式可知
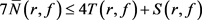
这与定理的假设 及
及 使得
使得 ,且
,且
 矛盾,所以断言成立。故
矛盾,所以断言成立。故 。
。
若 时,即
时,即
 . (10)
. (10)
由(10)式经积分可以得到
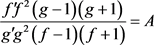
(其中A为非零常数)。再结合 为
为 与
与 公共的IM分担值可知:
公共的IM分担值可知: 均为
均为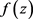 与
与 的CM分担值。
的CM分担值。
若 ,令
,令
 ,
, .
.
我们有 ,故
,故 。又因
。又因 为一个整函数,故0和
为一个整函数,故0和 为
为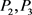 的Picard例外值,即
的Picard例外值,即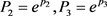 (其中
(其中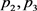 为一个整函数),由此可知0和
为一个整函数),由此可知0和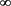 为
为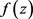 与
与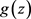 公共的CM分担值,且结合
公共的CM分担值,且结合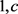 为
为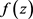 与
与 公共的IM分担值与定理D可知:
公共的IM分担值与定理D可知: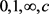 均为
均为 与
与 的CM分担值。
的CM分担值。
同理,若 ,令
,令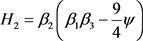 ;若
;若 ,令
,令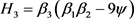 。与上面类似的过程可证
。与上面类似的过程可证
得定理1.2的结论。
参考文献