基于随机波动率的LNG远期定价模型

LNG Forward Pricing Model Based on Stochastic Volatility

摘要: 本文考虑液化天然气(LNG)远期价格的随机波动率因素，采用等价鞅测度和伊藤公式得到波动率过程，利用矩估计法对模型中的参数进行估计，建立了随机波动率的远期定价模型。实证分析表明，加入随机波动率因素的定价机制优势更明显。

Abstract: This paper considers the stochastic volatility factor of the LNG forward price, uses the equivalent martingale measure and the Ito formula to obtain the volatility process, and uses the moment es-timation method to estimate the parameters in the model. Empirical analysis shows that the ad-vantages of the pricing mechanism with stochastic volatility factors are more obvious.

1. 引言

2019年10月14日，美国芝加哥商业交易所推出首份可以进行实物交割的LNG期货合约 [1]，进一步促进了天然气产业的发展，有利于形成全球统一的市场基准价格。自页岩气大规模开发以来，美国从全球最大的天然气进口国之一，于2017年成为天然气净出口国，这意味着美国很可能在未来LNG定价方面掌握更多的主动权。研究表明，我国是全球最大的天然气进口国，预计到2024年，中国的LNG进口量将超过日本成为全球最大的LNG进口国 [2]。因此，研究复杂市场环境下的LNG定价机制，对我国天然气市场的完善和发展具有理论价值和现实意义。

目前，国内外已有学者对天然气价格进行研究。高志远 [3] 构建能源价格可计算一般均衡(Computable General Equilibrium, CGE)模型对宏观经济变量进行模拟分析，并针对能源价格对国民经济的影响进行政策模拟。赫永达等 [4] 通过构建非完全竞争的CGE模型，模拟了在不同情景下国际天然气价格波动对居民生活及产业结构的影响，认为国际天然气价格波动对中国经济的影响将越来越大，天然气价格波动的风险不容忽视。薛凤，黄圣明 [5] 利用VAR模型和脉冲响应函数研究了我国天然气价格波动的原因，结果表明天然气价格与国民生产总值、电价等有着交互的正向影响，为天然气价格改革相关政策的指定提供了一定的理论依据。苏鹏 [6] 等人通过构建静态CGE模型模拟天然气价格变动对宏观经济各部门及出口和消费的影响，指出天然气价格上涨对宏观经济各变量影响较小，但是会显著影响我国天然气产量和相关产品的进出口。Brigida M [7] 在对天然气和原油定价模型进行计算时，在满足马尔科夫条件下协整方程的m个状态之间可以互相转换，精确计算后得到天然气和石油价格之间的协整关系。邢文婷 [8] 等人考虑了季节性和跳跃性因素建立了天然气期货定价模型。马超群 [9] 等人在GSC模型 [10] 的基础上，同时考虑石油与天然气的协整关系与收益率的不确定性，提出了多资产大宗商品远期定价模型(GSCR模型)。

在资产定价模型的研究中，资产价格的波动率是一个非常重要的参数。在各类衍生证券定价问题中，传统确定波动率的做法是隐含波动率法，即Black-Scholes公式得到的期权价格与市场价相等时的波动率取值，因此波动率取值为固定的常数。然而，很多学者对波动率为常数的假设持怀疑态度，实证数据表明隐含波动率与行权价格之间呈现出“波动率微笑”特征，且金融市场中标的资产价格具有“尖峰厚尾”现象 [11]。为了弥补常数波动率模型的不足，学者们开始研究随机波动率模型。吴育鑫 [12] 提出了随机波动率下的期权定价模型，并通过实证表明随机波动率模型比传统的常数波动率模型更加精确。李亚茹 [13] 等运用随机波动率Heston模型对农产品期货价格保险进行定价。但这些模型都假设标的资产的利率和便利收益为常数。

大宗商品与普遍意义的资产不同，生产量与消费量不需要严格匹配，持有者在持有大宗商品时会产生便利收益，且标的资产的收益具有不确定性。众多学者研究大宗商品定价时均采用均值回复过程刻画便利收益和收益率。Schwartz [14] [15] 在便利收益和随即利率服从均值回复的假设下，建立了三因子模型。本文在三因子模型的基础上，考虑加入随机波动率对天然气远期进行定价，以期获得合理有效的定价效果。

2. 天然气远期价格定价模型

2.1. 随机波动率的确定模型

假设市场不确定性由概率空间 $\left(\Omega ,F,Q\right)$ 表示， $\Omega$ 为样本空间，F为 $\sigma$ 代数，Q代表测度。t时刻资产的价格为 $S_t$，其便利收益为 ${\delta }_t$，收益率为 $r_t$，标的资产价格、便利收益和收益率三者间具有相关性， $v_t$ 表示随机波动率过程。考虑标的资产波动率的不确定性性，在随机波动率模型的基础上提出如下标的资产价格模型：

$\text{d}{S}_t=\left(\mu +r_t-{\delta }_t\right)S_t\text{d}t+\sqrt{v_t}{S}_t\text{d}{W}_{S,t}$ (1)

$\text{d}{r}_t=k_r\left(m-r_t\right)\text{d}t+{\sigma }_r\text{d}{W}_{r,t}$ (2)

$\text{d}{\delta }_t=k_{\delta }\left(\alpha -{\delta }_t\right)\text{d}t+{\sigma }_{\delta }\text{d}{W}_{\delta ,t}$ (3)

$\text{d}{v}_t=k_v\left(\theta -v_t\right)\text{d}t+{\sigma }_v\sqrt{v_t}\text{d}{W}_{v,t}$ (4)

式中， $\mu$ 表示标的资产价格的平均增长率， $k_r$ 、 $k_{\delta }$ 和 $k_v$ 分别表示收益率、便利收益和随机波动率过程的均值回复速率，m、 $\alpha$ 和 $\theta$ 分别表示收益率、便利收益和随机波动率过程的均值回复水平， ${\sigma }_r$ 、 ${\sigma }_{\delta }$ 和 ${\sigma }_v$ 分别表示收益率、便利收益和随机波动率过程的波动率系数， $\text{d}t$ 为时间间隔， $\text{d}{W}_s$ 、 $\text{d}{W}_r$ 、 $\text{d}{W}_{\delta }$ 和 $\text{d}{W}_v$ 均表示服从布朗运动。

2.2. 随机波动率模型的参数估计

典型非线性、非高斯状态空间随机波动率模型的似然函数是及其复杂的高维积分，难以得到精确似然函数，因此采用条件矩估计法 [16] 估计参数。然而波动率是不可观察的，我们必须通过标的资产价格适当构造波动率的样本，再利用方程(4)得到模型参数的估计。

设 $S_0,S_1,\cdots ,S_{n-1}$ 是标的资产价格 $S_t$ 在 $\left[0,T\right]$ 时段内的观察值，其中 $S_t$ 对应 $t_i=\frac{iT}{n}$ 时刻的观察值。

根据 $\mu$ 的市场意义，它表示标的资产价格的平均增长率，即

$\mu =E\left(\frac{S_t-S_j}{S_j\left(t-j\right)}\right)$

因此，构造 $\mu$ 的矩估计量为

$\hat{\mu }=\frac{\text{1}}{n}{\displaystyle \underset{t=0}{\overset{n=1}{\sum }}\left(\frac{S_{t+1}-S_t}{S_t\left(t_{t+1}-t_t\right)}\right)}$

接下来构造随机波动率过程 $v_t$ 的样本。需先消去漂移项 $\mu +r_t-{\delta }_t$，利用Ito公式，通过对过程 $\left\{S_t,t\ge 0\right\}$ 的变换，构造 $\sqrt{v_t}{S}_t$ 的样本。以 $F_t$ 表示由 $\left\{W_s,0\le s\le t\right\}$ 生成的 $\sigma$ 域，Q表示由过程 $W_t$ 在 $F_t$ 上导出的测度，令

$W_{S,t}^{\ast }=W_{S,t}+{\displaystyle {\int }_0^t\frac{\mu +r_t-{\delta }_t}{\sqrt{v_s}}\text{d}s}$

$W_{v,t}^{\ast }=W_{v,t}+{\displaystyle {\int }_0^t{\gamma }_s\text{d}s}$

式中， ${\gamma }_t,t\in \left[0,T\right]$ 是任意 $F_t$ 可测过程。不妨取 ${\theta }_t^{\left(1\right)}=\frac{\mu +r_t-{\delta }_t}{\sqrt{v_s}},{\theta }_t^{\left(2\right)}={\gamma }_t=-\frac{\rho }{\sqrt{1-{\rho }^2}}{\theta }_t^{\left(1\right)}$，根据Girsanov定理，定义Q的等价鞅测度 $Q^{\text{*}}$

$\frac{\text{d}{Q}^{*}}{\text{d}Q}=\exp \left\{-\frac{1}{2}{\displaystyle {\int }_0^T{\left({\theta }_s^{\left(1\right)}\right)}^2+{\left({\theta }_s^{\left(2\right)}\right)}^2\text{d}s}-{\displaystyle {\int }_0^T{\theta }_s^{\left(1\right)}\text{d}{W}_{S,s}}-{\displaystyle {\int }_0^T{\theta }_s^{\left(2\right)}\text{d}{W}_{v,s}}\right\}$

则 $\left(W_{S,t}^{\ast },W_{v,t}^{\ast }\right)$ 在测度 $Q^{\text{*}}$ 下为二维布朗运动。方程(1)可改写为

$\text{d}{S}_t=\sqrt{v_t}{S}_t\text{d}{W}_{S,t}^{\ast }$ (5)

由 $S_{i+1}-S_i={\displaystyle {\int }_{t_i}^{t_{i+1}}\sqrt{v_t}{S}_t\text{d}{W}_{S,t}^{\ast }}$ 利用二维Ito公式得：

$\frac{n}{T}{\left(S_{i+1}-S_i\right)}^2=\frac{n}{T}{\displaystyle {\int }_{t_i}^{t_{i+1}}{v}_t{S}_t^2\text{d}t}+\frac{2n}{T}{\displaystyle {\int }_{t_i}^{t_{i+1}}\left(S_t-S_i\right)S_t\sqrt{v_t}\text{d}{W}_{S,t}^{\ast }}$

记 ${\epsilon }_i=\frac{2n}{T}{\displaystyle {\int }_{t_i}^{t_{i+1}}\left(S_t-S_i\right)S_t\sqrt{v_t}\text{d}{W}_{S,t}^{\ast }}$。由Ito积分的性质知， ${\epsilon }_i,i=1,2,\cdots ,n$ 为鞅差序列，且

$E{\epsilon }_i=\frac{2n}{T}E\left\{{\displaystyle {\int }_{t_i}^{t_{i+1}}\left(S_t-S_i\right)S_t\sqrt{v_t}\text{d}{W}_{S,t}^{\ast }}\right\}=0$

于是有如下近似式：

$\frac{n}{T}{\left(S_{i+1}-S_i\right)}^2\approx v_i{S}_i^2$

故有

$v_i\approx \frac{n{\left(S_{i+1}-S_i\right)}^2}{T{S}_i^2},i=0,1,\cdots ,n-1$

这样我们便得到了随机波动率过程 $v_t$ 的样本。

过程 $v_t$ 的不变分布的均值和方差分别为

$E\left(v_t\right)=\theta$ , $Cov\left(v_t\right)=\frac{{\sigma }_v^2}{2k_v}\theta$

由于 $v_t$ 过程具有均值和方差的各态历经性，因而可分别构造均值 $\theta$，方差 $Cov=\frac{{\sigma }_v^2}{2k_v}\theta$ 矩估计

$\hat{\theta }=\frac{1}{n-n_0}{\displaystyle \underset{t=n_0+1}{\overset{n}{\sum }}{v}_t}$ , $C\hat{o}v=\frac{1}{n-n_0}{\displaystyle \underset{t=n_0+1}{\overset{n}{\sum }}{v}_t^2-{\hat{\theta }}^2}$

式中 $n_0$ 是一个适当的数，由过程 $\left\{v_t,t\ge 0\right\}$ 从0时刻的初值 $v_0$ 达到稳定所要的时间决定。于是

${\sigma }_v^2=\frac{2C\hat{o}v}{\hat{\theta }}{\hat{k}}_v$ (6)

这就得到了当过程的平稳均值与平稳方差确定时，参数 $k_v$ 和 ${\sigma }_v$ 的关系。文献 [17] 给出了随机波动率的条件期望为

$E\left(v_{i+1}|v_i\right)={\text{e}}^{-k_v}{v}_i+\theta \left(1-{\text{e}}^{-k_v}\right)$ , $i=0,1,\cdots ,n-1$

Robigon [18] 给出了时间序列 $v_i,i=1,\cdots ,n$ 的条件均值 $\xi \left(v\right)=E\left(v_{i+1}|v_i=v\right)$ 的核估计并讨论了它们的渐进性质。 $\xi \left(v\right)$ 的核估计为

$\hat{\xi }\left(v\right)=\frac{\frac{1}{n-1}{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}{v}_{i+1}K\left\{h_n^{-1}\left(v-v_i\right)\right\}}}{\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}K\left\{h_n^{-1}\left(v-v_i\right)\right\}}}$

式中 $K(\cdot )$ 为核函数， $h_n$ 为带宽，满足条件：当 $n\to \infty$ 时， $h_n\to \text{0}$，而 $n{h}_n\to \infty$。只要得到 $\xi \left(v_i\right)=E\left(v_{i+1}|v_i\right)$， $i=0,\cdots ,n-1$ 的估计量，则利用非线性最小二乘法就可得到 $k_v$ 的估计值，再利用式(6)求得 ${\sigma }_v$ 的估计值。

随机波动率的条件均值呈标准正态分布，本文核函数取为

$K\left(x\right)=\frac{1}{\sqrt{2\pi }}{\text{e}}^{-\frac{x^2}{2}}$

带宽 $h_n$ 的取值通过试算决定，选取 $h_n$ 使 $\left(v_i,\xi \left(v_i\right)\right)$ 的散点图有较强的回归趋势。见图1，图1(a)~(d)给出了 $h_n$ 分别取0.02，0.05，0.2，0.5时的散点图。从图中可见 $h_n$ 应取0.5。

(a) h_n = 0.02 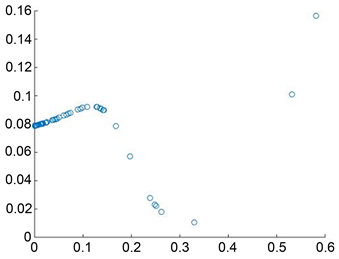(b) h_n = 0.05 (c) h_n = 0.2 (d) h_n = 0.5

Figure 1. $\left(v_i,\xi \left(v_i\right)\right)$ Scatter plot

图1. $\left(v_i,\xi \left(v_i\right)\right)$ 散点图

接下来对式(2)、(3)中的参数进行估计。本文所提模型为状态空间模型，可以用卡尔曼滤波方法对模型中的参数进行估计。下面以2010年1月至2015年12月美国LNG进口价格数据(www.eia.gov)为样本，对模型中的参数进行估计。参数估计值见表1。

Table 1. Parameter estimates

表1. 参数估计值

3. 模型的验证和分析

下面以2016年1月至2018年12月的数据作为样本外预测区间。

由(2)(3)得：

$r_T=m+\left(r_t-m\right){\text{e}}^{-k_r\left(T-t\right)}+{\text{e}}^{-k_{r}T}{\displaystyle {\int }_t^T{\sigma }_r{\text{e}}^{k_{r}u}\text{d}{W}_{r,u}}$ (7)

${\delta }_t=\alpha +\left({\delta }_t-\alpha \right){\text{e}}^{-k_{\delta }\left(T-t\right)}+{\text{e}}^{-k_{\delta }T}{\displaystyle {\int }_t^T{\sigma }_{\delta }{\text{e}}^{k_{\delta }u}\text{d}{W}_{\delta ,u}}$ (8)

将式(7)、(8)以及各参数的值代入(1)中，利用(9)递推公式，即可求得LNG价格的数值，如图2所示。

$S_{t+1}=S_t\left(1+\mu +r_t-{\delta }_t+\sqrt{v_t}{W}_{v,t}\right)$ (9)

其中， $W_{v,t}$ 是正态随机数。

Figure 2. Comparison of natural gas prices

图2. 天然气价格对比图

图2分别给出天然气市场价格、考虑随机波动率得到的价格以及不考虑随机波动率的价格。从图中可以看出，考虑随机波动率模型的拟合效果比不考虑随机波动率的拟合效果更好，更贴近市场价格，尤其是在2016年4月和2017年9月，当天然气价格出现大幅波动，分别出现大幅上升和下降时拟合效果更佳。这是因为考虑随机波动率模型，对价格波动较大的情况更敏感，因此本文所提模型可以更好的对LNG远期定价。

实际值和预测值的差即为拟合误差，分别采用均方根误差(RMSE)和平均绝对误差(M。AE)统计量，评价本文所提出的LNG远期定价模型的拟合和预测能力。

$\text{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}{\left({\hat{S}}_t-S_t\right)}^2}}$

$\text{MAE}=\frac{1}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}\left|{\hat{S}}_t-S_t\right|}$

其中， ${\hat{S}}_t$ 为预测值， $S_t$ 为实际值。通过计算得到： $\text{RMSE}=0.0197$ , $\text{MAE}=0.0134$，模型拟合和预测的均方根误差和平均绝对误差的值较小，均不超过2%，因此说模型的拟合和预测能力较好。

4. 结论

本文在LNG价格的收益率和便利收益服从均值回复的基础上，考虑随机波动率因素，用等价鞅测度和伊藤公式等方法求解模型，并用矩估计法得到模型中的参数，进而得到远期价格的数值解。实证表明，随机波动率的模型拟合效果更好，具有较好的适应性。