1. 引言
在淡水生态系统中,浮游植物一直扮演着重要角色,它处于食物链第一营养级,通常被认为是鱼类和其他水生动物的重要食物来源 [1]。此外,通过光合作用,浮游植物能够吸收大量的二氧化碳并释放氧气。然而,近些年由于浮游植物水华暴发,给环境和人类健康产生了严重的负面影响 [2] [3]。
由于现代经济的快速发展和人口的急剧增加,大量的生活污水和工业污染物排入水体,导致氮、磷等营养物质在湖泊和水库中大量积累,加速了水体富营养化的进程。水体富营养化促进了浮游植物的大量繁殖,进而频繁引发浮游植物水华事件。浮游植物水华能产生一系列的严重后果,例如:导致鱼类的大量死亡 [4];此外,一些藻类还分泌毒素,导致鱼类、鸟类等动物中毒;通过食物链还能间接对人类健康造成影响 [5] [6] [7] [8] 等。因此,研究如何控制浮游植物的增长具有重要意义。
1932年,Bertalanffy首次运用数学模型研究生物系统中存在的问题 [9],数学模型在生物邻域中显示出越来越强大的生命力。近些年,越来越多的科学家试图用数学模型来研究生物种群增长和分布的动态变化过程,例如,时滞动力学模型 [10] [11]、扩散动力学模型 [12] [13] 和脉冲动力学模型 [14] [15] 等。在许多现实问题中,浮游植物种群状态的变化可能既不是连续的,也不是离散的,而是同时存在的,从而导致脉冲控制动力学系统成为当前研究的热点。
脉冲控制动力学系统主要分为三类:脉冲发生在固定时刻,脉冲发生在可变时刻,依赖于状态的脉冲控制。在许多生态系统中,可以利用脉冲微分方程 [16] - [25] 来描述系统中发生的瞬时突变问题。近年来,对带有脉冲控制动力系统的研究取得了显著的成果。其中,许多学者对脉冲发生在固定时刻的动力系统进行了大量研究,如传染病脉冲动力学模型和药代动力学模型等 [26] [27] [28]。然而,针对生态系统中的一些问题,控制措施的实施通常依据种群增长的状态,显然此时状态依赖脉冲似乎比固定周期脉冲要更适合,例如水华控制、害虫暴发控制 [29] [30] [31] [32] 等。
Huppert等人 [33] 提出了一个N-P模型来描述营养驱动的浮游植物水华的动力学:
(1.1)
同时结论表明,在浮游植物暴发之前,需要大量的营养物质。也就是说,只有当营养物质超过一定的限定水平时,才会触发水华。在此模型的基础上,大量研究者通过考虑时滞或扩散等因素进一步研究N-P模型的动力学性质 [34] - [39]。给予状态依赖脉冲微分方程,本文在模型(1.1)的基础上提出了一类具有异步控制的营养–浮游植物动力学模型,如下:
(1.2)
其中
和
分别为营养水平和浮游植物密度,I为流入系统中的营养,a为浮游植物的吸收率,e为营养的损失率,
为转化率,m为浮游植物的死亡率,且
为预警值,
为暴发临界值,当浮游植物达到预警值
时,采取控制措施,使得营养和浮游植物密度为
和
,当浮游植物达到临界值
时,在采取控制措施后,营养和浮游植物密度为
和
,其中
且
。
本文共分为四部分:在第二部分介绍基础知识,包括一些主要定义与引理;第三部分,对系统进行动力学分析;在第四部分,得出结论。
2. 基础知识
定义2.1 [40] [41] 设状态脉冲微分方程
(2.1)
我们把由“状态脉冲微分方程”(2.1)所定义的解映射所构成的“动力学系统”称为半连续动力系统,记为
。我们规定系统的映射初始点P不能在脉冲集上,
,
为连续映射,
,
称为脉冲映射。这里
和
为
平面上的直线或曲线,
称为脉冲集,
称为相集。
定义2.2 [42] 统(2.1)中,在相集N上建立坐标系,假设相集N交x轴于点Q,令点Q的坐标等0。
,令点A的坐标等于点A与点Q的距离,记为a。假设过点A的系统的轨线经过k次脉冲作用后交N于点
,记的坐标为
,则点
称作点A的阶k后继点;函数
称作点A的阶k后继函数,
。
引理 2.1 若
,则从A点出发的轨线是系统的阶1周期解。
引理 2.2 根据引理1.1可知
是半连续动力系统,若存在
,满足
,则在
之间存在A,使得
,根据引理2.1,系统存在阶1周期解。
3. 动力学分析
显然,
和
是模型(1.2)的平衡点,且可以得到三条等倾线:
,
和
。当
时,
,当
时,
,记脉冲集
为P,
为M,
为相集N。
模型(1.2)水平等倾线与相集N交于点
,与脉冲集P交于点
。当
时,在相集N上存在点
,使得从点
出发的轨线首次交脉冲集P于点
。由于脉冲作用到达点
,根据微分方程轨线的不相交性,以及脉冲函数
可知,对于位于
左侧的点(如图1所示),任取点A位于相集N上的子集合
,显然在
上有
。从点A出发的轨线
交脉冲集P于点
,由于脉冲作用到达
。点
出发的轨线
交脉冲集M于点
,由于脉冲作用交N于点
。此时,存在映射
,即对
,
,使得
,其中
,
,
,
。
但是在脉冲集P上,当
时,P上存在子集合
,存在一个映射
(如图2所示),
,
,使得
,其中
,
。
引理3.1 映射
为连续的一一映射。
首先本文考虑
,对
上任意点A,从点A出发的轨线一定与脉冲集M相交,然后通过脉冲作用到达相集N上。若在
存在两点
,使得
,由
可知,
,这个时候,从两个不同点出发的轨线交于同一点,与微分方程轨线的不相交性互相矛盾,所以映射f为一一映射。
接下来考虑连续性:
因为
在
处连续,所以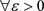 ,
,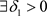 ,当
,当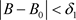 时,有
时,有 ,由于微分方程的解对初始条件是连续依赖的,所以
,由于微分方程的解对初始条件是连续依赖的,所以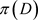 在
在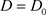 处连续。因此,对
处连续。因此,对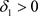 ,
,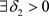 ,当
,当 时,有
时,有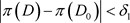 。同理,根据
。同理,根据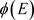 在
在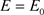 处连续性,对
处连续性,对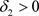 ,
,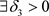 ,当
,当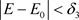 时,有
时,有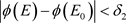 。最后,根据微分方程的解对初始条件是连续依赖的,可知,
。最后,根据微分方程的解对初始条件是连续依赖的,可知,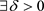 ,当
,当 时,有
时,有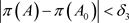 ,其中
,其中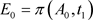 ,
,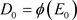 ,
,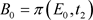 ,
,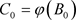 。所以,
。所以,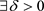 ,当
,当 时,有
时,有 ,则
,则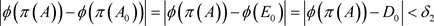 。近一步,我们有
。近一步,我们有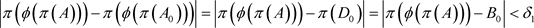 。因此,
。因此,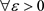 ,
, ,并
,并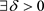 ,当
,当 时,有
时,有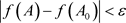 ,所以映射f为连续的。
,所以映射f为连续的。
综上所述,映射 为连续的一一映射。
为连续的一一映射。
证毕。
引理3.2 映射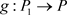 为连续的一一映射。
为连续的一一映射。
证明:由于此证明方法与上述证明相似,故省略。
由上述映射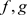 为连续的一一映射,对
为连续的一一映射,对 或
或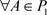 ,相集N上的阶一后继函数
,相集N上的阶一后继函数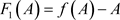 与集合P上的阶一后继函数
与集合P上的阶一后继函数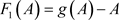 为连续的,可得以下引理。
为连续的,可得以下引理。
引理3.3 在系统(1.2)中,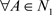 或
或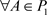 ,其阶一后继函数
,其阶一后继函数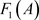 是连续的。
是连续的。
接下来我们探讨系统(1.2)中的周期解,首先,由于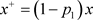 ,对任意
,对任意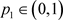 ,当
,当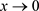 时,有
时,有 。因此,当
。因此,当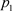 为固定值时,在相集N上存在点
为固定值时,在相集N上存在点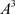 ,使得从点
,使得从点 出发的轨线交脉冲集P于点
出发的轨线交脉冲集P于点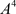 ,由于脉冲作用到达点
,由于脉冲作用到达点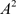 ,即,
,即,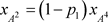 。故考虑以下两种情况:(1)
。故考虑以下两种情况:(1) 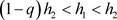 (2)
(2)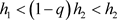 。
。
情况(1)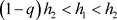 :
:
定理31系统(12)存在阶一周期解。
证明:存在点 ,使得从点B出发的轨线与脉冲集P交于点
,使得从点B出发的轨线与脉冲集P交于点 ,而
,而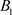 在
在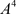 的左侧,即
的左侧,即 ,由于脉冲作用,点
,由于脉冲作用,点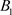 沿着脉冲集P向左平移到
沿着脉冲集P向左平移到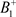 ,此时
,此时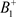 与B的位置关系如下:(a):
与B的位置关系如下:(a):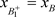 ;(b):
;(b):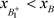 ;(c):
;(c):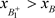
(a):当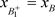 时(图3),即点
时(图3),即点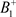 与B重合,则闭轨
与B重合,则闭轨 为阶一周期解。
为阶一周期解。
(b):当 时(图4),即B的阶一后继函数为
时(图4),即B的阶一后继函数为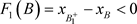 。以
。以 为初始点出发的轨线与P交于点
为初始点出发的轨线与P交于点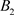 ,由于轨线互不相交, 所以
,由于轨线互不相交, 所以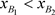 。经过脉冲作用后到达点
。经过脉冲作用后到达点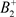 ,此时
,此时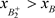 ,因此
,因此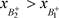 。
。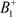 的阶一后继函数为
的阶一后继函数为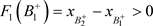 ,故
,故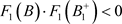 ,根据引理13,系统(12)存在阶一周期解。
,根据引理13,系统(12)存在阶一周期解。
(c):当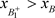 时(图5),即B的阶一后继函数为
时(图5),即B的阶一后继函数为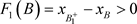 。以
。以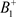 为初始点出发的轨线与P交于点
为初始点出发的轨线与P交于点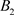 ,由于轨线的不相交性,
,由于轨线的不相交性,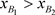 ,由于脉冲作用,到达点
,由于脉冲作用,到达点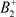 ,此时
,此时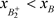 ,所以
,所以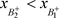 ,
,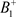 的阶一后继函数为
的阶一后继函数为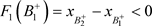 ,所以
,所以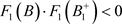 ,根据引理13,系统(12)存在阶一周期解。
,根据引理13,系统(12)存在阶一周期解。
证毕。
定理3.2当存在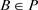 ,使得
,使得 ,此时系统(1.2)存在唯一的正的阶一周期解。
,此时系统(1.2)存在唯一的正的阶一周期解。
证明:当存在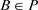 ,使得
,使得 时,假设存在两个正的阶一周期间,为闭轨
时,假设存在两个正的阶一周期间,为闭轨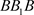 和闭轨
和闭轨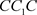 ,如下图6所示。由于
,如下图6所示。由于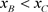 且
且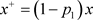 ,故
,故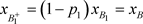 ,
,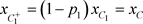 。因为
。因为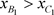 ,
,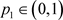 ,所以
,所以 ,因此
,因此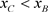 。显然矛盾,系统(1.2)存在唯一的正的阶一周期解。
。显然矛盾,系统(1.2)存在唯一的正的阶一周期解。
证毕。
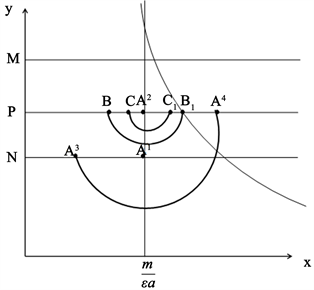
Figure 6. The order-1 periodic solution of system (1.2)
图6. 系统(1.2)的阶一周期解
定理3.3 当存在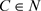 ,使得
,使得 ,则系统(1.2)存在阶一周期解。
,则系统(1.2)存在阶一周期解。
证明:在相集N上取点C,使得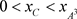 ,从点C出发的轨线与脉冲集P交于点
,从点C出发的轨线与脉冲集P交于点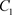 ,由于脉冲作用到达
,由于脉冲作用到达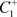 ,从点
,从点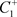 出发的轨线与脉冲集M交于点
出发的轨线与脉冲集M交于点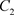 ,经过脉冲作用跳到N上于点
,经过脉冲作用跳到N上于点 ,此时
,此时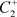 的位置有以下三种情况:(a):
的位置有以下三种情况:(a):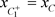 ;(b):
;(b):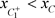 ;(c):
;(c):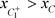 。
。
(a):当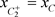 时(图7),即点
时(图7),即点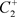 与C重合,系统(1.2)存在阶一周期解。
与C重合,系统(1.2)存在阶一周期解。
(b):当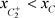 时(图8),即,
时(图8),即,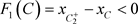 。假设相集N与y轴交于点D,以D为初始点出发的轨线与P交于点
。假设相集N与y轴交于点D,以D为初始点出发的轨线与P交于点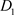 ,经过脉冲作用后到达点
,经过脉冲作用后到达点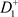 ,从
,从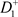 出发的轨线交脉冲集M于点
出发的轨线交脉冲集M于点 ,由于脉冲作用交N于
,由于脉冲作用交N于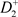 。由于
。由于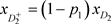 ,
,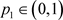 ,且
,且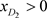 ,所以
,所以 ,因此
,因此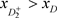 。即,D的阶一后继函数为
。即,D的阶一后继函数为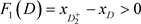 ,则
,则 ,根据引理1.3,系统(1.2)存在阶一周期解。
,根据引理1.3,系统(1.2)存在阶一周期解。
(c):当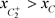 时(图9),即
时(图9),即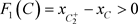 。以
。以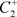 为初始点出发的轨线与P交于点
为初始点出发的轨线与P交于点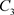 ,由于脉冲作用,到达点
,由于脉冲作用,到达点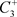 。从
。从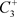 出发的轨线交脉冲集M于点
出发的轨线交脉冲集M于点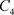 ,经过脉冲作用交N于
,经过脉冲作用交N于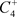 ,根据轨线的不相交性,故
,根据轨线的不相交性,故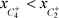 。即
。即 ,所以
,所以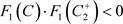 ,根据引理1.3,系统(1.2)存在阶一周期解。
,根据引理1.3,系统(1.2)存在阶一周期解。
证毕。
情况(2) 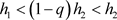
定理3.4 当存在 ,使得
,使得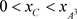 时,系统(1.2)存在阶一周期解。
时,系统(1.2)存在阶一周期解。
证明:在相集N上取点C,使得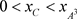 ,从点C出发的轨线与脉冲集P交于点
,从点C出发的轨线与脉冲集P交于点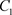 ,由于脉冲作用到达
,由于脉冲作用到达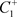 ,从点
,从点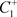 出发的轨线与脉冲集M交于点
出发的轨线与脉冲集M交于点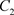 ,经过脉冲作用跳到N上于点
,经过脉冲作用跳到N上于点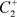 ,此时
,此时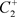 的位置有以下三种情况:(a):
的位置有以下三种情况:(a):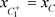 ;(b):
;(b):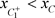 ;(c):
;(c):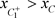
具体证明方法与定理3.3类似,故省略。
定理3.5 当存在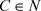 ,使得
,使得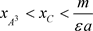 时,系统存在至少两个阶一周期解
时,系统存在至少两个阶一周期解
证明:首先在脉冲集P上的阶一周期解,其证明过程与定理3.1类似,此处省略。
接下来证明另外一个周期解,在点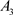 与点
与点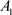 之间任取点C,使得从C点出发的轨线与于点P不相交,则交M于点
之间任取点C,使得从C点出发的轨线与于点P不相交,则交M于点 。由于脉冲作用交N于点
。由于脉冲作用交N于点 ,此时
,此时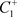 是C的后继点。由定义2.1可知,C的后继函数为
是C的后继点。由定义2.1可知,C的后继函数为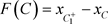 。依据后继点的位置,可分为以下三种情况:
。依据后继点的位置,可分为以下三种情况:
(a):若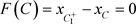 (图10),即点
(图10),即点 与点C重合,则闭环
与点C重合,则闭环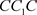 为其阶一周期解。
为其阶一周期解。
(b):若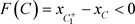 (图11),意味着
(图11),意味着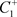 跳到了C的左侧。即
跳到了C的左侧。即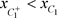 。从
。从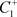 出发的轨线交M于点
出发的轨线交M于点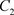 ,经过脉冲作用交N于点
,经过脉冲作用交N于点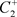 。由于脉冲线互不相交,所以
。由于脉冲线互不相交,所以 ,故
,故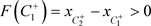 。根据引理1.3,
。根据引理1.3,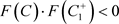 ,所以系统(1.2)存在阶1周期解。
,所以系统(1.2)存在阶1周期解。
(c):若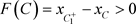 (图12),意味着
(图12),意味着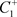 跳到了C的右侧,即
跳到了C的右侧,即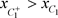 。从
。从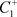 出发的轨线交M于点
出发的轨线交M于点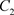 ,经过脉冲作用交N于点
,经过脉冲作用交N于点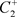 。由于脉冲线互不相交,所以
。由于脉冲线互不相交,所以 ,故
,故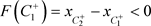 。根据引理1.3,
。根据引理1.3,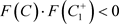 ,所以系统(1.2)存在阶1周期解。
,所以系统(1.2)存在阶1周期解。
证毕。
4. 结论
本文提出了一类具有异步控制的营养盐–浮游植物模型来研究浮游植物种群增长控制动力学性质。充沛的营养物质是浮游植物水华暴发的主因之一。因此,首先设立预警值,当浮游植物种群密度达到预警值时,通过控制营养物质的浓度来限制浮游植物的增长;其次,设立暴发临界值,当浮游植物种群密度达到临界值时,同时控制其营养盐浓度,浮游植物种群密度。本文通过对模型分析,发现对浮游植物种群增长的异步控制下能存在周期解。特别地,我们得到了阶一周期解存在的充分条件。
致谢
首先,我向我的导师赵敏教授表达我最真挚的感谢!老师严谨求实的治学态度,刻苦钻研的精神都对我产生了深刻的影响。感谢老师对我的论文悉心的指导,感谢老师在生活及学习上对我倾注的鼓励和关怀。
其次,感谢我们实验室的于恒国师兄和戴传军师兄,感谢你们不厌其烦地指点我,使我在学习过程中更迅速的汲取更全面的专业知识,感谢我的师兄,师姐,师妹,师弟以及同门们,和他们在学习,生活上的交流,使我不断提高,不断对生活充满信心。
感谢温州大学数学与信息科学院的各位老师和领导,为我们创造了良好的学习环境,感谢他们给予的帮助。
最后,衷心的感谢各位专家学者百忙之中抽时间对本文进行审阅。