一类非线性伪抛物型方程解的性质

Properties of Solutions for a Class of Nonlinear Pseudoparabolic Equations

摘要: 本文研究了一类分数阶非线性伪抛物方程的弱解问题。首先通过能量方法讨论得到方程解的先验估计，然后利用Galerkin方法构造近似解序列来证明方程弱解的存在唯一性。

Abstract: This paper studies the weak solutions of a class of fractional nonlinear pseudo-parabolic equations. First, a priori estimates of the solution of the equation are obtained through the energy method discussion, and then the Galerkin method is used to construct an approximate solution sequence to prove the existence and uniqueness of the weak solution of the equation.

1. 引言

我们考虑分数阶非线性伪抛物方程的以下初始边值问题

$u_t+{\left(-\Delta \right)}^{\alpha }{u}_t+{\left(-\Delta \right)}^{\alpha }u-\mu \left(\nabla u\right)\Delta u+\left(1+\sigma \left(\nabla u\right)\right)u=f\left(x,t\right),$ (1)

${u\left(x,t\right)|}_{x\in \partial \Omega }=0,$ (2)

$u\left(x,0\right)={\tilde{u}}_0\left(x\right),$ (3)

其中 $t>0,x\in \Omega ,\Omega \subset R$ 是有界光滑域，T和 $\alpha$ 是正常数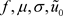，是满足后面指定条件的给定函数。

伪抛物线方程

$u_t-u_{xxt}=F\left(x,t,u_x,u_{xx}\right)\text{,}$ (4)

由Coleman等人于20世纪60年代发现，用来模拟不稳定的简单剪切流的特殊运动状态 [1]。伪抛物线方程用于各种领域，例如均匀流体通过裂隙岩石的渗漏 [2] (三阶项的系数表示岩石的裂隙程度，其减小程度对应于增加裂纹的程度)，非线性色散长波的单向传播 [3] [4] (其中u是振幅或旋度)，种族迁移的描述 [5] (其中u是人口密度)。由于伪抛物线方程的广泛应用，它们引起了数学家的极大关注，例如讨论了解的存在性、渐近行为、正则性和衰减性 [6] [7] [8] [9]。

描述小振幅长波在非线性色散介质中的传播过程时，经典的伪抛物线方程通常必须考虑耗散机制，以便准确反映实际情况。但是，引起波衰减的机制非常复杂，人们对其了解不多。在这种情况下，人们可能被迫依赖耗散的临时模型 [10]。在对平面波的单向传播进行建模时，需要在模型中增加非线性和色散的耗散，如下式

$u_t+u_x+u{u}_x-v{u}_{xx}-u_{xxt}=0,$ (5)

其中 $v>0$ 是固定常数。方程(5)有时被称为Benjamin-Bona-Mahony-Burgers (BBMB)方程，它是Benjamin-Bona-Mahony (BBM)方程 [3] 和Burgers类型耗散项 [8] 的结合。最近，许多科学家开始注意到出现在工程学和物理学中的三级流体流动数学模型框架中的BBMB方程 [11] [12] [13]。T.Aziz等人研究了以下的BBMB运动方程

$\rho u_t=\mu u_{yy}+{\alpha }_1{u}_{yyt}+6{\beta }_3{\left(u_{yy}\right)}^2{u}_{yy}-\frac{\phi }{k}\left(\mu u+{\alpha }_1{u}_t+2{\beta }_3{\left(u_y\right)}^{2}u\right),$ (6)

其中 $y>0,t>0$，u表示速度分量， $\mu$ 表示粘度系数， ${\alpha }_1$ 和 ${\beta }_3$ 是材料常数 [11]。方程(6)适用于带有多孔介质的刚性板上非定常流动三级流体的数学模型。后来，在 [14] (可以看作 [11] 的延续)中，作者在如下改进的非定常流动三级流体方程中证明了解的存在性，唯一性和指数衰减

$u_t+\alpha \left(-\Delta \right)u_t+\left(-\Delta \right)u-\mu \left(\nabla u\right)\Delta u+\left(\gamma +\beta \sigma \left(\nabla u\right)\right)u=f\left(x,t\right),$ (7)

其中 $\alpha =\beta =\gamma =1,\mu \in C\left(R;R\right),\sigma \in C^1\left(R;R\right)$ 和 $y\left({\displaystyle {\int }_0^{y}z{\sigma }^{\prime }\left(z\right)\text{d}z}\right)\le y^2\sigma \left(y\right)\left(y\in R\right)$。

分数耗散算子 ${\left(-\Delta \right)}^{\alpha }$ 可以看作是Levy稳定扩散过程的无穷小生成器。与微积分方程相比，它可以更准确地描述某些物理现象 [15] [16] [17]。因此，越来越多的科学家致力于分数阶微分方程的研究 [16] [17] [18]。

基于以上工作，我们研究了分数阶方程(1)-(3)的弱解的存在性和唯一性。

2. 预备知识和引理

现对文中将用到的定义、引理和记号做一些说明。记函数空间 $L^2\left(\Omega \right)$ 的范数通常表示为 $\Vert \cdot \Vert$，其标量积由 $\langle \cdot \text{,}\cdot \rangle$ 表示， $L^p\left(\Omega \right)$ 的范数记为 ${\Vert \cdot \Vert }_{L^p\left(\Omega \right)}$，C表示一个正常数，该常数可能在各行之间变化。

定义1：范数 $L^p\left(0,T;X\right)$ 表示实函数 $f:\left[0,T\right]\to X$ 的Banach空间，使得

${\Vert f\Vert }_{L^p\left(0,T\text{;}X\right)}={\left({\displaystyle {\int }_0^T{\Vert f\Vert }_X^p\text{d}t}\right)}^{\frac{1}{p}}<\infty ,1\le p<\infty ,$

且

${\Vert f\Vert }_{L^{\infty }\left(0,T;X\right)}=\underset{0\le t\le T}{\text{esssup}}{\Vert f\Vert }_X\text{,}p=\infty .$

引理1：令 $\sigma$ 和 $\mu$ 均是 $R\to R$ 上映射并且属于C，那么

${\Vert \mu \left(\nabla v\right)\Vert }_{L^{\infty }\left(\Omega \right)}<C,$ (8)

${\Vert \sigma \left(\nabla v\right)\Vert }_{L^{\infty }\left(\Omega \right)}<C,$ (9)

其中 $v\in H^{\alpha +1}\left(\Omega \right)$ 且常数C依赖于v。

证明：利用Gagliardo-Nirenberg不等式，有

${\Vert \nabla v\Vert }_{L^{\infty }\left(\Omega \right)}\le c_2{\Vert v\Vert }_{H^{\alpha }\left(\Omega \right)}^{\eta }{\Vert v\Vert }^{1-\eta }<C.$ (10)

其中 $\eta =\frac{n}{2\alpha }+\frac{1}{\alpha }$。应用这个不等式，易知

${\Vert \mu \left(\nabla v\right)\Vert }_{L^{\infty }\left(\Omega \right)}<C,$ (11)

${\Vert \sigma \left(\nabla v\right)\Vert }_{L^{\infty }\left(\Omega \right)}<C.$ (12)

引理2：对于 $\alpha \ge \frac{1}{2}$，令初值满足 ${\tilde{u}}_0\left(x\right)\in H^{\alpha }\left(\Omega \right)$，且

$\mu \in C\left(R;R\right),\mu \left(0\right)=0,\mu \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (13)

$\sigma \in C^1\left(R;R\right),\sigma \left(0\right)=0,\sigma \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (14)

$f\in L^2(\Omega ),$ (15)

那么问题(1)-(3)有一个弱解u，满足

${\Vert u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\le C.$ (16)

证明：将(1)乘以 $u\left(t\right)$，并关于空间变量x在 $\Omega$ 上进行积分，我们很容易就得出了等式

$\frac{1}{2}\frac{\text{d}}{\text{d}t}{\Vert u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2+{\Vert u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2+I_1+I_2=\langle f\left(t\right),u\left(t\right)\rangle ,$ (17)

其中 $I_1=-\langle \mu \left(\nabla u\left(t\right)\right)\Delta u\left(t\right),u\left(t\right)\rangle$， $I_2=\langle \sigma \left(\nabla u\left(t\right)\right)u\left(t\right),u\left(t\right)\rangle$。

估计 $I_1$。易知

$\begin{array}{c}{I}_1=-\langle \mu \left(\nabla u\left(t\right)\right)\Delta u\left(t\right),u\left(t\right)\rangle \\ =-{\displaystyle {\int }_{\Omega }\nabla }\left({\displaystyle {\int }_0^{\nabla u\left(t\right)}\mu }\left(z\right)dz\right)u\left(t\right)\text{d}x\\ ={\displaystyle {\int }_{\Omega }\left({\displaystyle {\int }_0^{\nabla u\left(t\right)}\mu }\left(z\right)dz\right)\nabla u\left(t\right)\text{d}x}\\ \ge 0.\end{array}$ (18)

估计 $I_2$。考虑(14)，易得

$I_2=\langle \sigma \left(\nabla u\left(t\right)\right)u\left(t\right),u\left(t\right)\rangle \ge 0.$ (19)

回顾(17)，从(18)-(19)可得

$\frac{\text{d}}{\text{d}t}{\Vert u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2+{\Vert u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\le C,$ (20)

其中C依赖f。那么运用~Gronwall~引理，可推断出

${\Vert u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\le C.$ (21)

引理2：假设 $\alpha \ge \frac{1}{2}$， ${\tilde{u}}_0\left(x\right)\in H^{\alpha +1}\left(\Omega \right)$，且

$\mu \in C\left(R;R\right),\mu \left(0\right)=0,\mu \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (22)

$\sigma \in C^1\left(R;R\right),\sigma \left(0\right)=0,\sigma \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (23)

$f\in L^2\left(0,\infty ;H^1\left(\Omega \right)\right).$ (24)

那么问题(1)-(3)有一个弱解u满足

${\Vert \nabla u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\le C.$ (25)

证明：将(1)乘以 $\left(-\Delta \right)u$，关于空间变量x在 $\Omega$ 上进行积分，我们有

$\begin{array}{l}{\Vert \nabla u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2+\langle \mu \left(\nabla u\left(t\right)\right)\Delta u\left(t\right),\Delta u\left(t\right)\rangle +\frac{1}{2}\frac{\text{d}}{\text{d}t}{\Vert \nabla u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\\ +\langle \sigma \left(\nabla u\left(t\right)\right)u\left(t\right),\left(-\Delta \right)u\left(t\right)\rangle =\langle f\left(t\right),\left(-\Delta \right)u\left(t\right)\rangle .\end{array}$ (26)

类似(18)，我们推断

$\langle \sigma \left(\nabla u\left(t\right)\right)u\left(t\right),\left(-\Delta \right)u\left(t\right)\rangle \ge 0.$ (27)

考虑(22)，我们可以获得

$2\langle \mu \left(\nabla u\left(t\right)\right)\Delta u\left(t\right),\Delta u\left(t\right)\rangle \ge 0.$ (28)

另一方面，有

$\langle f\left(t\right),\left(-\Delta \right)u\left(t\right)\rangle \le \Vert \nabla f\left(t\right)\Vert \Vert \nabla u\left(t\right)\Vert \le \frac{1}{2\epsilon }{\Vert \nabla f\left(t\right)\Vert }^2+\frac{\epsilon }{2}{\Vert \nabla u\left(t\right)\Vert }^2,$ (29)

其中 $\epsilon$ 是一个正常数并且充分小。根据(26)-(29)有

$\frac{\text{d}}{\text{d}t}{\Vert \nabla u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2+{\Vert \nabla u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\le C,$ (30)

其中C依赖f。利用Gronwall引理，我们可以推断出

${\Vert \nabla u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\le C.$ (31)

引理3：令 $\alpha \ge \frac{1}{2}$， ${\tilde{u}}_0\left(x\right)\in H^{\alpha +1}\left(\Omega \right)$，u是(1)-(3)有一个弱解，且

$\mu \in C\left(R;R\right),\mu \left(0\right)=0,\mu \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (32)

$\sigma \in C^1\left(R;R\right),\sigma \left(0\right)=0,\sigma \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (33)

$f\in L^2\left(0,\infty ;H^1\left(\Omega \right)\right).$ (34)

满足

$\begin{array}{l}{\displaystyle {\int }_0^t{\Vert u_t\left(s\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\text{d}s}<C.\hfill \end{array}$ (35)

证明：将(1)乘以 $u_t$ 并关于时间变量t和空间变量x在 $\left(0,t\right)\times \Omega$ 上进行积分，整理可得

$\begin{array}{l}{\Vert u\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2+2{\displaystyle {\int }_0^t\langle \sigma \left(\nabla u\left(s\right)\right)u\left(s\right),u_t\left(s\right)\rangle \text{d}s}\\ +2{\displaystyle {\int }_0^t{\Vert u_t\left(s\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2}\text{d}s-2{\displaystyle {\int }_0^t\langle \mu \left(\nabla u\left(s\right)\right)\Delta u\left(s\right),u_t\left(s\right)\rangle \text{d}s}\\ ={\Vert u_0\Vert }_{H^{\alpha }\left(\Omega \right)}^2+2{\displaystyle {\int }_0^t\langle f\left(s\right),u_t\left(s\right)\rangle ds}.\end{array}$ (36)

从(32)，我们可以得到

$-2{\displaystyle {\int }_0^t\langle \mu \left(\nabla u\left(s\right)\right)\Delta u\left(s\right),u_t\left(s\right)\rangle \text{d}s}=2{\displaystyle {\int }_{\Omega }{\displaystyle {\int }_0^{\nabla u\left(t\right)}{\displaystyle {\int }_0^y\mu \left(z\right)\text{d}z\text{d}y\text{d}x}}}\ge 0.$ (37)

考虑(25)和引理1，可以获得

$\begin{array}{l}2\left|{\displaystyle {\int }_0^t\langle \sigma \left(\nabla u\left(s\right)\right)u\left(s\right),u_t\left(s\right)\rangle \text{d}s}\right|\\ \le 2{\Vert \sigma \left(\nabla u\left(s\right)\right)\Vert }_{L^{\infty }\left(\Omega \right)}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\Omega }^{}\left|u\left(s\right)u_t\left(s\right)\right|\text{d}x\text{d}s}}\\ \le C+\delta {\displaystyle {\int }_0^t{\Vert u_t\left(s\right)\Vert }^2}\text{d}s\text{,}\end{array}$ (38)

其中 $\delta$ 是一个正常数。

因此，选择 $\delta$ 充分小，根据(36)-(38)有

$\begin{array}{l}{\displaystyle {\int }_0^t{\Vert u_t\left(s\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2\text{d}s}<C,\hfill \end{array}$ (39)

其中C依赖f。

3. 主要结果及其证明

借助上述引理，我们可以证明下面的定理。

定理1：对于 $\alpha \ge \frac{1}{2}$ 令初值满足 ${\tilde{u}}_0\left(x\right)\in H^{\alpha +1}\left(\Omega \right)$，且

$\mu \in C\left(R;R\right),\mu \left(0\right)=0,\mu \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (40)

$\sigma \in C^1\left(R;R\right),\sigma \left(0\right)=0,\sigma \left(z\right)>0\left(\forall z\in R,z\ne 0\right),$ (41)

$f\in L^2\left(0,\infty ;H^1\left(\Omega \right)\right).$ (42)

那么问题(1)-(3)有一个弱解u，满足

$u\in L^{\infty }\left(0,\infty ;H^{\alpha +1}\left(\Omega \right)\right),u_t\in L^2\left(0,T;H^{\alpha }\left(\Omega \right)\right).$ (43)

证明：第一步：Galerkin逼近

在 $H^{\alpha }$ 上取特殊的正交基 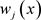$\left\{w_j\right\}$ ：由拉普拉斯特征函数形成：

$\Delta w_j={\lambda }_j{w}_j,w_j\in C^{\infty }\left(\Omega \right),0<{\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_j\to \infty .$ (44)

定义

$u_m\left(t\right)={\displaystyle \underset{j=1}{\overset{m}{\sum }}{c}_{mj}}\left(t\right)w_j,$ (45)

其中 $c_{mj}\left(t\right)\left(j=1,\cdots ,m\right)$ 满足下面逼近方程

$\begin{array}{l}\langle {\left(-\Delta \right)}^{\alpha }{u}_{mt}\left(t\right),w_j\rangle +\langle \left(1+\sigma \left(\nabla u_m\left(t\right)\right)\right)u_m\left(t\right),w_j\rangle +\langle {\left(-\Delta \right)}^{\alpha }{u}_m\left(t\right),w_j\rangle \\ +\langle u_{mt}\left(t\right),w_j\rangle -\langle \mu \left(\nabla u_m\left(t\right)\right)\Delta u_m\left(t\right),w_j\rangle =\langle f\left(t\right),w_j\rangle ,1\le j\le m,\end{array}$ (46)

初始条件

$u_m\left(0\right)=u_{0m}\in span\left\{w_j,1\le j\le m\right\},$

$u_{0m}\to {\tilde{u}}_0\left(m\to \infty \right)$ 在 $H^{\alpha +1}\left(\Omega \right)$ 中强收敛。(47)

显然，此时的方程(46)-(47)是一组常微分方程。应用标准常微分方程的理论，易知当 $0\le t\le t_m=T$ 时，方程(46)-(47)具有唯一解。

第二步：取极限

根据以上估算，存在 $\left\{u_m\left(t\right)\right\}$ 的子序列，仍用 $\left\{u_m\left(t\right)\right\}$ 表示，满足

$u_m\to u$ 在 $L^{\infty }\left(0,\infty ;H^{\alpha +1}\left(\Omega \right)\right)$ 中弱 $\ast$ 收敛， (48)

$u_{mt}\to u_t$ 在 $L^2\left(0,T;H^{\alpha }\left(\Omega \right)\right)$ 中弱 $\ast$ 收敛。 (49)

应用Riesz定理，有

$u_m\to u$ 在 $L^2\left(0,\infty ;H^{\alpha }\left(\Omega \right)\right)$ 中强收敛且几乎处处收敛于 $Q_T$，(50)

$\nabla u_m\to \nabla u$ 在 $L^2\left(Q_T\right)$ 中强收敛且几乎处处收敛于 $Q_T$，(51)

$\Delta u_m\to \Delta u$ 在 $L^2\left(Q_T\right)$ 中强收敛且几乎处处收敛于 $Q_T$。 (52)

考虑引理1、引理2和引理3，我们可以得到

$\begin{array}{l}{\Vert {\displaystyle {\int }_0^{\nabla u_m}\mu \left(z\right)\text{d}z}\Vert }_{L^{\infty }\left(\Omega \right)}<C,\\ {\Vert \sigma \left(\nabla u_m\right)u_m\Vert }_{L^{\infty }\left(\Omega \right)}<C.\end{array}$ (53)

应用控制收敛定理，我们发现

${\displaystyle {\int }_0^{\nabla u_m}\mu }\left(z\right)\text{d}z\to {\displaystyle {\int }_0^{\nabla u}\mu }\left(z\right)\text{d}z$ 在 $L^2\left(Q_T\right)$ 中强收敛， (54)

$\sigma \left(\nabla u_m\right)u_m\to \sigma \left(\nabla u\right)u$ 在 $L^2\left(Q_T\right)$ 中强收敛。 (55)

通过(47)-(52)和(54)-(55)，在(46)中取极限，我们获得

$\begin{array}{l}\langle u_t\left(t\right),w\rangle +\langle {\left(-\Delta \right)}^{\frac{\alpha }{2}}u\left(t\right),{\left(-\Delta \right)}^{\frac{\alpha }{2}}w\rangle +\langle {\displaystyle {\int }_0^{\nabla u\left(t\right)}\mu }\left(z\right)\text{d}z,\nabla w\rangle \\ +\langle {\left(-\Delta \right)}^{\alpha }{u}_t\left(t\right),{\left(-\Delta \right)}^{\frac{\alpha }{2}}w\rangle +\langle \left(1+\sigma \left(\nabla u\left(t\right)\right)\right)u\left(t\right),w\rangle \\ =\langle f\left(t\right),w\rangle ,\forall w\in H^{\alpha }\left(\Omega \right),\\ u\left(0\right)={\tilde{u}}_0.\end{array}$ (56)

另外

$u\in L^{\infty }\left(0,\infty ;H^{\alpha +1}\left(\Omega \right)\right),u_t\in L^2\left(0,T;H^{\alpha }\left(\Omega \right)\right).$ (57)

第三步：解的唯一性

令u和v是(1)-(3)的弱解。定义 $w=u-v$，我们有

$\begin{array}{l}{w}_t+{\left(-\Delta \right)}^{\alpha }{w}_t+{\left(-\Delta \right)}^{\alpha }w-\left(\mu \left(\nabla u\right)\Delta u-\mu \left(\nabla v\right)\Delta v\right)\\ +w+\left(\sigma \left(\nabla u\right)u-\sigma \left(\nabla v\right)v\right)=0,\\ w\left(0\right)=0.\end{array}$ (58)

将(58)与w相乘，然后关于时间变量t和空间变量x从 $\left(0,t\right)\times \Omega$ 进行积分，我们得到

$\begin{array}{l}{\Vert w\left(t\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2-2{\displaystyle {\int }_0^t\langle \mu \left(\nabla u\left(s\right)\right)\Delta u\left(s\right)-\mu \left(\nabla v\left(s\right)\right)\Delta v\left(s\right),w\left(s\right)\rangle \text{d}s}\\ +2{\displaystyle {\int }_0^t{\Vert w\left(s\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2}\text{d}s+2{\displaystyle {\int }_0^t\langle \sigma \left(\nabla u\left(s\right)\right)u\left(s\right)-\sigma \left(\nabla v\left(s\right)\right)v\left(s\right),w\left(s\right)\rangle \text{d}s}=0.\end{array}$ (59)

利用函数的单调性，我们推断

$\begin{array}{l}-2{\displaystyle {\int }_0^t\langle \mu \left(\nabla u\left(s\right)\right)\Delta u\left(s\right),w\left(s\right)\rangle }-\langle \mu \left(\nabla v\left(s\right)\right)\Delta v\left(s\right),w\left(s\right)\rangle \text{d}s\\ =2{\displaystyle {\int }_0^t\langle {\displaystyle {\int }_0^{\nabla u\left(s\right)}\mu }\left(z\right)\text{d}z-{\displaystyle {\int }_0^{\nabla v\left(s\right)}\mu }\left(z\right)\text{d}z,\nabla w\left(s\right)\rangle \text{d}s}\ge 0.\end{array}$ (60)

另一方面，我们发现

$\begin{array}{l}-2{\displaystyle {\int }_0^t\langle \sigma \left(\nabla u\left(s\right)\right)u\left(s\right)-\sigma \left(\nabla v\left(s\right)\right)v\left(s\right),w\left(s\right)\rangle \text{d}s}\\ =-2{\displaystyle {\int }_0^t[\langle \sigma \left(\nabla u\left(s\right)\right)v\left(s\right),w\left(s\right)\rangle +\langle \sigma \left(\nabla u\left(s\right)\right)w\left(s\right),w\left(s\right)\rangle }\\ -\langle \sigma \left(\nabla v\left(s\right)\right)v\left(s\right),w\left(s\right)\rangle ]\text{d}s.\end{array}$ (61)

利用估计，我们有

$\left|\sigma \left(\nabla v\left(s\right)\right)-\sigma \left(\nabla u\left(s\right)\right)\right|<L_1\left|\nabla v\left(s\right)-\nabla u\left(s\right)\right|,$ (62)

那么，由(62)，可知

$\begin{array}{l}-2{\displaystyle {\int }_0^t\langle \sigma \left(\nabla u\left(s\right)\right)v\left(s\right),w\left(s\right)\rangle }-\langle \sigma \left(\nabla v\left(s\right)\right)v\left(s\right),w\left(s\right)\rangle \text{d}s\\ =2{\displaystyle {\int }_0^t\langle \left(\sigma \left(\nabla v\left(s\right)\right)-\sigma \left(\nabla u\left(s\right)\right)\right)v\left(s\right),w\left(s\right)\rangle \text{d}s}\\ \le 2L_1{\Vert v\left(s\right)\Vert }_{L^{\infty }\left(\Omega \right)}{\displaystyle {\int }_0^t\left|\langle \left|\nabla w\left(s\right)\right|,w\left(s\right)\rangle \right|\text{d}s}\\ \le L_1{\Vert v\left(s\right)\Vert }_{L^{\infty }\left(\Omega \right)}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\Omega }\left({\Vert \nabla w\left(s\right)\Vert }^2+{\Vert w\left(s\right)\Vert }^2\right)\text{d}x\text{d}s}}\\ \le C{\displaystyle {\int }_0^t{\Vert w\left(s\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2}\text{d}s.\end{array}$ (63)

回顾(61)，从(63)可推出

$-2{\displaystyle {\int }_0^t\langle \sigma \left(\nabla u\left(s\right)\right)u\left(s\right)-\sigma \left(\nabla v\left(s\right)\right)v\left(s\right),w\left(s\right)\rangle \text{d}s}\le C{\displaystyle {\int }_0^t{\Vert w\left(s\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2}\text{d}s.$ (64)

令 $\rho \left(s\right)={\Vert w\left(s\right)\Vert }_{H^{\alpha }\left(\Omega \right)}^2$，从(58)-(60)和(64)，我们有

$\rho \left(s\right)\le C{\displaystyle {\int }_0^t\rho }\left(s\right)\text{d}s.$ (65)

此时，应用Gronwall引理，我们有 $\rho \left(s\right)=0$，即 $w=0$。

基金项目

本文受国家自然科学基金项目(No.11271141)和重庆市科学技术委员会(cstc2018jcyjAX0787)资助。