地物演化的物理基础及地物空间的布尔代数结构

Physical Foundation of Geo-Object Evolution and Boolean Algebraic Construction of Geo-Object Space

摘要: 物质存在与空间和时间有不可分割的联系。在时间中存在的事物，必然在时间算子的作用下发生变化，这种变化具有普遍性。A的闭集为A^-，它的幂集为P(A^-)，也即由A^-的所有子集所组成的集合。根据幂集对任意子集的包含关系，则(P(A^-),∪,∩,¯,Ø,A^-是布尔代数。对拓扑空间X上的基本点集α_i和结构点集e_i经布尔代数运算必得结果C_i∈Y，根据α_i和e_i的不同取值和关系，可对新生、消亡、扩大、缩小、分割、合并等多种变换子给出定义，从而揭示地物演化的数学原理。

Abstract: The existence of matter is inextricably connected with space and time. Things that exist in time must change under the action of time operators, and this change is universal. Closed set of A is the A^- and its power set is P(A^-) , meaning the set constituted by the all subset of A^-. According to the inclusion relation of power set for any subset, obtain that (P(A^-),∪,∩,¯,Ø,A^- is Boolean algebra. The based α_i and cstructed point set e_i on tpological space X by Boolean Algebraic operation must get the result of C_i∈Y, where  C_i shows the change of  . According to the value and relation of  α_i and e_i , many kinds of transforms such as new formation, extinction, expansion, reduction, division and merging, can be defined, so as to reveal the mathematical principle of geo-object evolution.

1. 引言

人类是地球的主人，人类要创造和维持最适合自身生存和可持续发展的环境，长期以来都十分重视人地关系。人是生物圈中最为积极和活跃的群体，人在自身进化的同时也改变了自然环境 [1]。世界各国对环境问题已在多个领域形成共识，如对二氧化碳排放量的控制，对生态环境的修复与保护，对环境污染的防治等等，都会导致相关地域地类性质和空间分布的改变。这种地类变更和空间结构的改变，有基于物理基础的自然原因 [2]，更多的是根据人类主体意图有目地的改造世界的行为 [3] [4]。地图是人类认识世界的工具，也是人类改变世界的成果 [5]。在用户需求多样化的数字时代，把地图广义地定义为标准地图和准地图的总和似乎更为合理 [6]。地图滞后反映的规律表明，任何地图的现势性恒小于1 [7] [8]。地图是地球表面的地物和现象的缩小模型，地图表示来源于实地，从地图反演实地，就能展现实地的变化。在我们生活的地球上，一切宏观尺度的地物变化，无处不在。房屋的拆迁与修建，铁路、公路、桥梁等基础设施的兴建，水利的兴修，矿山的开采，庄稼的种植与收割，火山、地震、泥石流、洪水灾害等，种种基于人类意识行为的规划实施或者突发的自然灾害，都会导致相关地域的地物的新生或消失，并不断地改变着地类的性质和空间分布结构格局。鉴于地物演化的普遍性和了解演化，掌握变化对人类自身生存和可持续发展的重要性和必要性，本文对地物演化的物理基础及地物空间的布尔代数结构，以及从 $S_1\to S_2$ 状态的演化模型进行研究和探讨。

2. 物质存在的时空特性

2.1. 空间和时间的产生

关于宇宙创生和时间、空间的出现问题，或许可从大爆炸宇宙学中寻找。根据广义相对论，爱因斯坦发现最简单的方程式要求宇宙膨胀。20世纪初的20年里，斯里夫尔(V·Slipher)在劳威尔天文台曾仔细研究过星系的光谱，发现光谱有红移现象，用多普勒效应解释即星系在退行。1929年，哈勃发现，在大尺度上，星系的退行速度与它们离开我们的距离成正比，越远的星系退行越快。这一正比关系称为哈勃定律。哈勃定律证明宇宙在膨胀，据此可推断过去星系之间的距离必定比现在小，宇宙密度更大，温度更高。最终，宇宙中的一切——空间、时间、物质和能量聚会到一个密度无穷大、体积为零的奇点。1970年，彭罗斯和史蒂芬·霍金在爱因斯坦广义相对论的基础上，证明了著名的奇性定理，确定宇宙在时间上必须有个开端，即140亿年前的宇宙大爆炸 [9]。2008年3月，美国科学家在对“威尔金森微波各向异性探测器”(WMAP)传回的观测数据进行分析和计算后，计算出了迄今最为精确的宇宙实际年龄，约为137.3亿年，并宣称这个数据正负误差不超过1.2亿年 [10]。在宇宙大爆炸后的10⁻⁴³ s时，时间、空间、真空场、引力出现 [11]。科学家们更愿意称此时为 $t=0$ 时刻 [12]。由于有星系红移或宇宙膨胀、3K宇宙背景辐射及氘和氦的丰度等观测事实的支持，大爆炸宇宙标准模型已被大多数科学家承认 [13]。

2.2. 物质存在的时空特性

空间和时间是物质固有的存在形式。时间是物质运动的连续性、间断性和延续性。时间是天体及其物体的自然属性 [14]。以地球自转为基础的时间计量系统称为恒星时，地球自西向东旋转一周所需的时间叫做一日，以某恒星确定旋转周期的，称为恒星日。一个恒星日分为24个恒星时，一恒星时分为60个恒星分，一恒星分又分为60恒星秒 [15]。现代科学界定义1秒为与铯—133原子能级发生的特定量子变化相对应的电磁辐射振动9,192,631,770次的时间长度 [16]。地球自转的方向不会改变，因此时间只有日复一日地向前而不可能倒退，所以时间是不可逆的一维性质。空间是物质的广延性和伸张性，是一切物质系统中各个要素的共存和相互作用的标志。空间、时间与运动着的物质的不可分离性已被狭义相对论证明和科学界公认。1908年，德国数学家闵可夫斯基(Minkowsky)为狭义相对论的四维时空提供了数学框架，即闵可夫斯基几何。此时时间和空间的坐标满足：

$l^2=x^2+y^2+z^2-t^2$ (1)

(1)式是人们为光速运动物体所在空间和时间建立的一个几何模型 [17]。

闵可夫斯基用四维时空对物理世界的解释，则更为深入浅出。闵可夫斯基称之为“世界”的四维连续区，是用“坐标” $x,y,z,t$ 来描述的，他把代表某一事件的点称为“世界点”。这样，按照物理学的说法，三维空间中的“事件”就成为四维“世界”的“存在”。三维空间中的“事件”与四维时空的等价性质，本身就表达了物质空间存在与时间的不可分割性。为了便于推理，设 $a_i$ 为性质为i的事件， $a_i$ 在三维空间的存在性，表现为其空间广延性和形状特征等，与三维空间坐标密切相关，因此， $a_i=f\left(x_i,y_i,z_i\right)$，物质的空间存在与时间的不可分割性表明：任何空间存在物都有它存在的时间——寿命。极限的空间长度是普朗克长度，即1.6 × 10⁻³⁵ m，小于普朗克长度，现有的空间概念不再适用；极限的时间间隔是普朗克时间间隔，约5.4 × 10⁻⁴⁴ s，小于普朗克时间间隔，现有的时间概念不再适用 [18] [19]，光速与普朗克时间间隔的乘积即为普朗克长度。1964年美国科学家盖尔曼提出强子不是基本粒子，而是由更基本粒子——夸克组成的观点。质子和中子的高速碰撞获得夸克的实验，证明了盖尔曼观点的正确。如今科学界已认同宇宙中存在6种不同类型的夸克。夸克的空间尺度小于10⁻¹⁶ m，而质子和中子则在10⁻¹⁶~10⁻¹⁵ m之间。华裔科学家丁肇中在实验中测出电子直径至少是少于10⁻¹⁹ m。这一切都表明，构成宇宙中一切物质的基本粒子，其空间尺度也都远大于空间概念适用的普朗克长度 [20]。四维时空的关系表明，在空间中存在的物质都有对应的存在时间——寿命。 $z^0$ 粒子可谓是寿命最短的粒子，它的寿命也有10⁻²⁵ s，这个数值也远大于时间概念适用的普朗克时间间隔5.4 × 10⁻⁴⁴ s。这一系列的事实说明，物质存在的充要条件是空间非空性和寿命为非零实值 [21] [22] [23]。对此，可用谓词公式表达物质在四维时空中存在概念：

[定义1] 三维空间中的事件设K为三维空间， $a_i$ 为性质为i的事件， $d_0=1.62\times {10}^{-35}\text{m}$ 为普朗克长度， $s_0=5.39\times {10}^{-44}\text{s}$ 为普朗克时间间隔，则：

$\forall \left(x_i,y_i,z_i\right)\in a_i\in K$，如果 $x_i>d_0\vee y_0>d_0\vee z_0>d_0\Rightarrow a_i\ne \varnothing$

$\Rightarrow t_i>s_0\iff \exists a_i\subset K$ (2)

(2)式表明，三维空间中的事物 $a_i$ 的存在导致 $t_i>d_0$ 的必然结果，从而阐明了物质的存在与时间的不可分割性。

从[定义1]又可推论：

[定义2] 任何空集的时间存在均为零

$\forall \left(x_i,y_i,z_i\right)\in a_i$，若 $x_i=0\wedge y_i=0\wedge z_i=0$

$\Rightarrow a_i=\varnothing \Rightarrow t_i=0$ (3)

(3)式表达了这样一个事实：现实中不存在的任何事物，它的寿命恒为零。

3. 地物演化的物理基础及地物演化的普遍性

三维空间中存在的一切事物都有各自的寿命，从该事物的创生时刻到消亡时刻的时间长度构成其寿命，记为 $t_i$。对于宇观事物，如宇宙及其包含的星系、恒星、行星等天体，有些虽然未能确定未来的消亡时刻，但其创生时刻却已被大量证据所确定。例如，根据出露在地球上最古老的岩石年龄，放射性同位素的衰变原理等测定，地球的年龄为46 × 10⁸年已得到公认。这就是说，地球诞生于46 × 10⁸年前。根据地球演化史可将地球分为3个最高级别的地质年代单位：太古宙、元古宙和显生宙。在显生宙中，根据生物界的总体面貌又可划分出3个二级地质年代单位：古生代、中生代和新生代 [24]。现代海洋和大陆的空间分布格局，实际上是发生在中生代以后的事件 [25]。有关研究表明，全球大洋岩石圈的总面积近3亿km²，它的年龄不超过1.5亿年，每年通过扩张而新生的洋底将近2 km²，这也意味着每年大约有约2 km²的地球表面消失，这是地物演化空间恒定性规律所决定的 [26] [27]。既然宇宙的年龄也只有137.3亿年，那么不难推定，宇宙间的一切事物，其寿命绝对小于宇宙的年龄。而任何事物在时轴上总有其创生时刻和消亡时刻，这两个时刻的间隔就是它的寿命，也只在其寿命期内被确认它的空间存在。事物的空间存在与时间的相关性得 $a_i=f\left(t\right)|t\in t_i$ 的结论，这样，从空集到非空集再到空集的演化，就成了一切空间存在物在时间中演化的模式：

$a_i=\varnothing \to a_i=f\left(t\right)\ne \varnothing \to a_i=\varnothing |t\in t_i$ (4)

(4)式表达了一切事物从创生到三维空间存在再到消亡的生存规律。一个人的出生，成长，死亡：一座房子从兴建，建成使用到基于种种原因的拆除等等。有些存在物，特别是有生命的存在物，在它的生命期内具有连续演化的特点，而每一时刻的存在的空间特性(广延性等)都是时间的函数。一个人，一栋房子，一个城市，一个国家，整个地球，太阳系，银河系乃至整个宇宙，都属于系统的范畴。任何系统都是作为过程而展开的，包括系统的发生过程、发育过程、相变过程、老化过程、消亡过程等。过程是在时间维中展开的。时间是一种算子，它以一切事物为运算对象，一切事物都会在时间算子作用下发生变化 [28]。在三维空间中存在的制图区域及其包含的各种地物，也同时存在于时间之中，因此，不可避免地会在时间算子作用下发生变化。(4)式就表达了地物创生－在四维时空中存在和演化这－最终必定在某一时刻消亡的普遍性原理。

4. 确定区域内地物的布尔代数结构

4.1. 基于幂集的布尔代数结构论证

[定理1] 亚当曲线设J是平面 $Y\subset R^2$ 上的点集，它是圆周的同胚像(称为约当闭曲线)，则 $Y-J$ 必由两个连通分支组成，以作为它们的共同边界 [29]。

由于方形、矩形、梯形等闭合线和任意约当曲线都同胚，它们也同约当曲线一样，把平面分为两个连通分支，即界线的内部 $A^{\circ }$ 和外部 $A^e$，就点集性质而论，内部和外部都为开集，而边界线则为闭集。设 $b\left(A\right)$ 为A的边界，则 $A^{-}=A^{\circ }\cup b\left(A\right)$ 就是A的闭包，也即包含的最小闭集 [30]。对于任意的 $A_i\in A|i\in I_A$，每个 $A_i$ 都有边界 $b\left(A_i\right)$，而且总有某些 $A_i$ 的边界与A的边界重合，即：

$\forall b\left(A_i\right),\exists b\left(A_i\right)\in b\left(A\right)|i\in I_A$ (5)

根据库拉托夫斯基闭包公理，可知所有 $A_i$ 的闭包的并集等于A的闭包：

$A^{-}={\cup }_{i\in I_A}{A}_i^{-}$ (6)

(6)式表明，A的闭包与各地类 $A_i$ 的闭包 $A_i^{-}$ 之间具有包含关系，即：

$A_i^{-}\subset A^{-}|i\in I_A$ (7)

[定义3] 幂集设A是集合，由A的所有子集所组成的集合称为A的幂集，记为 $P\left(A\right)$。即：

$P\left(A\right)=\left\{X|X\subseteq A\right\}$ (8)

根据(7)式给出的包含关系代入(8)式，得：

$p\left(A^{-}\right)=\left\{A_i^{-}|A_i^{-}\subseteq A^{-}\right\}$ (9)

由定义可知， $\varnothing \in P\left(A^{-}\right);A^{-}\in P\left(A^{-}\right);A_i^{-}\in P\left(A^{-}\right)$ 当且仅当 $A_i^{-}\subseteq A^{-}$。如果 $A^{-}$ 中有n个元素，则 $P\left(A^{-}\right)$ 中有 $2^n$ 个元素 [31]。

由于 $A^{-}$ 是非空集合，则 $\left(P\left(A^{-}\right),\cup ,\cap {,}^{-},\varnothing ,A^{-}\right)$ 是布尔代数 [32]。

地图的点集模型、符号模型和图层数据库模型都属于布尔代数系，从模型与原型的一一对应性条件可见，作为地图制作原型的实地，无疑也具有布尔代数结构 [33] [34] [35]。

4.2. 基于拓扑变换的布尔代数算子

[定义4] 拓扑变换(同胚)设X和Y是两个随意的拓扑空间，并设 $f:X\to Y$。如果f是连续双一一函数，并且它是反函数 $f^{-1}$ 也是连续的，f就叫做空间X到空间Y上的一个同胚或拓扑映射或拓扑变换。

地物的变化主要体现为某类性质的点集的新生或消亡、选取或舍弃、增补、扩大或缩小、移位、合并、分割等的变换，这些变换都属于满足特定条件下的拓扑变换。据此，可定义各个引发地类变化的布尔代数算子 [36] [37]：

[定义5] 基于基本点集和结构点集运算的目标点集。

设 $a_i,e_i\in X|e_i\subseteq a_i\vee e_i\not\subset a_i$，则称 $a_i$ 为基本点集， $e_i$ 为结构点集。在变换f下的象 $c_i=f\left(a_i,e_i\right)\in Y$ 称为目标点集。 $a_i$ 和 $e_i$ 的关系及变换f决定着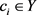的结果。

在[定义5]的基础上可对若干主要变换概念进行定义。

[定义6] 新生设 $a_i\in X$， $c_i\in Y$，在 $P\left(x,y,z\right)\in a_i\vee c_i$，若变换满足：

$\exists a_i=\varnothing \wedge e_i\ne \varnothing \Rightarrow c_i=f_1\left(\varnothing \cup e_i\right)=e_i\in Y$ (10)

则称 $c_i$ 为新生，即某一地点 $P\left(x,y,z\right)$ 上由空集到非空集的变换。 $i\in I_A$ 的任意性使在 $P\left(x,y,z\right)$ 点上可以新生任意性质的地物。

[定义7] 消亡设 $a_i\in X$， $c_i\in Y$， $P\left(x,y,z\right)\in a_i\vee c_i$，若变换满足：

$\exists a_i\ne \varnothing \wedge e_i=\varnothing \Rightarrow c_i=f_2\left(a_i\cap \varnothing \right)=\varnothing \in Y$ (11)

则称 $c_i$ 为 $a_i$ 的消亡。同理， $i\in I_A$ 的任意性使在 $P\left(x,y,z\right)\in a_i$ 上任何性质的地物都存在消亡的可能。

新生和消亡互为逆变换，即：

$f_1^{-1}=f_2\vee f_2^{-1}=f_1$ (12)

[定义8] 增补若变换满足：

$\exists a_i\ne \varnothing \in X\wedge e_i\ne \varnothing \notin X\Rightarrow c_i=f_3\left(a_i\cup e_i\right)=\left(a_i\cup e_i\right)\in Y$ (13)

则称 $c_i=\left(a_i\cup e_i\right)\in Y$ 中的 $e_i$ 为在 $a_i$ 上的增补元素。

地图编绘中对现势地物的增补即属此列。

[定义9] 扩大若变换满足：

$\exists a_i,e_i\in X\Rightarrow c_i=f_4\left(a_i\cup e_i\right)=\left(a_i\cup e_i\right)\in Y|a_i\ne \varnothing ,e_i\ne \varnothing$ (14)

则称 $c_i\in Y$ 为 $a_i$ 的扩大。

[定义10] 缩小若变换满足：

$\exists a_i,e_i\in X\Rightarrow c_i=f_5\left(a_i-e_i\right)=\left(a_i-e_i\right)\in Y|a_i\ne \varnothing ,e_i\ne \varnothing$ (15)

则称 $a_i$ 与 $e_i$ 的差集 $c_i=\left(a_i-e_i\right)\in Y$ 为 $a_i$ 的缩小。

扩大与缩小变换互为逆变换，即：

$f_4^{-1}=f_5\vee f_5^{-1}=f_4$ (16)

例如，在修筑道路时，若把道路视为 $a_i$，则 $a_i$ 在不断扩大，而被道路覆盖的主要地类就不断缩小，其扩大和缩小的代数和恒为零。

[定义11] 选取与舍弃 $\exists a_i\ne \varnothing \wedge e_i\ne \varnothing$， $a_i,e_i\in X$，若变换满足：

$\exists a_i,e_i\in X\Rightarrow c_i=f_6\left(a_i\right)\cup f_7\left(e_i\cap \varnothing \right)=\left(a_i\cup \varnothing \right)=a_i\in Y|a_i\ne \varnothing ,e_i\ne \varnothing$ (17)

则称为对 $a_i$ 选取，而 $f_7=\left(e_i\cap \varnothing \right)=\varnothing$ 为对 $e_i$ 的舍弃。

选取与舍弃互为逆变换，即：

$f_6^{-1}=f_7\vee f_7^{-1}=f_6$ (18)

地图编绘中对地物的选取和舍弃属于此定义的应用。

[定义12] 合并若变换满足：

$\exists \left(a_i\coprod e_i\right)\in X\Rightarrow f_8\left(a_i\coprod e_i\right)=\left(a_i\cup e_i\right)=c_i\in Y|a_i\ne \varnothing \wedge e_i\ne \varnothing$ (19)

则称 $c_i=\left(a_i\cup e_i\right)\in Y$ 为对 $a_i$ 和 $e_i$ 的合并。合并即从分离并到并集的变换。

[定义13] 分割若变换满足：

$\exists \left(a_i\cup e_i\right)\in X\Rightarrow f_9\left(a_i\cup e_i\right)=\left(a_i\coprod e_i\right)=c_i\in Y|a_i\ne \varnothing \wedge e_i\ne \varnothing$ (20)

则称 $c_i=\left(a_i\coprod e_i\right)\in Y$ 为对 $a_i$ 和 $e_i$ 的分割。分割即从并集到分离并的变换。

合并和分割互为逆变换，即：

$f_8^{-1}=f_9\vee f_9^{-1}=f_8$ (21)

地图比例尺变换中街区的合并和分割最为常见。

[定义14] 无移位变换和移位设 $P_a\left(x,y,z\right)\in a_i$ 为 $a_i$ 的定位点(定位中心)，若变换满足：

$\exists P_a\in a_i\Rightarrow P_c=f_{10}\left(P_a\right),s.td\left(P_a,P_c\right)\ge 0$ (22)

1) 当 $d\left(P_a,P_c\right)=0$ $\iff$ 无移位变换。 $s.t$ 表示“使得”或“能使”。

2) 当 $d\left(P_a,P_c\right)=k>0$ $\iff$ 位移变换，k为位移值。

3) 当 $a_i$ 为线状地物 $\wedge l_a\in a_i$ 为 $a_i$ 的定位线时，无位移变换和移位满足：

$\forall P_a\in l_a\Rightarrow P_c=f_{10}\left(P_a\right)\in Y,s.td\left(P_a,P_c\right)=k$ (23)

在(23)式中，当且仅当 $k=0$ 时为无位移变换；当 $k>0$ 时，称 $c_i$ 为 $a_i$ 的移位，k为位移值。

例如，在某块地上挖一个池塘，原地块的定位中心与新挖池塘的中心是一致的，属无移位变换；把实地上的一条铁路和路边的一间房子表示到某种比例尺的地图上，由于半依比例的铁路在其路宽方向是非比例的，其路宽已占用了很多的实地空间，此时要表示路边的房子的相对关系，房子必须向外推移，这就造至了房子定位点的移位，铁路的定位中心线也需有一定量的移位。

[定义15] 地类性质变换设 $i_a\in a_i,i_c\in c_i$，若变换满足：

$\exists i_a\in a_i\Rightarrow i_c=f_{11}\left(i_a\right)\in c_i|i_a\ne i_c$ (24)

则称 $c_i$ 为 $a_i$ 的性质变换。

例如，在 $a_i$ 上原为草地( $i_a$ )，把它改种水稻( $i_c$ )，便属于地类性质变换。

5. 实例

图1中，设 $t_1$ 时刻的区域 $S_1$ 的地物类型和结构为：

$S_1=a_1\cup b_1\cup c_1\cup d_1\cup e_1$ (25)

到 $t_2$ 时刻时区域演化为 $S_2$，其地物类型和结构为：

$S_2=a_2\cup \left(b_{2-1}\coprod b_{2-2}\right)\cup \left(c_1-h_2\right)\cup \left(d_{2-1}\coprod d_{2-2}\right)\cup e_2\cup f_2\cup g_2\cup h_2\left(i_{2-1}\coprod i_{2-2}\right)\cup j_2$ (26)

在(26)式中，虽然 $c_2=c_1$ 为实地的连通集，但由于桥梁 $h_2$ 的出现，如果仍把河流作为连通集，就会使桥下的覆盖点集重复计量，因此这里要用差集 $\left(c_2-h_2\right)$。而在(25)式则无此情况。

设 $m_n\in S_1|n=1,2,\cdots$ 为 $q_i\in S_2|i\in I$ 的新生地物的覆盖， $m_n\in m_n\ne \varnothing \to \varnothing$ 的消亡型地物。而 $q_i\in S_2\in \varnothing \to q_i\ne \varnothing$ 的新生型地物， $q_i$ 的性质与对应的新生地物相同。相关地物的消亡与新生具有历时性和和渐进性。

在 $\left(t_2-t_1\right)$ 的时间进程中， $S_1$ 的各类地物经演化而得 $S_2$，其演化过程如下：

1) $\exists m_1\in b_1\wedge a_2\notin S_1\Rightarrow a_2=\left(m_1\cap \varnothing \right)\cup q_i\cup a_1\in S_2|q_i\ne \varnothing$，此乃(14)式之扩大变换；

2) $\exists m_2\in b_1\wedge i_{2-1}\notin S_1\Rightarrow q_i=i_{2-1}=\left(m_2\cap \varnothing \right)\cup i_{2-1}=i_{2-1}\in S_2$。这是在 $m_2$ 消亡的基础上的新生地物 $i_{2-1}$ ；

3) $\exists \left(b_1-a_2-i_{2-1}\right)=\left(b_{2-1}\coprod b_{2-2}\right)\in S_2$。 $i_{2-1}$ 的生成使原本为连通集的 $\left(b_1-a_2\right)$ 演化为分离并；

4) $c_2=\left(c_1-h_2\right)\in S_2|h_2\ne \varnothing$。因为桥梁 $h_2$ 下的河流虽然是连通的，但因桥梁的面积已归入 $S_2$，所以它覆盖的面积必须减去，所以表现为 $c_1$ 和 $h_2$ 的差集；

5) $\exists m_3\in e_1\wedge e_2\notin S_1\Rightarrow e_2=\left(e_1-m_3\right)\in S_2\wedge \exists m_3\to d_1\Rightarrow d_{1^{\prime }}=d_1\cup m_3$，这是原属于 $e_1$ 的 $m_3$ 的质变导致了缩小的 $c_2$ 出现并同时使 $d_1$ 扩大为 $d_{1^{\prime }}$ ；

6) $\exists m_4\in d_{1^{\prime }}\wedge g_2\notin S_1\Rightarrow q_i=\left(m_4\cap \varnothing \right)\cup g_2=g_2\in S_2$。 $g_2$ 的新生同时使 $d_{1^{\prime }}$ 缩小；

Figure 1. The schematic diagram of area geo-object evolution

图1. 区域地物演化示意图

7) $\exists m_5\in \left(d_{1^{\prime }}-g_2\right)\wedge j_2\notin S_1\Rightarrow q_i=\left(m_5\cap \varnothing \right)\cup j_2=j_2\in S_2$。从属于 $\left(d_{1^{\prime }}-g_2\right)$ 的 $m_5$ 的消亡使 $j_2$ 新生；

8) $\exists m_6\in \left(d_{1^{\prime }}-g_2-j_2\right)\wedge f_2\notin S_1\Rightarrow q_i=\left(m_6\cap \varnothing \right)\cup f_2=f_2\in S_2$。从属于 $\left(d_{1^{\prime }}-g_2-j_2\right)$ 的 $m_6$ 的消亡使 $f_2$ 新生；

9) $\exists m_7\in \left(d_{1^{\prime }}-f_2-g_2-j_2\right)\wedge i_{2-2}\notin S_1\Rightarrow q_i=\left(m_7\cap \varnothing \right)\cup i_{2-2}=i_{2-2}\in S_2$。 $m_7\in \left(d_{1^{\prime }}-f_2-g_2-j_2\right)$ 的消亡使 $i_{2-2}$ 新生；

10) $\left(d_{2-1}\coprod d_{2-2}\right)\notin S_1\Rightarrow \left(d_{2-1}\coprod d_{2-2}\right)=\left(d_{1^{\prime }}-f_2-g_2-i_{2-2}-j_2\right)\in S_2$。 $\left(d_{2-1}\coprod d_{2-2}\right)$ 的出现及其在量值上的关系；

11) $\exists h_2\notin S_1\wedge \exists h_2\in S_2\Rightarrow s.t.\left(i_{2-1}\coprod i_{2-2}\right)\to \left(i_{2-1}\cup h_2\cup i_{2-2}\right)\in S_2$。桥梁 $h_2$ 的架设使得河流两边原本分离的路段变成了连通路，这时 $h_2$ 的桥面也具有了公路的性质。

$S_1=S_2$ 体现了演化空间的恒定性。

由于地类代号的任意性，所以任何有限的从 $S_1$ 的地物空间结构状态到 $S_2$ 的地物空间结构状态的演化，都可通过有限的布尔运算来实现，都可用本模型对相关代号赋值后进行描述和解释。

6. 结语

空间和时间是物质固有的存在形式，爱因斯坦的狭义相对论已证明了物质存在与空间和时间的不可分割性。物质存在的充要条件是空间非空性和寿命为非零实值。时间是一种算子，一切事物都在时间算子作用下发生变化。地球表面上的任何有限区域内的多种地物，区域对其内部地物都具有包含关系。A的幂集 $P\left(A\right)$ 对A具有包含关系。当A用其闭包 $A^{-}$ 替代时，其对应的幂集为 $P\left(A^{-}\right)$，此时 $\left(P\left(A^{-}\right),\cup ,\cap {,}^{-},\varnothing ,A^{-}\right)$ 为布尔代数。基于拓扑空间X和Y之间具有拓扑变换f的关系，把X上的基本点集 $a_i$ 和结构点集 $e_i$ 经 $f\left(a_i,e_i\right)$ 变换后获得 $c_i\in Y$，根据 $a_i$ 和 $e_i$ 的取值和关系，可定义某类性质的点集的新生或消亡、选取或舍弃、增补、扩大或缩小、移位、合并、分割等的变换，从而提出了能对地物空间结构从 $S_1$ 状态到 $S_2$ 状态演化的数学模型。用基于代码表达的演化模型，阐释了本模型的应用。

基金项目

国家自然科学基金项目(41671459, 41661021, 41574009, 41871376)，广西自然科学基金项目(2014DD29090)，国家重点研发项目(2016YFC0502401)，广西自然科学基金创新团队项目(2016JJF150001)。

参考文献

NOTES

^*通讯作者。