1. 引言
空间网格结构因为跨度大、整体性好、自重轻,在工业建筑与公共建筑中得到普遍运用 [1]。焊接空心球节点是网架结构常用的节点形式之一 [2],该节点中钢管通常采用热轧的无缝钢管,而钢材在冶炼、轧制过程中,由于不均匀的冷却过程和组织结构的变化,可能出现较大的残余应力 [3]。
残余应力是轧件在轧制过程中产生的平衡于其内部的应力。实践证明,残余应力直接影响轧件的疲劳强度、抗应力腐蚀能力、尺寸稳定性和使用寿命 [4]。同时有研究表明,钢在热轧和冷轧过程中因不均匀塑性变形产生的残余应力最高分别可达到屈服强度的20%和70% [5] [6]。目前,型钢等金属材料的残余应力已被大量学者深入研究,但对于焊接空心球节点残余应力测试尚无文献记载。
早在20世纪30年代人们就开始研究各种测试残余应力的方法 [7]。1934年,小孔释放法测量残余应力由德国学者J. Mathar [8] 提出,根据钻孔是否钻通,小孔释放法又可分为通孔法和盲孔法。目前半无损的盲孔测量法在工程领域应用较多。之后由Soete和Vancromburgge [9] 发展完善并形成一种应用电阻应变仪测量的基本方法。残余应力直接由理论推导式得出。本文主要通过盲孔法对焊接空心球节点热轧无缝钢管焊趾附近以及远离焊趾处表面的残余应力进行测量,得到应力分布规律。
2. 焊接空心球节点设计
焊接空心球节点通常会通过构造设计来避免节点的受压失稳破坏,将节点的破坏形式主要转变成更易控制的强度破坏。而构造设计主要涉及到管径、球径和壁厚等,我国《空间网格结构技术规程》中提出了焊接空心球截面规格尺寸的相关规定。网架和双层网壳的空心球外径和壁厚之比在25~45之间;单层网架取20~35;空心球外径与钢管外径之比在2.4~3.0之间;空心球壁厚与主钢管壁厚之比在1.5~2.0之间;空心球壁厚不宜小于4 mm。因此本文最终取钢管外径为159 mm,壁厚为8 mm,取空心球外径为400 mm,壁厚为10 mm。焊接空心球节点材料均为Q235-B钢材且管–球采用对接焊缝,具体参数见表1,试件图详见图1。

Table 1. The table of cross plate welded hollow spherical
表1. 十字板焊接空心球节点试件表

Figure 1. Welded hollow ball test piece (mm)
图1. 焊接空心球试件(mm)
3. 焊接空心球节点残余应力测试
本次试验采用盲孔法测量残余应力,试验主要包括应变片的粘贴和钻孔测量两部分内容。试验用到的主要仪器ZS-ⅡA型钻孔装置、CM-1L-10型静态电阻应变仪、万用表等。
3.1. 测点的选择与布置
根据焊接空心球节点球面特性,并充分避免焊缝的影响,测量其残余应力时在钢管焊趾附近以及在焊趾上方400 mm处均匀布置测点,然后在残余应力较大处密布测点,即可得到较为精确的钢管表面残余应力分布曲线。当钻孔深度达到1.2倍孔径时(美国材料试验学会要求1.2 D),表面应力进一步释放是极小的,所测得的应变值将趋于稳定 [10]。本次试验沿管面和球面均匀布置8个测点,每个测点盲孔直径为1.5 mm,孔深2 mm。打孔顺序为①→⑤→⑦→③→②→⑥→④→⑧,具体如图2~4所示。

Figure 2. Physical drawing of steel pipe measuring point arrangement
图2. 钢管测点布置实物图

Figure 3. Top view of measuring point layout
图3. 测点布置俯视图

Figure 4. Front view of measuring point layout
图4. 测点布置正视图
3.2. 应变片的选择和粘贴
3.2.1. 应变片的选择
本试验选用由宁波江东耀南机电设备有限公司生产的单向电阻应变计BX120-2CA。应变片的相关参数见表2。
3.2.2. 应变片的粘贴
在本次试验中,测点处残余应力的主应力方向未知,所以应选用三向应变花并按照如图5粘贴。在粘贴时对试件表面进行打磨处理,保证应变花与试件表面接触良好。借助万用表监测应变花与试件表面绝缘后再连接静态电阻应变仪并调零。

Figure 5. Schematic diagram of three-way strain flower
图5. 三向应变花示意图
3.3. 测量步骤
盲孔法测量步骤主要由安装钻具对中、钻孔、检测电阻应变仪读数。在测点处稳定固定好钻孔台座,在塞入2 mm厚垫片后打开电钻开始垂直钻孔。待1~2分钟后测读应变仪读数。图6为试验过程。
 (a) 安装钻具
(a) 安装钻具  (b) 对中
(b) 对中  (c) 钻孔
(c) 钻孔  (d) 测点盲孔
(d) 测点盲孔
Figure 6. Specimen point drilling diagram
图6. 试件测点钻孔图
4. 残余应力的计算、分布与结果分析
4.1. 盲孔法测定残余应力的原理
钻盲孔的目的是将构件内由于轧制、冷弯过程等因素产生的残余应力场和残余应变场释放,原来盲孔处处于平衡的应力场失去平衡,使盲孔附近产生释放应变。随即原应力场重新达到平衡,测量出前后应变的变化量,称之为释放应变,根据相关弹性力学原理 [11] 即可推算出盲孔处(测点)初始的残余应力。
通常结构表面残余应力是平面应力状态,两向主应力及主应力方向角均未知。所以需采用三向应变花进行测量。三向应变花测量得到钻孔前后的应变值
、 、
。
、
。
通过数学公式推导(将弹性模量E整合到应变释放系数A、B中),以应变反推应力 [12] [13],得到:
(1)
式中:
—应变花测量的应变值;
—主应力方向角;
A、B—应变释放系数;
—残余主应力。
得到残余主应力  后,即可通过弹性力学坐标变换得到测点处径向和环向残余应力,如式(2):
后,即可通过弹性力学坐标变换得到测点处径向和环向残余应力,如式(2):
(2)
式中:
—径向应力;
—环向应力。
4.2. 应变释放系数A、B的计算
本次试验被测构件材料为Q235B钢材,其材料性质为:
弹性模量
。
泊松比
。
三向应变花的计算图示 [14] 如图7所示。
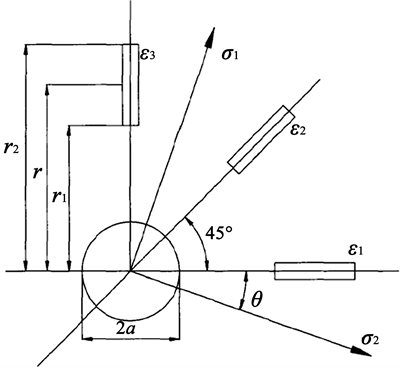
Figure 7. Blind-hole method strain flowers calculation diagram
图7. 盲孔法应变花计算简图
d—小孔孔径,mm;
r—孔中心到应变片敏感栅轴线中心距离,mm;
r1—孔中心到应变片敏感栅近端距离,mm;
r2—孔中心到应变片敏感栅远端距离,mm;
本试验中,d取1.5 mm,r取4.0 mm,r1取3.0 mm,r2取5.0 mm。
本文的应变释放系数的计算方法 [15] [16] 主要用基于通孔应变释放系数的Kirsch理论解,考虑了应变片尺寸。Kirsch理论解适用于通孔情况下的应变释放系数的计算,如式(3):
(3)
对于盲孔法,根据圣维南原理可知,在孔径d一定的条件下,孔深h增加,当h/d介于1.0~1.5时,释放应变基本保持不变,应变释放系数与通孔的Kirsch理论解接近。本试验h/d等于1.33,所以可近似使用Kirsch理论解计算,代入试验数据得:
。
4.3. 残余应力计算结果及塑性修正
根据式(1)、(2)和(3)对三个焊接空心球节点轧制钢管处残余应力进行计算,结果见表3~8。在钻孔过程中,孔周也会产生应力集中现象。规范规定 [17],当构件内部残余应力的数值超过材料屈服强度的60%以上,即进入塑性阶段。这时,由于钻孔而产生的释放应变就包含塑性应变,不能通过弹性理论计算,所以要对计算结果进行塑性修正。Scara-Mangas等人研究总结了基于弹性理论下对计算应力进行修正的经验公式 [18] [19],式(4)。
(4)
式中:
—塑性修正后的应力大小;
—计算应力;
 —钢材的屈服强度。
—钢材的屈服强度。
当
时,可采用式(4)对计算残余应力进行塑性修正。
本试验所采用的三个焊接空心球节点钢材为Q235-B,实测屈服强度
,对计算焊接残余应力超过材料屈服强度65%以上的结果进行塑形修正后,结果如下:
(1) 对构件KQ6-3远离焊趾处进行塑性修正后测量结果见下表3所示。

Table 3. KQ6-3 residual stress plastic correction calculation table far away from toe
表3. KQ6-3远离焊趾处残余应力塑性修正计算表
注:加“*”的孔号为测量残余应力超过屈服强度的65%,需要进行塑性修正。
对修正后的径向残余应力分析可知:最大径向拉应力为⑤号测点,达到401.2 MPa,超过了钢材屈服强度的45.9%;但此构件远离焊趾处并未检测到径向残余压应力。对修正后的环向残余应力分析可知:最大环向拉应力为⑤号测点,达到242.8 MPa,达到了钢材屈服强度的88.3%;最大环向压应力为①号测点,达到10.1 MPa,达到了钢材屈服强度的3.7%。
(2) 对构件KQ6-3焊趾处进行塑性修正后测量结果见下表4所示。


Table 4. KQ6-3 calculation table for plastic correction of residual stress at weld toe
表4. KQ6-3 焊趾处残余应力塑性修正计算表
注:加“*”的孔号为测量残余应力超过屈服强度的65%,需要进行塑性修正。
对修正后的径向残余应力分析可知:此构件焊趾处并未检测到径向残余拉应力;最大径向压应力为④号测点,达到159.8 MPa,达到了钢材屈服强度的58.1%。对修正后的环向残余应力分析可知:此构件焊趾处并未检测到环向残余拉应力;最大环向压应力为①号测点,达到299.8 MPa,超过了钢材屈服强度的9.0%。
(3) 对构件KQ6-4远离焊趾处进行塑性修正后测量结果见下表5所示。

Table 5. KQ6-4 residual stress plastic correction calculation table far away from toe
表5. KQ6-4远离焊趾处残余应力塑性修正计算表
注:加“*”的孔号为测量残余应力超过屈服强度的65%,需要进行塑性修正。
对修正后的径向残余应力分析可知:最大径向拉应力为①号测点,达到217.4 MPa,达到了钢材屈服强度的79.1%;最大径向压应力为⑥号测点,达到17.7 MPa,达到了钢材屈服强度的6.4%。对修正后的环向残余应力分析可知:最大环向拉应力为①号测点,达到145.8 MPa,达到了钢材屈服强度的53.0%;最大环向压应力为⑥号测点,达到45.4 MPa,达到了钢材屈服强度的16.5%。
(4) 对构件KQ6-4焊趾处进行塑性修正后测量结果见下表6所示。


Table 6. KQ6-4 calculation table for plastic correction of residual stress at weld toe
表6. KQ6-4焊趾处残余应力塑性修正计算表
注:加“*”的孔号为测量残余应力超过屈服强度的65%,需要进行塑性修正。
对修正后的径向残余应力分析可知:最大径向拉应力为⑧号测点,达到74.1 MPa,达到了钢材屈服强度的26.9%;最大径向压应力为③号测点,达到179.5 MPa,达到了钢材屈服强度的65.3%。对修正后的环向残余应力分析可知:此构件焊趾处并未检测到环向残余拉应力;最大环向压应力为③号测点,达到348.2 MPa,超到了钢材屈服强度的26.6%。
(5) 对构件KQ6-5远离焊趾处进行塑性修正后测量结果见下表7所示。

Table 7. KQ6-5 residual stress plastic correction calculation table far away from toe
表7. KQ6-5远离焊趾处残余应力塑性修正计算表
注:加“*”的孔号为测量残余应力超过屈服强度的65%,需要进行塑性修正。
对修正后的径向残余应力分析可知:最大径向拉应力为⑥号测点,达到400.8 MPa,超过了钢材屈服强度的45.7%;最大径向压应力为⑤号测点,达到35.7 MPa,达到了钢材屈服强度的13.0%。对修正后的环向残余应力分析可知:最大环向拉应力为⑥号测点,达到325.5 MPa,超过了钢材屈服强度的18.4%;最大环向压应力为⑤号测点,达到145.2 MPa,达到了钢材屈服强度的52.8%。
(6) 对构件KQ6-5焊趾处进行塑性修正后测量结果见下表8所示。


Table 8. KQ6-5 calculation table for plastic correction of residual stress at weld toe
表8. KQ6-5焊趾处残余应力塑性修正计算表
注:加“*”的孔号为测量残余应力超过屈服强度的65%,需要进行塑性修正。
对修正后的径向残余应力分析可知:最大径向拉应力为⑧号测点,达到361.6 MPa,超过了钢材屈服强度的31.5%;最大径向压应力为③号测点,达到278.0 MPa,超过了钢材屈服强度的1.1%。对修正后的环向残余应力分析可知:此构件焊趾处并未检测到环向残余拉应力;最大环向压应力为⑥号测点,达到462.9 MPa,超过了钢材屈服强度的68.3%。
4.4. 残余应力曲线及球面应力分布图
焊接空心球试件塑性修正后的残余应力曲线以及残余应力球面分布图如下。
(1) 构件KQ6-3远离焊趾处
KQ6-3远离焊趾处残余应力曲线图及球面分布图见图8、图9。

Figure 8. KQ6-3 residual stress curve away from weld toe
图8. KQ6-3远离焊趾处残余应力曲线图

Figure 9. KQ6-3 radial and hoop residual stress spherical distribution diagram away from the welding toe
图9. KQ6-3远离焊趾处径向、环向残余应力球面分布图
(2) 构件KQ6-3焊趾处
KQ6-3焊趾处残余应力曲线图及球面分布图见图10、图11。

Figure 10. KQ6-3 curve of residual stress at weld toe
图10. KQ6-3焊趾处残余应力曲线图

Figure 11. KQ6-3 radial and hoop residual stress spherical distribution at the welding toe
图11. KQ6-3焊趾处径向、环向残余应力球面分布图
(3) 构件KQ6-4远离焊趾处
KQ6-4远离焊趾处残余应力曲线图及球面分布图见图12、图13。

Figure 12. KQ6-4 residual stress curve away from weld toe
图12. KQ6-4远离焊趾处残余应力曲线图
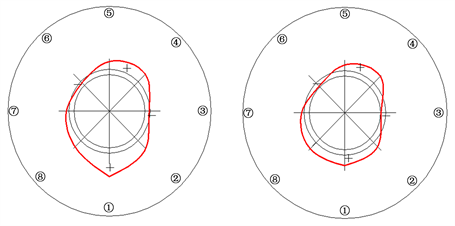
Figure 13. KQ6-4 spherical distribution of radial and hoop residual stress away from the welding toe
图13. KQ6-4远离焊趾处径向、环向残余应力球面分布图
(4) 构件KQ6-4焊趾处
KQ6-4焊趾处残余应力曲线图及球面分布图见图14、图15。

Figure 14. KQ6-4 curve of residual stress at weld toe
图14. KQ6-4焊趾处残余应力曲线图
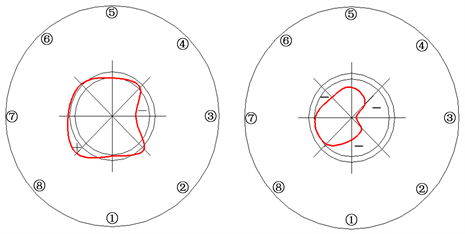
Figure 15. KQ6-4 radial and hoop residual stress spherical distribution at the welding toe
图15. KQ6-4焊趾处径向、环向残余应力球面分布图
(5) 构件KQ6-5远离焊趾处
KQ6-5远离焊趾处残余应力曲线图及球面分布图见图16、图17。

Figure 16. KQ6-5 residual stress curve away from weld toe
图16. KQ6-5远离焊趾处残余应力曲线图

Figure 17. KQ6-5 radial and hoop residual stress spherical distribution away from the welding toe
图17. KQ6-5远离焊趾处径向、环向残余应力球面分布图
(6) 构件KQ6-5焊趾处
KQ6-5焊趾处残余应力曲线图及球面分布图见图18、图19。

Figure 18. KQ6-5 curve of residual stress at weld toe
图18. KQ6-5焊趾处残余应力曲线图

Figure 19. KQ6-5 radial and hoop residual stress spherical distribution at the welding toe
图19. KQ6-5焊趾处径向、环向残余应力球面分布图
通过图8~19可知:
(1) 焊接空心球节点无缝钢管焊趾处和远离焊趾处的径向残余应力与环向残余应力的变化趋势大致相同,但是对于远离焊趾处径向残余应力略大于环向残余应力,对于焊趾处环向残余应力略大于径向残余应力;
(2) 由应力球面分布图也可看出两个位置的径向残余应力与环向残余应力沿球面分布形状大致相同;
(3) 由残余应力球面分布图可以看出,对于焊接空心球节点无缝钢管,远离焊趾处残余应力以拉应力为主,而焊趾处残余应力以压应力为主,数值均较大。
5. 结论
本文采用盲孔法对焊接空心球节点网架中热轧无缝钢管表面残余应力进行测试研究,得到如下结论:
(1) 焊接空心球节点远离焊趾处的残余拉应力值较大,压应力值较小。试验结果中部分测点处残余拉应力达到甚至超过母材屈服强度,最大残余拉应力可达到屈服强度的145.9%,而残余压应力最大才达到屈服强度的52.8%。在残余拉应力较大部位疲劳强度和抗拉强度较低,而焊接空心球节点常用于悬挂吊车的网架结构,并且该结构由于疲劳问题和弦杆受拉破坏问题产生的事故已有大量记载,因此,本研究对焊接空心球节点网架的研究有重要意义。
(2) 焊接空心球节点焊趾处的残余拉压应力值均较大,压应力分布居多。试验结果中部分测点处残余压应力达到甚至超过母材屈服强度,最大残余压应力可达到屈服强度的168.3%,而残余压应力最大可达到屈服强度的131.5%。这也验证了焊缝处残余应力较大的说法,并且较大的残余拉应力将对焊缝处的疲劳问题提供依据,较大压应力有可能引起受剪破坏从而导致起壳和压陷,因此,焊趾处的研究将为焊接空心球节点设计提供重大的参考依据。
(3) 采用盲孔法测量残余应力对工件的损伤较小,并且操作简单,结果较为可靠。
基金项目
国家自然科学基金(51578357)。
NOTES
*第一作者。
#通讯作者。