无穷维序列空间的线性n-宽度

Linear n-Width of Infinite-Dimensional Sequence Space

摘要: 本文讨论了无穷维序列空间的线性n-宽度，并估计其精确渐近阶。

Abstract: The linear n-width of infinite-dimensional sequence space is discussed in this paper, and its sharp asymptotic order is estimated.

1. 引言及主要结果

自1936年，A.N. Kolmogorov提出宽度以来，重要的函数类空间的n-宽度都得到比较深入的研究 [1] - [7]。而其方法基本都是将函数空间的n-宽度问题，转化为序列空间的宽度问题。因此，研究序列空间的宽度问题，有比较重要的意义。本文研究无穷维序列空间的宽度问题。

用 $l_p\left(1\le p\le \infty \right)$ 表示赋予范数 ${\Vert •\Vert }_p$ 的经典无序维实序列空间，其中 $x={\left\{x_k\right\}}_{k=1}^{\infty }$，

${\Vert x\Vert }_p=\{\begin{array}{l}{\left({\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\left|x_k\right|}^p}\right)}^{\frac{1}{p}},1\le p<\infty \\ \underset{k\ge 1}{\sup }\left|x_k\right|,p=\infty \end{array}$

众所周知， $l_p$ 空间界有以下性质：

1) 对 $1\le p<q\le \infty$，有 $l_p\subset l_q$，而 $l_q\not\subset l_p$ ；

2) 对 $1\le p<\infty$， ${\left\{e_k\right\}}_{k=1}^{\infty }$ 为 $l_p$ 的Schauder基。其中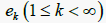， 表示第k个分量为1，其余分量为0的实序列。

对 ， $x=\left\{x_k\right\}\in l_p$， $r\in ℝ$，令

$x^{\left(r\right)}={\left\{k^r{x}_k\right\}}_{k=1}^{\infty },$

$l_{p,r}:=\left\{x\in l_p|x^{\left(r\right)}\in l_p\right\}.$

对 $x\in l_{p,r}$，记

${\Vert x\Vert }_{p,r}={\Vert x^{\left(r\right)}\Vert }_p$

易见， ${\Vert •\Vert }_{p,r}$ 为 $l_{p,r}$ 上的范数， $\left(l_{p,r},{\Vert •\Vert }_{p,r}\right)$ 为赋范线性空间，以下总把 $\left(l_{p,r},{\Vert •\Vert }_{p,r}\right)$ 简记为 $l_{p,r}$，用 $B_{p,r}$ 表示 $l_{p,r}$ 中的单位球。

对 $1\le q<p<\infty$，由Hȍlder不等式知，当 $r>\frac{1}{q}-\frac{1}{p}$ 时， $l_{p,r}\subset l_q$。本文讨论 $l_{p,r}$ 在

中的线性n-宽度，为此介绍线性n-宽度的定义。

定义1 设 $\left(X,\Vert •\Vert \right)$ 为赋范线性空间，A为X中非空子集， $n\in {\mathbb{N}}^{\ast }=\left\{0,1,2,\cdots \right\}$，称

${\lambda }_n\left(A,X\right):=\underset{T_n}{\inf }\underset{x\in A}{\sup }\Vert x-T_{n}x\Vert$

为A在X中的线性n-宽度，其中 $T_n$ 取遍从X到X上的秩不超过n的所有有界线性算子。

关于线性n-宽度的性质，可参阅Pinkus专著 [8]。

本文主要讨论 $l_{p,r}$ 在 $l_q\left(1\le q<p<\infty ,r>\frac{1}{q}-\frac{1}{p}\right)$ 中的线性n-宽度，并估计其精确阶，这也是本文的主要结果。

定理1 设 $1\le q<p<\infty$， $r>\frac{1}{q}-\frac{1}{p}$，，则

${\lambda }_n\left(B_{p,r},l_q\right)\succ \prec n^{-\left(r-\frac{1}{q}+\frac{1}{p}\right)}.$

其中，“ $\succ \prec$ ”定义如下： $c,c_i,i=0,1,\cdots$，表示仅与参数p，q，r相关的正常数。若对于正函数 $\mu \left(y\right)$ 和 $\nu \left(y\right)$， $y\in B$ (B是正函数 $\mu \left(y\right)$ 和 $\nu \left(y\right)$ 的定义域)，存在正常数 $c_1,c_2$，使得对任意的，有 $\mu \left(y\right)\ge c_1\nu \left(y\right)$ 或者 $\mu \left(y\right)\le c_1\nu \left(y\right)$，则将其记为： $\mu \left(y\right)\gg \nu \left(y\right)$ 或者 $\mu \left(y\right)\ll \nu \left(y\right)$。若存在正常数 $c_3,c_4$，使得对任意的 $y\in B$，有 $c_3\le \mu \left(y\right)/\nu \left(y\right)\le c_4$，则记为： $\mu \left(y\right)\succ \prec \nu \left(y\right)$，即对任意的 $y\in B$，若 $\mu \left(y\right)\gg \nu \left(y\right)$ 和 $\mu \left(y\right)\ll \nu \left(y\right)$ 同时成立，则有 $\mu \left(y\right)\succ \prec \nu \left(y\right)$。

2. 主要结果的证明

为证定理1，首先介绍有限维空间的线性n-宽度的相关结论。

$1\le p\le \infty$，用 $l_p^m$ 表示在 ${ℝ}^m$ 上赋予通常范数 ${\Vert •\Vert }_{l_p^m}$ 的Banach空间，其中

${\Vert x\Vert }_{l_p^m}=\{\begin{array}{l}{\left({\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\left|x_n\right|}^p}\right)}^{\frac{1}{p}},1\le p<\infty \\ \underset{1\le k\le m}{\max }\left|x_k\right|,p=\infty \end{array},x=\left(x_1,\cdots ,x_m\right)\in {ℝ}^m.$

用 $B_p^m$ 表示 $l_p^m$ 中的单位球。

易见， ${\left\{{e^{\prime }}_k\right\}}_{k=1}^m$ 为 $l_p^m$ 的基，其中 ${e^{\prime }}_k\in {ℝ}^m$ 表示第k个分量为1，其余分量为0的向量。

有限维空间 $l_p^m$ 的线性n-宽度有如下结果：

命理2 [8] 设 $1\le q<p\le \infty$， $n\in {\mathbb{N}}^{\ast }$，则

${\lambda }_n\left(B_p^m,l_q^m\right)=\{\begin{array}{l}{\left(m-n\right)}^{\frac{1}{q}-\frac{1}{p}},0\le n\le m,\\ 0,n>m.\end{array}$

下面，分别建立估计定理1上、下界的离散化空间。

对 $k\in \mathbb{N}=\left\{1,2,3,\cdots \right\}$，令

$S_k=\left\{n\in \mathbb{N}|2^{n-1}\le n<2^k\right\}.$

则 $m_k:=\left|S_k\right|=2^{k-1}$。

引理3 设 $1\le q<p<\infty$， $r>\frac{1}{q}-\frac{1}{p}$， $n\in {\mathbb{N}}^{\ast }$， ${\left\{n_k\right\}}_{k=1}^{\infty }$ 为非负整数序列，且 $n_k\le m_k$， ${\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{n}_k\le n}$，则

${\lambda }_n\left(B_{p,r},l_q\right)\ll {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{2}^{-rk}{\lambda }_{n_k}\left(B_p^{m_k},l_q^{m_k}\right)}.$

证明：对 $\forall k\in \mathbb{N}$，令

$F_k=span\left\{e_n|n\in S_k\right\}.$

易见 $F_k$ 为线性空间，且 $\dim F_k=m_k$。令

$I_k:F_k\to {ℝ}^{m_k}$

$x={\displaystyle \underset{j\in S_k}{\sum }{x}_j{e}_j\mapsto {\displaystyle \underset{j=1}{\overset{m_k}{\sum }}{x}_{2^{k-1}+j-1}{e^{\prime }}_j}}$

则 $I_k$ 为 $F_k$ 到 ${ℝ}^{m_k}$ 上的同构映射。

对 $\forall x={\displaystyle \underset{j\in S_k}{\sum }{x}_j{e}_j}\in F_k$， $\forall y={\displaystyle \underset{j\in S_k}{\sum }{y}_j{e}_j}\in F_k$，则

${\Vert x\Vert }_{p,r}={\left({\displaystyle \underset{j=2^{k-1}}{\overset{2^k-1}{\sum }}{\left|j^r{x}_j\right|}^p}\right)}^{\frac{1}{p}}\succ \prec 2^{kr}{\left({\displaystyle \underset{j=2^{k-1}}{\overset{2^k-1}{\sum }}{\left|x_j\right|}^p}\right)}^{\frac{1}{p}}=2^{kr}{\Vert I_{k}x\Vert }_{l_p^{m_k}},$ (1)

${\Vert y\Vert }_q={\Vert I_{k}y\Vert }_{l_q^{m_k}}.$ (2)

从而

${\lambda }_{n_k}\left(B_{p,r}\cap F_k,l_q\cap F_k\right)\ll 2^{-rk}{\lambda }_{n_k}\left(B_p^{m_k},l_q^{m_k}\right)$

因此

${\lambda }_n\left(B_{p,r},l_q\right)\le {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\lambda }_{n_k}\left(B_{p,r}\cap F_k,l_q\cap F_k\right)}\ll {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{2}^{-rk}{\lambda }_{n_k}\left(B_p^{m_k},l_q^{m_k}\right)}．$

引理3得证。

引理4 设 $1\le q<p<\infty$， $r>\frac{1}{q}-\frac{1}{p}$， $n\in {\mathbb{N}}^{\ast }$，记。令 $k=k^{\prime }+2$，则

${\lambda }_n\left(B_{p,r},l_q\right)\gg 2^{-r{k}^{\prime }}{\lambda }_n\left(B_p^{m_k},l_q^{m_k}\right)$

证明：易见 $m_k\ge n$，且由(1)、(2)可知

${\lambda }_n\left(B_{p,r},l_q\right)\ge {\lambda }_n\left(B_{p,r}\cap F_k,l_q\cap F_k\right)\ge 2^{-rk}{\lambda }_n\left(B_p^{m_k},l_q^{m_k}\right).$

3. 定理1的证明

3.1. 定理1上界的证明

令 $k^{\prime }=\left[{\log }_{2}n\right]+1$。对 $k\in \mathbb{N}$，令

$n_k=\{\begin{array}{l}{m}^k,1\le k\le k^{\prime }\\ \left[n{2}^{k^{\prime }-k}\right],k>k^{\prime }\end{array}$

则 ${\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{n}_k\le n}$，由引理3及命理2知

$\begin{array}{c}{\lambda }_n\left(B_{p,r},l_q\right)\ll {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{2}^{-rk}{\lambda }_{n_k}\left(B_p^{m_k},l_q^{m_k}\right)}={\displaystyle \underset{k=k^{\prime }}{\overset{\infty }{\sum }}{2}^{-rk}{\lambda }_{n_k}\left(B_p^{m_k},l_q^{m_k}\right)}\\ \le {\displaystyle \underset{k=k^{\prime }}{\overset{\infty }{\sum }}{2}^{-rk}{m}_k^{\frac{1}{q}-\frac{1}{p}}}\le {\displaystyle \underset{k=k^{\prime }}{\overset{\infty }{\sum }}{2}^{-rk}{2}^{\left(\frac{1}{q}-\frac{1}{p}\right)k}=}{\displaystyle \underset{k=k^{\prime }}{\sum }{2}^{-\left(r-\frac{1}{q}+\frac{1}{p}\right)k}}\\ \ll 2^{-\left(r-\frac{1}{q}+\frac{1}{p}\right)k^{\prime }}\ll n^{-\left(r-\frac{1}{q}+\frac{1}{p}\right)}\end{array}$

3.2. 定理1下界的证明

令 $k^{\prime }$ 与k为满足引理4的 $k^{\prime }$ 与k，则由引理4和命题1知

$\begin{array}{c}{\lambda }_n\left(B_{p,r},l_q\right)\gg 2^{-rk}{\lambda }_n\left(B_p^{m_k},l_q^{m_k}\right)\gg 2^{-r{k}^{\prime }}{\left(m_k,n\right)}^{\frac{1}{q}-\frac{1}{p}}\gg 2^{-rk}{\left(2^{k-1},2^{k^{\prime }}\right)}^{\frac{1}{q}-\frac{1}{p}}\\ \gg 2^{-r{k}^{\prime }}{2}^{\left(\frac{1}{q}-\frac{1}{p}\right)k^{\prime }}=2^{-\left(r-\frac{1}{q}+\frac{1}{p}\right)k^{\prime }}\gg n^{-\left(r-\frac{1}{q}+\frac{1}{p}\right)}\end{array}$

综上所述，定理1得证。