一类超混沌的Faraday圆盘发电机的Zero-Zero-Hopf分支

Zero-Zero-Hopf Bifurcation of a Hyperchaotic Faraday Disk Dynamo

摘要: 本文主要研究了一类四维的self-exciting Faraday圆盘发电机，它描述了azimuthal eddy流的作用。首先通过计算Lyapunov指数，发现该系统是一个超混沌的系统。然后研究了系统的zero-zero-Hopf分支。利用平均理论，获得了在zero-zero-Hopf分支点存在两个周期解的充分条件，并进一步讨论了周期解的稳定性。

Abstract: The paper investigates the bifurcation of periodic solutions at the zero-zero-Hopf equilibrium of a hyperchaotic Faraday disk dynamo. By means of the averaging theory, the paper obtains the suffi-cient conditions that two periodic solutions will appear at the bifurcation point and discusses the stability of the two orbits.

1. 引言

1996年，Hide等提出了一个self-exciting Faraday圆盘单极发电机，它是一个非线性的三维动力系统 [1]。在此基础上，逐渐发展了很多改进的模型 [2] - [10]，其中Hide和Moroz提出了一类四维的发电机，它描述了方位涡流(azimuthal eddy currents)的作用。其模型如下：

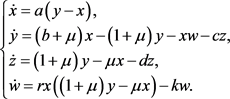(1.1)

其中x和y分别表示圆盘和线圈的磁通量，z表示电动机电枢的角转速，w表示圆盘的角转速。

Moroz在文献 [11] 中已经做了一些数值分析去研究系统(1.1)的zero-zero-Hopf分支，然而并没有严格的证明。本文将给出系统存在zero-zero-Hopf分支的证明，并把相应的周期解求出来。

一个zero-Hopf或zero-zero-Hopf奇点意味着可能出现混沌。近年来，虽有一些文献研究三维混沌系统的zero-Hopf分支 [12] [13] [14]，但由于高维系统的复杂性，对四维及以上系统的zero-zero-Hopf分支的研究非常少 [15]。Cid-Montiel等在文献 [15] 中研究了一个四维超混沌的Lorenz系统的zero-Hopf分支。Chen 等在文献 [16] 中研究了一个广义Lorenz-Stenflo超混沌系统zero-zero-Hopf分支。

2. 超混沌和zero-zero-Hopf分支

系统(1.1) 总有一个奇点 $E_0=\left(0,0,0,0\right)$。当 $\frac{k\left(bd-c-d\right)}{rd}>0$ 时，还有如下的两个奇点：

$E_{\pm }=\left(\pm x_1,\pm x_1,\pm \frac{x_1}{d},\frac{r{x}_1^2}{k}\right)$,

其中 $x_1=\sqrt{\frac{k\left(bd-c-d\right)}{rd}}$。

对初始值 $\left(0,0,0.2511,0\right)$ 和参数 $\left(a,b,c,d,k,r,\mu \right)=\left(16,60,15,0.1,1,6,0.5\right)$，我们计算出来Lyapunov指数是0.2927，0.1826，0，−19.0777。因此系统是超混沌的，图1显示了一个超混沌吸引因子。

图1是系统(1.1)的超混沌吸引因子，其中初始值 $\left(0,0,0.2511,0\right)$，参数 $\left(a,b,c,d,k,r,\mu \right)=\left(16,60,15,0.1,1,6,0.5\right)$。

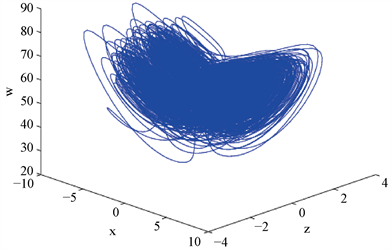
Figure 1. Hyperchaotic attraction factor of system (1.1)

图1. 系统(1.1)的超混沌吸引因子

下面我们应用平均理论去研究系统(1.1)的zero-zero-Hopf分支。当 $\mu \ne -a$，一些表达式过于庞大。为了表达的方便，我们令 $\mu =-a$。

理论1 对 $c=1-b,d=-1,k=0,b<0$，原点 $E_0$ 是系统(1.1)的一个zero-zero-Hopf奇点。在 $E_0$ 的特征值是0，0， $\pm \omega i$，其中 $\omega =\sqrt{-b}$。

证明. 在 $E_0$ 的特征方程是

$\begin{array}{l}{\lambda }^4+\left(k+1+d\right){\lambda }^3+\left(k+a+c+d+kd-ab-ac\right){\lambda }^2\\ +\left(ac+ad+ak+ck+kd-abd-abk-ack\right)\lambda -ka\left(kd-c-d\right)=0\end{array}$ (2.1)

当 $c=1-b,d=-1,k=0,b<0$ 时，(2.1)有根0，0， $\pm \omega i$，其中 $\omega =\sqrt{-b}$。

利用平均理论，我们能证明下面的定理。

理论2 令

$\begin{array}{l}\left(c,d,k\right)=\left(1-b+\epsilon c_1,-1+\epsilon d_1,\epsilon k_1\right),\rho =c_1+d_1-b{d}_1,\\ N={\rho }^2+2d_1\left(a+b-ab\right)\rho +d_1^2\left(b-1\right)\left(b{\left(a-1\right)}^2-a^2\right),\end{array}$

这里 $c_1{d}_1{k}_1\ne 0$。

假设 $aN\ne 0,k_1\rho r>0,b<0$，那么系统(1.1)有一个zero-zero-Hopf分支。当 $\epsilon >0$ 且 $\epsilon$ 足够小时，在 $E_0$ 产生两个周期解。如果 $d_1>0,k_1>0,a\rho <0,N>0$，那么这两个周期解是稳定的。

证明. 作变换

$c=1-b+\epsilon c_1,d=-1+\epsilon d_1,k=\epsilon k_1,$

系统(1.1)变成

$\{\begin{array}{l}\stackrel{\dot{}}{x}=a\left(y-x\right),\hfill \\ \stackrel{\dot{}}{y}=\left(b-a\right)x-\left(1-a\right)y+\left(b-1\right)z-xw-c_{1}z\epsilon ,\hfill \\ \stackrel{\dot{}}{z}=ax+\left(1-a\right)y+z-d_{1}z\epsilon ,\hfill \\ \stackrel{\dot{}}{w}=ra{x}^2+r\left(1-a\right)xy-k_{1}w\epsilon .\hfill \end{array}$ (2.2)

令 ${\left(x,y,z,w\right)}^{\text{T}}={\left(\epsilon u,\epsilon v,\epsilon p,\epsilon q\right)}^{\text{T}}$。我们把 ${\left(u,v,p,q\right)}^{\text{T}}$ 又表示为 $X={\left(x,y,z,w\right)}^{\text{T}}$，那么系统(2.2)变为

$\begin{array}{c}\stackrel{\dot{}}{X}=F_0\left(t,X\right)+\epsilon F_1\left(t,X\right)\\ =\left(\begin{array}{c}a\left(y-x\right)\\ \left(b-a\right)x+\left(a-1\right)y+\left(b-1\right)z\\ ax+\left(1-a\right)y+z\\ 0\end{array}\right)-\epsilon \left(\begin{array}{c}0\\ c_{1}z+xw\\ d_{1}z\\ k_{1}w-ra{x}^2+r\left(a-1\right)xy\end{array}\right).\end{array}$ (2.3)

下面利用平均理论来研究系统(2.2)的动力学行为。首先我们考虑下面这个未扰动系统的初值问题

$\stackrel{\dot{}}{X}=F_0\left(t,X\right),X_0=\left(x_0,y_0,z_0,w_0\right).$ (2.4)

系统(2.4)的解是 $X\left(t,X_0\right)=\left(x\left(t\right),y\left(t\right),z\left(t\right),w\left(t\right)\right)$，其中

$\begin{array}{l}m=\frac{b\left(1-a\right)x_0+a{y}_0+a\left(1-b\right)z_0}{b},\\ x\left(t\right)=\left(ab{x}_0-a{y}_0+a\left(b-1\right)z_0\right)\frac{\cos \left(\omega t\right)}{b}++\omega a\left(x_0-y_0\right)\frac{\sin \left(\omega t\right)}{b}+m,\end{array}$

$\begin{array}{l}y\left(t\right)=\left(b\left(a-1\right)x_0+\left(b-a\right)y_0+\left(b-1\right)a{z}_0\right)\frac{\cos \left(\omega t\right)}{b}+\left(\left(b-a\right)x_0+\left(a-1\right)y_0+\left(b-1\right)z_0\right)\frac{\sin \left(\omega t\right)}{\omega }+m,\\ z\left(t\right)=\left(b\left(1-a\right)x_0+a{y}_0+\left(a+b-ab\right)z_0\right)\frac{\cos \left(\omega t\right)}{b}+\left(a{x}_0+\left(1-a\right)y_0+z_0\right)\frac{\sin \left(\omega t\right)}{\omega }-m,\\ w\left(t\right)=w_0.\end{array}$

当 $X_0\ne 0$ 时，系统(2.4)的所有解 $X\left(t,X_0\right)$ 是周期的，其中周期为 $T=\frac{2\pi }{\omega }$。沿着一个周期解 $X\left(t,X_0\right)$，

其线性化系统 $\stackrel{\dot{}}{Y}=D_X{F}_0\left(t,X\left(t,X_0\right)\right)Y$ 的基解矩阵 $M_{X_0}\left(t\right)$ 是

$M_{X_0}\left(t\right)=\frac{1}{b}\left(\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& 0\\ a_{21}& a_{22}& a_{23}& 0\\ a_{31}& a_{32}& a_{33}& 0\\ 0& 0& 0& b\end{array}\right),$

其中

$\begin{array}{l}{a}_{11}=ab\cos \left(\omega t\right)+\omega a\sin \left(\omega t\right)+b\left(1-a\right),\\ a_{12}=-a\cos \left(\omega t\right)-\omega a\sin \left(\omega t\right)+a,\\ a_{13}=a\left(b-1\right)\left(\cos \left(\omega t\right)-1\right),\\ a_{21}=\left(a-1\right)b\cos \left(\omega t\right)+\omega \left(a-b\right)\sin \left(\omega t\right)+b\left(1-a\right),\\ a_{22}=\left(b-a\right)\cos \left(\omega t\right)+\omega \left(1-a\right)\sin \left(\omega t\right)+a,\end{array}$

$\begin{array}{l}{a}_{23}=\left(b-1\right)\left(a\cos \left(\omega t\right)-\omega \sin \left(\omega t\right)-a\right),\\ a_{31}=b\left(1-a\right)\cos \left(\omega t\right)-\omega a\sin \left(\omega t\right)-b\left(1-a\right),\\ a_{32}=a\cos \left(\omega t\right)-\omega \left(1-a\right)\sin \left(\omega t\right)-a,\\ a_{33}=\left(b+a-ab\right)\cos \left(\omega t\right)-\omega \sin \left(\omega t\right)+a\left(b-1\right).\end{array}$

计算积分

$G\left(X_0\right)=\frac{1}{T}{\displaystyle {\int }_0^T{M}_{X_0}^{-1}}\left(t\right)F_1\left(t,X\left(t,x_0\right)\right)\text{d}t=\frac{1}{2b^2}\left(G_1\left(X_0\right),G_2\left(X_0\right),G_3\left(X_0\right),G_4\left(X_0\right)\right),$

其中

$\begin{array}{l}{G}_1\left(X_0\right)=2ab\left(2a-1\right)x_0{w}_0-a^2\left(b+3\right)y_0{w}_0-3a^2\left(1-b\right)z_0{w}_0-\left(\left(4a-3\right)\rho +a{d}_1\left(b-1\right)\right)ab{x}_0\\ +\left(3a\rho +b{c}_1\left(a-1\right)\right)a{y}_0-a\left(\left(3ab-3a-b\right)\rho +c_{1}b\right)z_0,\\ G_2\left(X_0\right)=ab\left(4a-b-3\right)x_0{w}_0-a\left(ab+3a-2b\right)y_0{w}_0+a\left(b-1\right)\left(3a-b\right)z_0{w}_0\\ -b\left(a\left(3a-4\right)\rho +c_1\left(a^2-ab+b\right)\right)x_0+\left(\left(3a^2-ab+b\right)\rho +ab{c}_1\left(a-2\right)\right)y_0\\ +\left(b-1\right)\left(\left(ab-3a^2-b\right)\rho +b{d}_1\left(ab-2a-b\right)\right)z_0,\end{array}$

$\begin{array}{l}{G}_3\left(X_0\right)=ab\left(3-4a\right)x_0{w}_0+a\left(ab+3a-b\right)y_0{w}_0-3a^2\left(b-1\right)z_0{w}_0\\ +\left(4ab\rho \left(a-1\right)+b{d}_1\left(a^{2}b-a^2-b\right)\right)x_0-\left({\left(a-1\right)}^{2}b{c}_1+3a^2\rho +b{d}_1\right)y_0\\ -\left(\left(b-3a^{2}b+3a^2\right)\rho -2b{d}_1\left(ab-a-b\right)\right)z_0,\\ G_4\left(X_0\right)=br\left(3a^{2}b-a^2-4ab+2b\right)x_0^2-a^{2}r\left(b-3\right)y_0^2+3a^{2}r{\left(b-1\right)}^2{z}_0^2-4abr\left(a-1\right)x_0{y}_0\\ +2abr\left(b-1\right)\left(3a-2\right)x_0{z}_0-6a^{2}r\left(b-1\right)y_0{z}_0-2k_1{b}^2{w}_0\end{array}$

解方程 $G\left(X_0\right)=0$，我们得到下面的解

$\begin{array}{l}{S}_0=\left(0,0,0,0\right),\\ S_1=\left(\sqrt{\frac{k_1\rho }{r}},\sqrt{\frac{k_1\rho }{r}},-\sqrt{\frac{k_1\rho }{r}},\rho \right),\\ S_2=\left(-\sqrt{\frac{k_1\rho }{r}},-\sqrt{\frac{k_1\rho }{r}},\sqrt{\frac{k_1\rho }{r}},\rho \right).\end{array}$

$S_0$ 对应奇点 $E_0=\left(0,0,0,0\right)$。对其他两个解 $S_1$ 和 $S_2$，我们有

$G\left(S_1\right)=G\left(S_2\right)=0,$

$\det \left(\left(\partial G/\partial X_0\right)\left(S_1\right)\right)=\det \left(\left(\partial G/\partial X_0\right)\left(S_2\right)\right)=-\frac{a{k}_1\rho N}{2b^2}.$

因此根据平均理论，系统(2.3)存在的两个周期为T的解 $X_1\left(t,\epsilon \right)$ 和 $X_2\left(t,\epsilon \right)$，当时，有 $X_1\left(t,\epsilon \right)\to S_1$ 和 $X_2\left(t,\epsilon \right)\to S_2$。考虑到系统(2.2)和(2.3)的关系，系统(2.3)的两个周期解分别对应系统(2.2)的两个周期解 $\epsilon X_1\left(t,\epsilon \right)$ 和 $\epsilon X_2\left(t,\epsilon \right)$。

最后，我们计算Jacobian矩阵 $\left(\partial G/\partial X_0\right)\left(S_1\right)$ 和 $\left(\partial G/\partial X_0\right)\left(S_2\right)$ 的特征值来判断两个周期解的稳定性。对这两个矩阵而言，特征多项式是相同的，如下

$\left(b{\lambda }^2+k_{1}b\lambda +2a{k}_1\rho \right)\left(4b{\lambda }^2+4b{d}_1\lambda -N\right)=0.$ (2.5)

当 $d_1>0,k_1>0,a\rho <0,N>0$ 时，方程(2.5)的根都有负实部，这意味着在 $E_0$ 产生的两个周期解 $X_1\left(t,\epsilon \right)$ 和 $X_2\left(t,\epsilon \right)$ 是稳定的。

3. 结束语

通过选取适当的参数，我们计算发现系统有两个正的Lyapunov指数，是一个超混沌的系统。不同于前人的数值工作，本文对系统存在zero-zero-Hopf分支给出了严格的证明，并给出了周期解的表达式，以及周期解稳定的条件。

NOTES

^*通讯作者。