支持向量机分类理论中的几个细节理解及实验

Understanding of Theory and Experiments in Support Vector Machine Classification

摘要: 目前的大数据时代，机器学习作为数据处理的关键技术，不可缺少。各个高校在很多专业都在开展机器学习这门课程，其中的支持向量机算法作为重要内容之一，广受学生青睐。但在教学过程中，我们发现其理论在某些方面比较晦涩难懂，本文在简要概述完支持向量机分类的理论后，总结了几个关键细节的理解，比如：支持向量机线性分类器模型中的最大化Margin的理解；线性分类器模型中目标函数和约束条件的推导过程中某些知识点的理解；线性分类器模型求解过程中，为什么拉格朗日乘子大于0对应的数据点就是支持向量？支持向量机的分类面唯一吗？最后，给出了Matlab、R语言、python等几种软件在iris数据上的实验代码及实验中得到的支持向量机模型的获取方法。这些细节的理解及软件实验，对支持向量机模型都进行了透彻的剖析和融会贯通，有助于支持向量机分类学习中的初步探索和深入的研究，给广大支持向量机的学习者和使用者提供了重要的参考。

Abstract: In the era of big data, machine learning is indispensable for data processing. Various colleges and universities are carrying out the course of machine learning in many majors. As one of the im-portant contents, support vector machine algorithm is widely favored by students. But in the pro-cess of teaching, we find that its theory is rather obscure in some aspects. After summarizing the theory of support vector machine classification, this paper summarizes several key points’ under-standing, such as, the understanding of maximizing margin in support vector machine linear classi-fier model; the understanding of some knowledge points in the derivation of objective functions and constraints in linear classifier model; in the process of solving linear classifier model, why is the da-ta point corresponding to Lagrange multiplier greater than 0 support vector? Is the support vector machine classification face unique? Then, the experimental codes of several softwares such as MATLAB, R language and python on iris data and the understanding of relevant results are ex-pounded. The understanding of these details and the software experiment have carried on the thorough analysis and the fusion to the support vector machine model, which is helpful for the pre-liminary exploration and in-depth study of SVM classification learning, having provided the im-portant reference for the broad support vector machine learner and the user.

1. 支持向量机的基本理论框架

处在大数据的时代，从数据中挖掘各种信息和关联关系，机器学习方法在其中的应用显得非常重要。统计学习理论基础上发展起来的支持向量机(support vector machine, SVM)，有一套严实的统计学习理论作为支撑 [1]，是机器学习的重要算法之一，在处理有限样本的问题上很有优势，已经广泛应用于各行各业，比如：图像识别与分类、文本分类、股票预测、生物医学等等 [2] [3] [4] [5] [6]。其理论过程的一般形式如下面几个方面 [7] [8] [9] [10]，从这些知识点中，我们给出一些细节的精细理解。

1) SVM的线性分类器模型

一般，先从感知机的二分类问题进行引入。当感知机就一个神经元用于处理信息时，其结构图如图1。

当其中的激活函数f取符号函数sign时，设 $W={\left(w_1,w_2\right)}^{\text{T}}$， $x={\left(x_1,x_2\right)}^{\text{T}}$，则这个神经元处理完信息以后的输出是：

Figure 1. Information processing of a neuron

图1. 单神经元的信息处理情况

Figure 2. Binary classification problem

图2. 二分类问题

$o=sign\left(w_1\ast x_1+w_2\ast x_2+b\right)=sign\left(W^{\text{T}}x+b\right)$，其中 $sign\left(x\right)=\{\begin{array}{l}1,x>0\\ 0,x=0\\ -1,x<0\end{array}$。

这实际上相当于图2中的二分类问题，圆点数据点这一类对应输出是−1，三角数据点一类对应输出是1。也就相当于在两类样本点中间找一条直线把它们分开。这样的直线有很多，如下图3，支持向量机就是围绕着去寻找中间那条最好的直线而进行推导。二维空间里是分类线；三维空间里是分类平面；四维空间以上，则称为分类超平面，为了便于理解和观察，以下主要在二维空间上作图和进行阐述。

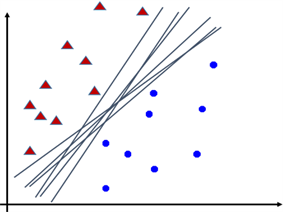
Figure 3. Classification lines in binary classification problem

图3. 二分类问题的多条分类直线

Figure 4. The best classification line in binary classification problem

图4. 二分类问题中最好的分类线情况

分类线距离哪一侧的样本点越远，那么这类样本点就被分类得更好，并且对于这类中新来的测试样本点也会被分得更好，从而具有更好的泛化性。两侧的样本点都按照这样的原则，那么就会出现图4的情形，中间那条分类线只能是距离两边最近的样本点都一样远，最近的样本点叫支持向量，并且过两边的支持向量分别作平行于分类线的直线，那么最好的分类线就是要使得过两边支持向量的平行线之间的距离最大，即图4中的ρ最大。这是从两条平行线的“函数间隔”来分析出ρ的最大化。那么，得到初步的线性分类器模型可以是这样：

$\begin{array}{l}\max \rho \\ \text{s}\text{.t}\text{.}{y}_i\left(W^{\text{T}}{x}_i+b\right)\ge \rho /2,i=1,2,\cdots ,n\end{array}$ (1)

于是，中间那条分类线相当于 $W^{\text{T}}{x}_i+b=0$ ；对于圆点的数据点有 $W^{\text{T}}{x}_i+b\le -\rho /2$，对于三角的数据点有 $W^{\text{T}}{x}_i+b\ge \rho /2$。

再根据支持向量数据点到分类线的距离，推导出关于“几何间隔”最大化的模型：

$\begin{array}{l}\max \rho /\Vert W\Vert \\ \text{s}\text{.t}\text{.}{y}_i\left(W^{\text{T}}{x}_i+b\right)\ge \rho /2,i=1,2,\cdots ,n\end{array}$ (2)

最后，经过重新量化，去掉ρ，得到最终的线性分类器模型如下：

$\begin{array}{l}\min \frac{1}{2}{W}^{\text{T}}W\\ \text{s}\text{.t}\text{.}{y}_i\left(W^{\text{T}}{x}_i+b\right)\ge 1,i=1,2,\cdots ,n\end{array}$ (3)

这里的约束条件，相当于，对于圆点的数据点有 $W^{\text{T}}{x}_i+b\le -1$，对于三角的数据点有 $W^{\text{T}}{x}_i+b\ge 1$。

模型(3)的求解过程是通过拉格朗日乘子法，为每一个训练数据点添加拉格朗日乘子 ${\alpha }_i\ge 0,i=1,2,\cdots ,n$，原问题转化为

$L_P\left(W,b,{\alpha }_i\right)=\underset{w,b}{\min }\underset{{\alpha }_i\ge 0}{\max }\left\{\frac{1}{2}{W}^{\text{T}}W-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i\left(y_i\left(W^{\text{T}}{x}_i+b\right)-1\right)}\right\},$

再通过 $L_P$ 对 $W,b$ 求偏导等于0，得到

$\frac{\partial L\left(W,b\right)}{\partial W}=0\Rightarrow W-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i{y}_i{X}_i}=0$ (4)

$\frac{\partial L\left(W,b\right)}{\partial b}=0\Rightarrow {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i{y}_i}=0$

于是，得到对偶问题

$\begin{array}{l}\max L_D\left(\alpha \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i-\frac{1}{2}{\displaystyle \underset{i,j}{\sum }{\alpha }_i{\alpha }_j{y}_i{y}_j{X}_i^{\text{T}}{X}_j}}\\ \text{s}\text{.t}\text{.}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i{y}_i}=0,{\alpha }_i\ge 0\end{array}$

然后，用SMO算法进行对偶问题求解，求出各个 ${\alpha }_i,i=1,2,\cdots ,n$，再带回(4)式，就得到W的值。这里求出来的 ${\alpha }_i$ 中大于0的就对应支持向量i。再由各个支持向量满足的表达式 ${\alpha }_i\left[y_i\left(W^{\text{T}}{X}_i+b\right)-1\right]=0$ 求出b、并进行平均得到最终的 $\hat{b}$，从而得到最终的分类线如下

$f\left(X\right)={\displaystyle \underset{i=1}{\overset{n_s}{\sum }}{\hat{\alpha }}_i{y}_i{X}_i^{\text{T}}\cdot X}+\hat{b}.$

2) SVM的软边界模型

实际生产和生活中，很多数据往往是线性不可分的，但，如果还想用线性分类器去分，又想尽量减少分类错误，那么可以像下图5那样，为每个数据点加上松弛变量 ${\xi }_i\ge 0$，使得，对于三角的数据点，由原来的 $W^{\text{T}}X+b\ge 1$ 松弛到 $W^{\text{T}}X+b\ge 1-{\xi }_i$ ；对于圆点的数据点，由原来的 $W^{\text{T}}X+b\le -1$ 松弛到 $W^{\text{T}}X+b\le -1+{\xi }_i$。

Figure 5. Soft margin classification problem

图5. 软边界分类问题

得到的相应“软边界”模型如下：

$\begin{array}{l}\min \Phi \left(W\right)=1/2W^{\text{T}}W+C{\displaystyle \sum {\xi }_i}\\ \text{s}\text{.t}\text{.}{y}_i\left(W^{\text{T}}{x}_i+b\right)\ge 1-{\xi }_i,{\xi }_i\ge 0,i=1,2,\cdots ,n\end{array}$

对于这个模型，把松弛变量 ${\xi }_i$ 加进目标函数里作为惩罚，惩罚的力度由参数C来决定。其求解过程和上面线性分类器模型的求解过程类似。

3) SVM中的核函数

通过函数映射 $\phi \left(X\right)$，把数据从低维空间映射到高维空间，使得低维空间里线性不可分的数据到了高维空间里变成线性可分，从而构造高维空间里的线性SVM分类器进行解决，如下图6。

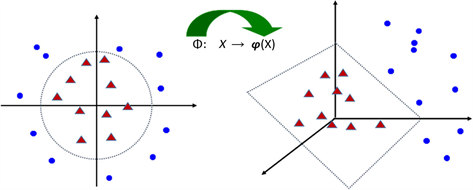
Figure 6. The mapping of linearly inseparable data in two-dimensional space to three-dimensional space to make it linearly separable

图6. 把二维空间线性不可分的数据映射到三维空间使其线性可分

但那样的映射，一般很难找，而在SVM的模型求解过程的对偶问题模型中以及求解的结果中，主要涉及到数据点的内积形式，比如下面两个式子中类似 $X_i^{\text{T}}X$ 形式，

$\max L_D\left(\lambda \right)={\displaystyle \underset{i=1}{\overset{Q}{\sum }}{\lambda }_i}-\frac{1}{2}{\displaystyle \underset{i=1}{\overset{Q}{\sum }}{\displaystyle \underset{j=1}{\overset{Q}{\sum }}{\lambda }_i{\lambda }_j{y}_i{y}_j\left(X_i^{\text{T}}{X}_j\right)}}$

$f\left(X\right)={\displaystyle \underset{i=1}{\overset{n_s}{\sum }}{\hat{\alpha }}_i{y}_i{X}_i^{\text{T}}\cdot X}+\hat{b}$

如果想象一下，数据点映射到高维空间，上面两个式子里也就对应 $\phi {\left(X_i\right)}^{\text{T}}\phi \left(X_j\right)$ 形式，于是研究者们想到去找这样的函数 $K\left(X_i,X_j\right)=\phi {\left(X_i\right)}^{\text{T}}\phi \left(X_j\right)$，即找K函数，这就是核函数，而不是去找 $\phi$。于是，在引入核函数以后，得到SVM的分类超平面为：

$f\left(X\right)={\displaystyle \underset{i=1}{\overset{n_s}{\sum }}{\hat{\alpha }}_i{y}_{i}K\left(X_i^{\text{T}}\cdot X\right)}+\hat{b}$

对于新来的测试样本X，可以带入上式，算出其决策函数值 $f\left(X\right)$，从而决定其类属。这样的K函数在一般的软件里通常有：

线性核函数： $K\left(X_i,X_j\right)={X^{\prime }}_i\ast X_j$ ；

多项式核函数： $K\left(X_i,X_j\right)={\left(\sigma \ast {X^{\prime }}_i\ast X_j+b\right)}^p$ ；

径向基核函数(或者叫高斯核函数)： $K\left(X_i,X_j\right)=\exp \left(-\frac{{\Vert X_i-X_j\Vert }^2}{2{\sigma }^2}\right)$ ；

sigmoid核函数： $K\left(X_i,X_j\right)=\tanh \left(\sigma \ast {X^{\prime }}_i\ast X_j+b\right)$。

2. 理论教学中的几个关键细节理解

在上面描述的支持向量机理论过程中，有很多关键细节，在教学过程中，理解起来非常有难度，我们给出详细的解释。

理解1：“函数间隔”与“几何间隔”，以及SVM最大化的Margin究竟是什么？

解释：将图4进一步细化，把其中的直线方程补充上，如下图7。

Figure 7. Three lines and margin in binary classification problem

图7. 二分类中三条直线及Margin等情况

在上面线性分类器模型的推导过程中，图7中的z2和z3线就分别是两类样本点的边界，最大化两类样本的分类边界间的间隔，这个间隔，比较难理解，模型的推导过程，目标函数是怎么从最大化ρ，

到了最大化 $\frac{1}{2}{W}^{\text{T}}W$ 的？

事实上，z2和z3线之间的“函数间隔”就是这两条平行线的表达式做差的绝对值，就是ρ，所以得到式(1)的模型；而它们之间的“几何间隔”就是其中一条线上的点到另一条线的距离，比如z2上的点 $X=\left(x_1,x_2\right)$，首先满足方程 $w_1\cdot x_1+w_2\cdot x_2+b=-\rho /2$，然后到z3 ( $w_1\cdot x_1+w_2\cdot x_2+b-\rho /2=0$ )距离为

$r=\frac{\left|w_1\cdot x_1+w_2\cdot x_2+b-\rho /2\right|}{\sqrt{w_1^2+w_2^2}}=\frac{\left|-\rho /2-\rho /2\right|}{\sqrt{w_1^2+w_2^2}}=\frac{\rho }{\sqrt{w_1^2+w_2^2}}=\frac{\rho }{\Vert W\Vert },$

所以，得到式(2)的模型。这样，最大化的“Margin”从代数上讲是ρ，从几何上讲是 $\frac{\rho }{\Vert W\Vert }$。那么，最大化哪一个更好呢？

实际上，要讲“几何间隔”最大，而不讲“函数间隔”最大。因为同一条直线的方程，将其各个项都乘以同一个倍数，它还是这条直线，但两条平行直线之间的“函数间隔”就变了，因为各自的常数项被乘以了倍数，做的差也比原来多了个倍数！比如，z2和z3线都变成：

$\begin{array}{l}z2:2w_1\cdot x_1+2w_2\cdot x_2+2b+\rho =0\\ z3:2w_1\cdot x_1+2w_2\cdot x_2+2b-\rho =0\end{array}$

那么，“函数间隔”就变成2ρ。而“几何间隔” $\frac{\rho }{\Vert W\Vert }$ 没变，因为求距离式子的分子分母都增大了同一个倍数，

$r=\frac{\left|2w_1\cdot x_1+2w_2\cdot x_2+2b-\rho \right|}{\sqrt{{\left(2w_1\right)}^2+{\left(2w_2\right)}^2}}=\frac{\left|-\rho -\rho \right|}{\sqrt{{\left(2w_1\right)}^2+{\left(2w_2\right)}^2}}=\frac{2\rho }{\sqrt{{\left(2w_1\right)}^2+{\left(2w_2\right)}^2}}=\frac{\rho }{\Vert W\Vert }$

所以要讲“几何间隔” $\frac{\rho }{\Vert W\Vert }$ 最大。当然，在下面一条理解里，当把图7中的三条直线一起重新量化后，发现要最大化的Margin实际上是量化后的 $\frac{2}{\Vert W\Vert }$。解释完毕！

理解2：线性分类器模型中的目标函数如何由 $\frac{\rho }{\Vert W\Vert }$ 变成 $\frac{1}{2}{W}^{\text{T}}W$ 的？约束条件又如何从 $y_i\left(W^{\text{T}}{x}_i+b\right)\ge \rho /2$ 变成 $y_i\left(W^{\text{T}}{x}_i+b\right)\ge 1$ 的？

解释：如果把图7中的三条直线的方程分别都除以ρ/2，以改变比例、重新量化，得到

$\begin{array}{l}z3:w_1/\left(\rho /2\right)\cdot x_1+w_2/\left(\rho /2\right)\cdot x_2+b/\left(\rho /2\right)=1\\ z1:w_1/\left(\rho /2\right)\cdot x_1+w_2/\left(\rho /2\right)\cdot x_2+b/\left(\rho /2\right)=0\\ z2:w_1/\left(\rho /2\right)\cdot x_1+w_2/\left(\rho /2\right)\cdot x_2+b/\left(\rho /2\right)=-1\end{array}$

或者，写成

$\begin{array}{l}z3:{\bar{w}}_1\cdot x_1+{\bar{w}}_2\cdot x_2+\bar{b}=1\\ z1:{\bar{w}}_1\cdot x_1+{\bar{w}}_2\cdot x_2+\bar{b}=0\\ z2:{\bar{w}}_1\cdot x_1+{\bar{w}}_2\cdot x_2+\bar{b}=-1\end{array}$

或者，再写成

$\begin{array}{l}z3:w_1\cdot x_1+w_2\cdot x_2+b=1\\ z1:w_1\cdot x_1+w_2\cdot x_2+b=0\\ z2:w_1\cdot x_1+w_2\cdot x_2+b=-1\end{array}$ (5)

则，一个支持向量到分类线的距离就变成 $r=\frac{1}{\Vert W\Vert }$，那么分类线两侧的距离之和，也就是z2和z3线之间的距离就是 $\frac{2}{\Vert W\Vert }$，于是，应该追求 $\frac{2}{\Vert W\Vert }$ 的最大化，即这就是支持向量机最终要最大化的Margin。同时，为了求解的方便，也相当于追求 $\frac{1}{2}{\Vert W\Vert }^2$ 的最小化，或者追求 $\frac{1}{2}{W}^{\text{T}}W$ 的最小化。

另外，根据(5)式，z2和z3线两边的数据点必须满足约束条件 $y_i\left(W^{\text{T}}{X}_i+b\right)\ge 1$。于是，最终的线性分类器模型就是：

$\begin{array}{l}\min \frac{1}{2}{W}^{\text{T}}W\\ \text{s}\text{.t}\text{.}{y}_i\left(W^{\text{T}}{X}_i+b\right)\ge 1,i=1,2,\cdots ,n.\end{array}$

解释完毕！

理解3：把线性分类器模型转换成对偶问题求解以后，得到的 $\hat{\alpha }={\left({\hat{\alpha }}_1,\cdots ,{\hat{\alpha }}_n\right)}^{\text{T}}$，为什么其中 ${\hat{\alpha }}_i>0$ 对应的样本i就是支持向量 [11] ？

解释：在下面式子中

$L_P\left(W,b,{\alpha }_i\right)=\underset{w,b}{\min }\underset{{\alpha }_i\ge 0}{\max }\left\{\frac{1}{2}{W}^{\text{T}}W-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i\left(y_i\left(W^{\text{T}}{X}_i+b\right)-1\right)}\right\},$

关于 ${\alpha }_i$ 求最大时(把W和b当常数看)，得到

$\underset{{\alpha }_i\ge 0}{\max }{L}_P\left(W,b,\alpha \right)=\underset{{\alpha }_i\ge 0}{\max }\frac{1}{2}{W}^{\text{T}}W-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i\left(y_i\left(W^{\text{T}}{X}_i+b\right)-1\right)},$ (6)

如果 $X_i$ 是支持向量，那么就有 $y_i\left(W^{\text{T}}{X}_i+b\right)-1=0$，即 $y_i\left(W^{\text{T}}{X}_i+b\right)=1$，则(6)式的最大化就只由 $\frac{1}{2}{W}^{\text{T}}W$ 决定，而 ${\alpha }_i$ 取任何值都对目标函数的最大化没有影响，其中就可以取大于0的值；而对于非支持向量，则有 $y_i\left(W^{\text{T}}{X}_i+b\right)-1>0$，即 $y_i\left(W^{\text{T}}{X}_i+b\right)>1$，而 ${\alpha }_i\ge 0$，则有 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i\left(y_i\left(W^{\text{T}}{X}_i+b\right)-1\right)}\ge 0$，为了满足最大化的要求，必须 ${\alpha }_i=0$，才能使得 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i\left(y_i\left(W^{\text{T}}{X}_i+b\right)-1\right)}=0$，从而使得(3)式最大化。这样一来，只有对应支持向量的 ${\alpha }_i$ 有可能大于0，而非支持向量对应的 ${\alpha }_i$ 一定等于0；当然， ${\alpha }_i$ 等于0的不一定是非支持向量。综上， ${\alpha }_i>0$ 对应的数据点 $X_i$ 就一定是支持向量。解释完毕！

理解4：对于同一个训练集，得到的分类超平面，唯一吗？

解释：分类超平面，在二维平面里，就是分类直线。从下面图8中的三个图来看，图(1)中实线是分类线，在保持两条虚线之间距离不变的同时(即保持Margin不变)，三条线一起做适当的旋转，得到图(2)中的三条粗一点的线，此时，图(1)中的支持向量和图(2)中的支持向量稍微有些变化。旋转以后形成的支

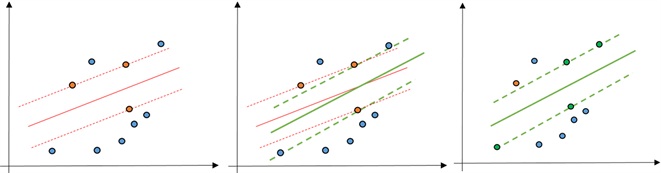
Figure 8. Non-unique case of support vector machine classification line

图8. 支持向量机分类直线的不唯一情况

持向量机分类情况如图(3)。由此可以看出，从理论上讲，对于同一个训练集，得到分类直线可以不唯一，或者得到的分类超平面可以不唯一，但从实验出发，很多数据点都只能算出来一个分类超平面，而不是恰好能有两个分类超平面的情况，实验方面还需要恰好能产生这样的数据点来进行实践。

解释完毕！

3. Matlab、R语言和Python在Iris数据上的实验

下面给出三个软件上的实验代码及得到的实验结果中如何获取支持向量机模型。

1) Matlab实验代码

我们的实验，使用了台湾林志仁教授他们开发Matlab工具包libsvm [12]。这个包，需要按照一定的流程在matlab里进行安装，才可以使用。

① 代码

② 实验中得到的SVM模型的获取

当model这个变量生成以后，可以在matlab命令窗口执行它，得到下面结果

要获得最后的分类超平面 $f\left(X\right)={\displaystyle \underset{i=1}{\overset{n_s}{\sum }}{\hat{\lambda }}_i{y}_{i}K\left(X_i^{\text{T}}\cdot X\right)}+\hat{b}$，需要针对每个支持向量i获得核函数前面的

系数 ${\hat{\lambda }}_i{y}_i$，以及分类面的截距 $\hat{b}$。这个实验，分三类，构造了三个分类超平面，即第一类和第二类之间的一个分类面，第一类和第三类之间一个分类面，第二类和第三类之间一个分类面，可以分别记为1/2，1/3，2/3的三个分类面。那么需要找到每个分类面涉及到的系数和截距。

首先，截距的获得比较简单，在Matlab命令窗口执行model.rho，就得到三个数：0.0745、0.2416、0.0592，这就是那三分类面截距的相反数。

其次，在命令窗口执行model.sv_coef就可以得到36 × 2的向量，这是那36个支持向量中每个支持向量对应的两个系数，为什么是两个系数呢？因为我们的分类面是1/2，1/3和2/3，那么第一类的样本就有可能在1/2分类面里是支持向量，也有可能在1/3里是支持向量；第二类的样本有可能在1/2中是支持向量，也有可能在2/3中是支持向量；同理，第三类的样本有可能在1/3里是支持向量，也有可能在2/3里是支持向量，且这些系数值的正负情况，就表明它们在一个分类面的相应正负类里当作支持向量的。具体地，我们取出第2、3号样本支持向量对应的系数、以及第41、90号样本对应的系数出来稍做分析，它们的系数值见下面的表1，为了节省空间，其他支持向量的系数就不再列入表格。

2号样本的两个系数的值都是2，都非零，且2号样本本身是第一类的，说明它在1/2和1/3中都当了支持向量，并且这两个系数值就相当于它在下面分类面中的 ${\hat{\lambda }}_2{y}_2$ 的值；

3号样本的两个系数值分别是0.2580和0，后面一个系数值是0，且3号样本本身是第一类的，说明它只在1/2分类面中当了支持向量，而在1/3中不是支持向量，且在1/2中的作用相当于1/2分类面上面方程中的 ${\hat{\lambda }}_3{y}_3$ 的值；

41号样本的两个系数的值是−0.2144和2，都非零，根据上面第④项中关于sv_indices的分析来看，该样本本身属于第二类，那么它有在1/2和2/3这两个分类面中都当了支持向量，第一个系数是−0.2144，说明它在1/2中当了支持向量，且这个系数值是负数，说明它在1/2分类面的负类中当了支持向量；第二个系数值2，说明它在2/3中当了支持向量，且是正类的支持向量；

90号样本，是训练集中的最后一个样本，且它本身是第三类的，其两个结果系数是−0.4835和0，说明它在1/3当了支持向量，而在2/3中没有当支持向量，且因为它的值为负的，更说明了该样本在1/3这个分类面的负类中当作了支持向量的，这个非零系数值就是它在分类面1/3中的 ${\hat{\lambda }}_{90}{y}_{90}$。

实际上，根据SVM的原理、实验所选取的核函数和model.sv_coef中的数据，就可以把三个分类面依次写出来。由于这里数据太多，就不再一一分析和整理，留给读者去实验和把三个模型写出来。

Table 1. The coefficients of support vector in the classification plane

表1. 支持向量在分类面中的系数结果

2) 基于R语言的实验

R语言里，使用了e1071包，它提供了对libsvm的接口。

① 代码

② 实验中得到的SVM模型的获取

在Rstudio命令窗口(Console)，输入svmfit$就可以看到如下提示

在提示里，我们就可以选择所提示的各个项并回车，去查看一些实验参数及结果。

接下来，如果在上面图里的界面里$后面选择rho，即在Console窗口执行了svmfit$rho，就得到三个分类面的截距；同理，执行了svmfit$coefs，就能得到各个分类面的系数；这二者都和上面Matlab实验里的解释类似，这里不再多说。

3) 基于python的实验代码

Python实验里使用了其中的sklearn中的svm包，sklearn.svm模块提供了很多模型供我们使用，本文使用的是svm.SVC，它是基于libsvm实现的。.

① 代码

② 实验中得到的SVM模型的获取

在Python的Console窗口写classifier.，然后按Tab键，就可以得到下图所示的下拉选项，在选项里选择某项，并回车，就得到了相应的实验结果参数

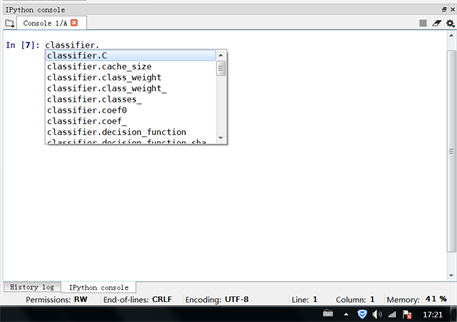
同样的，可以在上面窗口里进行选择，找到三个分类面的系数和截距。

4. 总结

本文将SVM分类的理论知识的主体结构进行了概述，将SVM模型本身及其推导过程中的某些细节的理解进行了精细的解释；最后还给出了目前大家常用的三个软件上的实验，即Matlab、R语言和Python在iris数据上的实验，还给出了寻找各个实验中所用到的相应支持向量机模型的方法。这些工作，从不同的角度、不同的计算机语言针对支持向量机的分类进行了理解和分析，这对于SVM的学习和使用提供了重要的参考，使得支持向量机的教学过程得到了进一步的提升。