多因素下鱼类迁徙预测模型

Prediction Model of Fish Migration under Multiple Factors

摘要: 每一种生物都对自身的生存环境存在一定的要求，全球海洋温度的升高使得一些海洋生物离开原来生活的地方，去寻找更适宜生存的栖息地。海洋生物的这一迁徙现象给依赖这一资源生存的渔业公司造成很大困扰。鲱鱼和鲭鱼为苏格兰经济作出重要贡献，对当地渔业公司至关重要，随着近年来海水温度不断上升，这两种鱼类也将往北逐渐进行迁徙。为了让苏格兰当地小型渔业公司对这一迁徙现象及早做出有效应对措施，我们通过收集近几年这两种鱼的数量以及当地海水温度数据建立模型，对两类鱼迁徙位置进行了预测。同时通过引入海温变化速率这一参数，我们研究了鱼类迁徙速度与海水温度上升速度之间的关系。利用上述模型，我们可以掌握鱼群未来分布位置以及海水温度变化快慢对鱼群迁徙速率的影响，为小型渔业公司制定有效应对策略提供依据。

Abstract: Every living creature has certain requirements for its own living environment. The global warming of ocean temperature makes some Marine creatures leave their original living place to find a more suitable habitat. This migration of Marine life is causing problems for fishing companies that depend on the resource. Herring and mackerel are important to the Scottish economy and vital to local fishing companies, and are due to migrate north as sea temperatures have risen in recent years. In order to enable small local fishing companies in Scotland to respond effectively and early to this migration phenomenon, the migration location of the two species of fish was predicted by collecting data on their populations and local sea temperature in recent years. At the same time, by introducing the parameter of SST change rate, we studied the relationship between fish migration rate and seawater temperature rise rate. Using the above model, we can grasp the future distribution location of fish stocks and the impact of sea temperature change on the migration rate of fish stocks, so as to provide a basis for small fishery companies to formulate effective coping strategies.

1. 引言

在全球海水温度逐渐升高的背景下，我们需要对苏格兰附近的鲱鱼和鲭鱼未来的分布位置进行预测。由于生物的迁徙受众多环境因素影响，我们针对其中影响力最大的营养级、水质、水流、水温四个主要影响因子进行建模。我们构建栖息地适度子模型来研究海表温度(温度数据来自BOA网络服务器)以及海表温度梯度对鲱鱼和鲭鱼这两种鱼类生存的影响，评价它们对某一生存环境的适应程度，构建海洋生态系统营养动力变化子模型研究营养级(食物)对两类鱼生存的影响，构建二维海水动力水质子模型研究海水流速、作用力等对鱼类生存、迁徙的影响，最后我们对搜集到的当地近几年海水温度变化数据进行处理，从而得到在原栖息地环境下这四大因素受其他环境因素影响的影响因素子模型。同时借此机会我们对两类鱼的各项生存适宜指数有一定了解，这有助于对鲱鱼和鲭鱼的迁徙位置进行判定。得到这四个影响因素子模型之后，我们将栖息地适度因子、营养级、水动力与海水温度这四大因素子模型的输出结果进行标准化处理，消除数据量级影响之后作为输入层，将鱼群未来经纬度作为输出层，利用神经网络模型对鱼群未来所处位置进行预测，得到在一般情况下两类鱼未来的经纬度位置。

当海面温度上升越快，SH值下降速度越快，营养级改变越迅速，鱼群改变栖息地的速度越快，因此海水温度变化的速率对鱼群的迁徙速度密切相关。我们在预测模型基础上引入海水升温速率参数，通过改变这一参数的大小就可以研究海水升温速度对当地鱼类资源迁徙速率的影响。

2. 基本假设

假设水温变化足以导致鲭鱼与鲱鱼种群移动，未移动的鱼数量极少，不影响模型建立。

假设营养级、水质、水流、水温四个影响因子相互独立，彼此之间的关联忽略不计。

假设鱼群的生态活动正常，不收特殊地质灾害的影响。

假设研究时无重大事故导致渔获量激增。

3. 影响因素子模型

3.1. 栖息地适度子模型

我们借助栖息地模型来研究海表温度以及海表温度梯度对鲱鱼和鲭鱼这两种鱼类生存的影响。为了方便，我们将各区海域内两类鱼的捕获量(从苏格兰及北海渔场附近其他国家渔业杂志中得到)看作该区海域内的此类鱼的数量。见图1我们将某一海域分为许多小海区，设立海表温度探测点计算SST_i,j点处的水平梯度GSST_i,j，并得到公式如下：

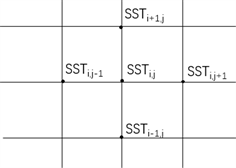
Figure 1. Schematic diagram of fishing ground

图1. 渔场示意图

$GSS{T}_i=\sqrt{\frac{{\left(SS{T}_{i+1,j}-SS{T}_{i-1,j}\right)}^2+{\left(SS{T}_{i,j+1}-SS{T}_{i,j-1}\right)}^2}{2}}$

NET_i,j为(i,j)海区内年鱼类数量，NET_max为该海域渔获数量的最大值。我们设捕获鱼类数量最多的海区为该类鱼资源分布最多的海区，将其适应性指数定为1。借助以上两个参数表示(i,j)海区内鱼类的适应性指数：

$S{I}_i=\frac{NE{T}_i}{NE{T}_{\max }}$

由于各海区海表温度已知，我们建立水平梯度GSST_i,j、适应性指数定SI_i与海表温度SST_i,j之间的关系：

$S{I}_{GSST}={\text{e}}^{0.0035x\left(x-10.8351\right)}$ (1)

$S{I}_{SST}=0.6306+451.91{\text{e}}^{-x}$ (2)

$S{I}_{GSST}={\text{e}}^{0.0875x\left(x-3.5802\right)}$ (3)

$S{I}_{SST}=0.358+4.3{\text{e}}^{-x}$ (4)

式(1)、(2)为鲱鱼，式(3)、(4)为鲭鱼。我们采用算式平均法将相关影响因素代入公式计算HSI：

$HSI=\sqrt{S{I}_{GSST}S{I}_{SST}}$

对生物栖息地进行判断时，我们一般认为当HSI大于0.6，就可以认为此地适宜该物种生存。将海区水温10.545℃、2.1491℃代入，我们得到该海区鲱鱼的HSI为0.7973，鲭鱼的HSI为0.8103，均大于0.6，接近1，因此计算结果与实际相接近，模型具有可靠性。

3.2. 海洋生态系统营养动力变化子模型

我们基于东北大西洋主要渔获种类营养级数据 [1] 建立营养变化模型，大西洋鲱鱼与鲭鱼属于中高级食肉动物，引入营养级平衡指标FIB，借此指出北海渔场渔业与生态环境是否处于总平衡状态。FIB计算公式如下：

$FIB=\text{log}\left(T_i*s^{-n_i}\right)-\log \left(T_0*s^{-n_0}\right)$ [1]

s为营养转化效率设为0.1。n_i表示i年的平均营养级，T_i是第i年的渔获量若FIB小于零，说明当前捕捞量高于理论捕捞量，生态平衡遭到破坏，长此以往物种将灭绝。我们将1995~2015年的鲭鱼与鲱鱼渔获量数据代入计算，取1990年的平均营养级n₀和渔获量T₀作为参考值。将数据导入公式后我们绘制结果趋势图，见图2：

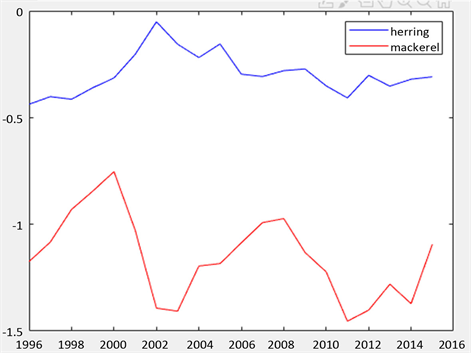
Figure 2. The nutrient level equilibrium index of mackerel and herring

图2. 鲭鱼、鲱鱼的营养级平衡指数

数据显示，二者的FIB值都小于零，而且鲭鱼的FIB值大多数小于1。说明当地渔区当地的捕捞产量过度，捕捞产量的增加不足以弥补平均营养级的降低，海洋生态结构系统的平衡遭到破坏。同时，鲱鱼的所有FIB指数都比鲭鱼高，说明两种情况：首先是捕捞技术在不断更进，鲭鱼被捕数量增加。再者便是鲱鱼数量相对减少，整体捕捞数量便有所减缓。在这样的条件下，鱼群会选择迁徙至其他地方以逃避过度捕捞带来的灭顶之灾。

3.3. 二维海水动力水质子模型

根据问题背景，我们将原始水动力方程组 [2] 修改成如下方程组：

$\begin{array}{c}\frac{\partial h\bar{u}}{\partial t}+\frac{\partial h{\bar{v}}^2}{\partial x}+\frac{\partial h\bar{v}\bar{u}}{\partial y}=-\theta \bar{u}h-gh\frac{\partial \eta }{\partial y}-\frac{h}{{\rho }^{\prime }}\frac{\partial Pa}{\partial y}-\frac{g{h}^2}{2{\rho }^{\prime }}\frac{\partial \rho }{\partial y}+\frac{{\tau }_{sx}}{{\rho }^{\prime }}-\frac{{\tau }_{bx}}{{\rho }^{\prime }}\\ -\frac{1}{\rho }\left(\frac{\partial m_{yx}}{\partial y}+\frac{\partial m_{yy}}{\partial x}\right)+\frac{\partial \left(h{F}_{xx}\right)}{\partial x}+\frac{\partial \left(h{F}_{yy}\right)}{\partial y}+h{v}_{s}S\end{array}$

$\begin{array}{c}\frac{\partial h\bar{u}}{\partial t}+\frac{\partial h{\bar{u}}^2}{\partial x}+\frac{\partial h\bar{v}\bar{u}}{\partial y}=\theta \bar{v}h-gh\frac{\partial \eta }{\partial x}-\frac{h}{{\rho }^{\prime }}\frac{\partial Pa}{\partial x}-\frac{g{h}^2}{2{\rho }^{\prime }}\frac{\partial \rho }{\partial x}+\frac{{\tau }_{sx}}{{\rho }^{\prime }}-\frac{{\tau }_{bx}}{{\rho }^{\prime }}\\ -\frac{1}{\rho }\left(\frac{\partial m_{xx}}{\partial x}+\frac{\partial m_{xy}}{\partial x}\right)+\frac{\partial \left(h{F}_{xx}\right)}{\partial x}+\frac{\partial \left(h{F}_{xy}\right)}{\partial x}+h{u}_{s}S\end{array}$

其中t为时间，x和y是直角坐标系，u，v为海洋表面流速V在x和y方向上的分量，海洋表面流速V为7.8 km/h。P为苏格兰沿海海面大气压，取101.32 kPa。 $\rho$ 为大西洋海水密度，此处取1.04 × 10³ kg/m³。 ${\rho }^{\prime }$ 取标准水密度1.0 × 10³ kg/m³。 $\theta$ 的含义是Corolis力参数，与地球自转角速率 $\omega$ 和苏格兰地理纬度 $\gamma$ 有如下关系：

$\theta =2\omega \sin \gamma$

而m_xx，m_xy，m_yx和m_yy为辐射映射分力，F_xx，F_xy，F_yx和F_yy为水平粘滞应力项。S为广义源汇项，由方程标准化后的流向剩余项、扩散项剩余项以及坐标系下的源项 [3] 三部分组成。底部应力遵循二次摩擦定律，可给出公式如下：

$\frac{\overline{{\tau }_b}}{{\rho }^{\prime }}=\mu \overline{v_b}\left|\overline{v_b}\right|\frac{\overline{{\tau }_b}}{{\rho }^{\prime }}=\mu \overline{v_b}\left|\overline{v_b}\right|$

其中，

$\overline{{\tau }_b}=\left({\tau }_{bx},{\tau }_{by}\right)$

$\mu$ 为阻力系数，而曼宁公式是明渠道流量或速度经验公式与底床糙率长度 [4]，将其与 $\mu$ 结合我们可以得出

$\{\begin{array}{l}\mu =\frac{g}{{\left(M{h}^{\frac{1}{6}}\right)}^2}\\ M=\frac{25.4}{k_s^{\frac{1}{6}}}\end{array}$

k是转换常数，国际单位制中值为1； [4] $\overline{u_b}=\left(u_{bx},u_{by}\right)$ 是海水底部水流速度为8.3 km/h。代入水动力方程组计算，结果见图3：

Figure 3. Annual catch

图3. 一年捕获量

我们可知，该地流量在11~12月有一个小高峰，在7~9月出现另一个高峰，通过查询发现，鲭鱼为远洋洄游性鱼类，夏季结群游向近海生殖，苏格兰在8月多次作业捕捞 [4]。而鲱鱼于1~3月洄游至北海，又是一个捕捞高峰。通过2016~2017实际数据相比较，我们发现两者有略微偏移，说明我们模拟的效果良好。

3.4. 海水温度的利用与分析

根据BOA网络服务器提供的2004~2019年的海水温度数据，筛选处理得到56.6度N6.5度E且距离海平面5dbar的海平面温度T℃，并计算第i年与第I − 1年的温度变化差 $\Delta T$，我们将这组数据放置于后面统一分析(详见4.2)。

4. 综合因素下的神经网络预测模型

4.1. 神经网络预测模型基础构建

对于第i个影响因子x_i，将代表因子的原始数据标准化并归一化到区间[0,1]，即

${x^{\prime }}_i=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }}$ [5]

${x^{\prime }}_i$ 为第i个影响因子归一化后数据，x_min，x_max为第i个影响因子原始数据的最大值与最小值。 $X_p={\left({x^{\prime }}_1,{x^{\prime }}_2,\cdots ,{x^{\prime }}_m\right)}^{\text{T}}\left(1\le p\le m\right)$ 为输入， $Y_p={\left({y^{\prime }}_1,{y^{\prime }}_2,\cdots ,{y^{\prime }}_m\right)}^{\text{T}}\left(1\le p\le m\right)$ 为输出， $\left(X_p,Y_p\right)$ 为输入样本集的第p个样本。要说明的是，W_ij表示前层第i个节点到本层第j个节点的连接权值 [6]，第p个样本输出层误差均方差为

$E_p=\frac{1}{2}{\displaystyle \underset{j}{\overset{n}{\sum }}{\left(y_j^{\left(p\right)}-f{l}_j^{\left(p\right)}\right)}^2}$

而对于 $x_i\in \left(0,1\right)$ 为隐含—输出层，y_i为输出-隐含层，t为动量系数则有：

$\begin{array}{l}{\omega }_{ij}\left(\iota +1\right)={\omega }_{ij}\left(t\right)-x_i\left(\frac{\partial E_p}{\partial {\omega }_{ij}}\right)+\eta \left[{\omega }_{ij}\left(\iota \right)\right]\\ {\omega }_{ij}\left(\iota +1\right)={\omega }_{ij}\left(t\right)-y_i\left(\frac{\partial E_p}{\partial {\omega }_{ij}}\right)+\eta \left[{\omega }_{ij}\left(\iota \right)\right]\end{array}$

4.2. 神经网络下的温差预测

将过去的温差数据 $\Delta T$ 作为该模型的二级指标，未来50年的温差作为一级指标，仿真模拟得到未来50年的预测温差，同时可得51组距离海平面5 dbar的海平面温度T值，我们将其余原有的数值整理，见表1：

Table 1. Temperature forecast for 2004-2069

表1. 2004~2069年温度预测

从表1可以看出，温度最低值2.6011℃为已知过去海水温度，最高值7.4169℃为我们的预测温度。通过对比我们发现，海平面5 dbar的海平面温度T虽然上升速度较为缓慢，但是如果不加以控制，必然会破坏生物系统，给当地经济带来重创。我们将这组温度预测数据作为海水温度指标因子，用来预测鱼群位置。

4.3. 鱼群位置分析

Table 2. Secondary index factor table

表2. 二级指标因子表

我们将一二级指标分配表进行总结，见表2，同时建立预测模型预测鱼群位置，设定大西洋鲱鱼最佳适应水温为9.7℃~12.2℃，鲭鱼最佳适应水温为1.6℃~2.7℃。得到50年后鲱鱼鱼群最可能位于4.278˚E ± 0.2˚，60.948˚N ± 0.2˚，鲭鱼鱼群最可能位于3.523˚E ± 0.2˚，59.575˚N ± 0.2˚，我们将迁徙路线在地图上做简要标记，见图4：

Figure 4. Migration route

图4. 迁徙路线图

目前大西洋鲭鱼种群所处范围在1.792˚W，60.024˚N (方块所示)，鲭鱼最可能出现的位置向东移动6.07˚，合约3673.7 km，向北移动0.924˚，合约51.282 km，而鲱鱼种群所处范围在2.768˚W，59.394˚N (三角所示)，鲱鱼最可能出现的位置向东移动6.291˚，合约698.301 km，向北移动0.181˚，合约10.0445 km。

5. 改变海水温度因子后的鱼群迁徙预测模型改进

5.1. 参数进一步的改进与确定

海面温度上升越快，SH值下降速度越快，营养级改变越迅速，鱼群迁徙速度越快，导致公司的捕捞量T_i减少越快。因此公司在不做出改变情况下，能够运营的年限长由海水升温速率决定。根据分析，我们计算出2004~2019年海面温度逐年上升速率v_h，取v_h的最小正值，即每月上升0.12℃为最佳情况下海温的上升速率。当v_h取到最大值即每月上升3.84℃为最坏可运营情况 [7]。而最初的未来50年海温变化根据一般状态得到为大概率情况。

5.2. 海水升温速率影响下的结果分析

取不同海水温度变化速度值，重新使用神经网络预测模型计算，输入层变为已知捕捞量T_i，隐含层神经元个数不变，输出层为未来捕捞量 ${T^{\prime }}_i$，训练次数为1000，将三种情况下所得数据绘制于统一图中，见图5：

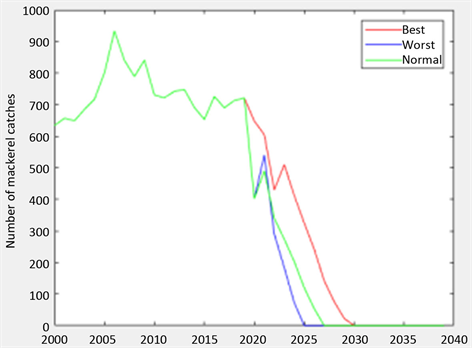
Figure 5. Herring caught over the next 50 years

图5. 鲱鱼的未来五十年捕获情况

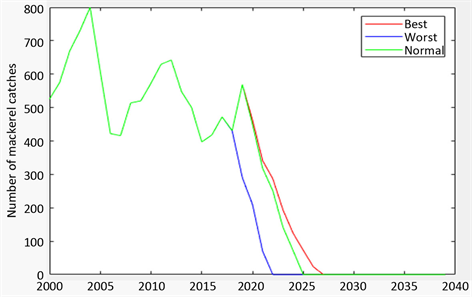
Figure 6. Mackerel caught in the next 50 years

图6. 鲭鱼的未来五十年捕获

图5为大西洋鲱鱼未来50年的捕获情况。其中蓝色的线代表最坏状态下公司捕捞量T_i随时间的数值变化情况，红色的曲线代表最坏状态，绿色的线代表最可能状态下T_i的值。通过图片我们发现，如果任由温度继续上升，该捕捞量最大可在继续供应十年，即小渔业公司在题设条件的最佳情况下可再捕捞10年，绿色的曲线位于红蓝两线之间，与x轴交点时间为2027年，则可得公司最可能继续捕捞7年。蓝色曲线与x轴交点的横坐标值最小，2025年T_i的值变为零，公司在该状态下捕捞量最多只能维持五年。图6为鲭鱼的未来五十年捕获情况。

通过图片我们发现，鲭鱼的整体捕获量虽然少于鲱鱼，但是由于鲭鱼处于更高层次的营养级，种群繁衍速度较鲱鱼来说更加缓慢，在原有T_i状态下，公司最快于2022年，即两年以后再无鲭鱼可捕获。但如果情况乐观，公司捕获时间相对延长，7年后(2027年)无法捕捞。而根据我们之前已模拟出的最可能的海面温度计算得到2025年是最可能公司无法捕获鲭鱼的重要时间点，综合来看，鲭鱼的捕获情况比鲱鱼要严重很多。

6. 结束语

本模型构建基于神经网络下的预测模型，解决了预测鱼群迁徙位置、研究海面温度变化速率对鱼群迁徙速率影响等实际问题，可以用于其他多重不确定因素多属性的预测问题与决策问题中，对海洋鱼类轨迹研究和社会经济效益评价方面有重大参考依据。

致谢

感谢互联网提供我们研究数据支持和指导老师的殷切指导。