1. 引言
张量是矩阵的高阶推广,广泛出现在图像处理、自动控制、医疗成像、超图论、高阶统计、弹性材料研究和数据分析等学科和工程中。近年来,很多专家和学者都对其进行了广泛探讨 [1] - [17]。本文在文 [13] 的基础上,继续讨论
-张量的判定问题,得到了一些新的判定条件。同时,利用新得到的
-张量的判定条件,给出了偶数阶实对称张量,即偶次齐次多项式正定性的判定方法。最后,给出了一些数值算例来说明新结果的有效性。
2. 预备知识
记
为复(实)数域,
。一个复(实)m阶n维张量
由
个复(实)元素构成 [1] [2] [3] [4] [5],其中
显然,2阶张量即为矩阵。此外,张量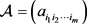 被称为对称的 [6] [7],若
被称为对称的 [6] [7],若
其中
为m个指标的置换群。若
,那么称张量
为非负张量。
定义2.1 [8]:张量 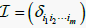 被称作单位张量,其中
被称作单位张量,其中
定义2.2 [6]:给定一个m阶n维张量
,若存在一个复数
和一个非零复向量
,满足
那么称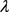 为张量
的特征值,x为张量
的关于特征值
的特征向量,其中
和
的第i个分量分别为
为张量
的特征值,x为张量
的关于特征值
的特征向量,其中
和
的第i个分量分别为
记m阶n次齐次多项式
为
(1)
其中
。当m为偶数时,
是正定的,若
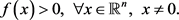
式(1)中的齐次多项式
可以表示为m阶n维对称张量
与
的乘积 [9],如下
(2)
当
是正定时,对称张量
也是正定的。
定义2.3 [10]:设
为m阶n维张量,如果对任意的
,
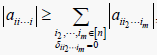 (3)
(3)
则称
是对角占优张量。若对于任意的
,
(4)
则称
是严格对角占优张量。
定义2.4 [11]:m阶n维张量
与矩阵
的乘积可表示为:
假设
表示
的任意非空子集,令
给定一个m阶n维张量
,令
引理2.1 [12]:若
为严格对角占优张量,则
为
-张量。
引理2.2 [13]:设
为m阶n维张量。若
是不可约的,
且至少有一个i使得严格不等式成立,则
为
-张量。
引理2.3 [13]:设
为m阶n维张量。如果存在一个正对角矩阵X,使得 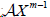 是
-张量,则
为
-张量。
是
-张量,则
为
-张量。
引理2.4 [14]:设
为m阶n维张量。若
(i)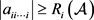 ,
,
,
,
(ii)
,
(iii)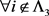 ,从i到j存在一个非零元素链使得
,
,从i到j存在一个非零元素链使得
,
则
为
-张量。
3. 主要结果
为了叙述方便,引入以下符号:对
,记
再记
易知 0 ≤ r < 1 ,且对任意的
,
从而有
。注意到
故
,进而由h的定义可知,对于任意
,有
(5)
定理3.1:设
为m阶n维张量。若对任意的
,
满足
(6)
且对
,存在
,使得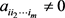 ,则
是
-张量。
,则
是
-张量。
证明:由(6)式知,对对任意的
,
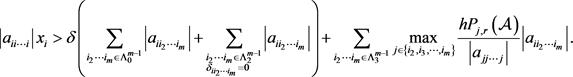
令
(7)
当
时,记
。由(7)式知
,且
从而必有充分小的正数
,使
,且
。
构造正对角矩阵
,记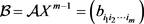 ,其中
,其中
(a) 对
,存在
,使得
,且对任意
,总可以取到充分小的正数 ,使得
,则
,使得
,则
(b) 对
,由 (7)式知
(c) 对
,由(5)式知
综上所述,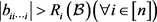 ,即
是严格对角占优的。由引理2.1知
是
-张量,进而由引理2.3知
是
-张量。
,即
是严格对角占优的。由引理2.1知
是
-张量,进而由引理2.3知
是
-张量。
定理3.2:设
为m阶n维张量,
不可约,若对任意的
,
(8)
且(8)中至少有一个严格不等式成立,则
是
-张量。
证明:类似定理3.1的证明方法。由于
是不可约的,则
构造正对角矩阵
,其中
令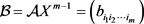 ,则
不可约。类似于定理3.1的证明,可得
,且对
,(8)中至少有一个严格不等式成立,即存在一个
,使得
。由引理2.2知
是
-张量,进而由引理2.3知
也是
-张量。
,则
不可约。类似于定理3.1的证明,可得
,且对
,(8)中至少有一个严格不等式成立,即存在一个
,使得
。由引理2.2知
是
-张量,进而由引理2.3知
也是
-张量。
定理3.3:设
为m阶n维张量。若对任意的
,
且对
,存在从i到j的非零元素链使得 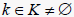 ,则
是
-张量。
,则
是
-张量。
证明:构造正对角矩阵
,记 ,其中
,其中
类似于的定理3.1的证明,可得
,至少存在一个
,使得
。另外,如果
,那么
。假设
中存在一个从i到j非零元素链使得
,那么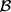 中也存在从i到j的非零元素链使得k满足
。因此,
满足引理2.4的条件,所以
中也存在从i到j的非零元素链使得k满足
。因此,
满足引理2.4的条件,所以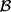 是
-张量,进而由引理2.3知
是
-张量。
是
-张量,进而由引理2.3知
是
-张量。
例3.1:给定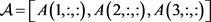 ,其中
,其中
由张量
的元素得到
所以
。计算得
当
时,有
所以张量
满足本文定理3.1的条件,故
是
-张量。但
因此,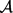 不满足 [15] 中定理1.1的条件。
不满足 [15] 中定理1.1的条件。
4. 应用
在这一节中,基于
-张量的准则,我们提出了偶数阶实对称张量正定的一些新条件(多元形式的正定)。首先,我们给出以下引理:
引理4.1 [13]:设m阶n维张量
为偶数阶实对称张量,对任意的
都满足
。
如果
是
-张量,则
是正定的。
根据引理4.1,定理3.1~3.3,得到以下结果:
定理4.1:设m阶n维张量
为偶数阶实对称张量,对任意的
都满足
。
如果
满足下列条件之一:
i) 定理3.1的所有条件;
ii) 定理3.2的所有条件;
iii) 定理3.3的所有条件;
则
是正定的。
例4.1:设四次齐次多项式
其中
是一个4阶4维的实对称张量,且
其余的
。计算得
因此,
既不是严格对角占优张量也不是拟双严格对角占优张量,所以不能用 [16] 的定理3和 [17] 的定理4来判定
的正定性。但是,可以证明
满足本文定理3.1的条件。因为
所以
。计算得
所以可得,当
时,
根据定理4.1,张量
是正定的,即
是正定的。
5. 结论
本文讨论了
-张量的判定问题,得到了几个新的判定不等式,并给出了其在偶数阶实对称张量,即偶次齐次多项式正定性判定中的应用。数值算例表明了本文所得结论的有效性。
致谢
感谢审稿老师和编辑老师提出了宝贵意见。
基金项目
贵州省科学技术基金(20181079, 20191161),贵州民族大学自然科学基金(GZMU[2019]YB08)。