二层人工神经网络在股市预测模型中的应用——以上证指数为例

Application of Two-Layer Artificial Neural Network in Stock Market Prediction Model—In Case of Shanghai Composite Index

摘要: 文章在阐述了现行的股价指数预测方法基于线性假设的局限性，针对股价指数变动的非线性和波动性，探讨了一种二层人工神经网络的股价指数预测模型。在Python软件的支持下，以上证综合指数(简称上证指数，代码000001) 1050个连续交易日的收盘价为原始样本数据，对指数收盘价及其增长指数进行短期预测，分别计算样本数据和预测数据的涨跌变动趋势。实证结果表明，文中构建的二层结构的BP神经网络预测上证指数变动趋势的准确率高达0.65。得出结论，当样本量和输入层变量选取恰当、网络学习训练次数足够时，使用BP神经网络预测股价指数变动趋势的结果较为准确。

Abstract: In this paper, after expounding the limitations of the current stock index prediction method based on the linear hypothesis, a new stock index prediction model based on the two-layer artificial neural network is discussed, aiming at the nonlinearity and volatility of the stock index, taking the closing price of Shanghai Composite Index (Shanghai Securities Composite Index, code 000001) for 1050 consecutive trading days as the original sample data, then making a short-term prediction of the index closing price and its growth index with the support of Python. Meanwhile, the fluctuation trend of the sample data and the forecast data is calculated respectively. The empirical results show that the accuracy of the two-layer BP neural network is up to 0.65. It is concluded that when the sample size and input layer variables are properly selected and the network learning and training times are sufficient, the BP neural network is more accurate in predicting the trend of stock price index.

1. 引言

近些年来，随着经济的不断发展，证券市场上股票价格的影响因素也就越来越多，股市内外各因素间的相关性错综复杂，诸如自然灾害、突发公共卫生事件等等都可能导致股价的波动且很可能是偶然的、无法预测的。高琴认为股票市场是一个影响因素多、各种不确定性共同作用的局系统，股价的波动往往表现出很强的非线性的特征，使得股市中的数量关系难以提取及定量分析 [1]。吴立扬和周波认为证券分析法中的基础分析虽然有一定的合理性但也常常是以失败告终，而技术分析一开始是实用的，但准确性无法得到保证 [2]。由于计算机和人工智能的发展，人工神经网络技术逐渐成熟并应用于多个领域，也逐渐被应用到股票预测上。刘海玥通过实证分析时间序列模型与人工神经网络在股价预测上的准确性，发现时间序列模型的线性假设影响预测结果的准确性，而后者能够解决样本数据非线性的问题，其结果的准确性更强 [3]。李洪英也认为，人工神经网络作为一种由大量简单神经元广泛互相连接而成的非线性映射或自适应动力系统，能有效解决股价预测中常见的困难 [4]。丁美琳等人发现人工神经网络对非线性关系有很强的非线性逼近能力，可以通过学习股票历史数据寻找其价格规律 [5]。

由于股票指数价格是受多方因素影响的，预测其具体数值的误差可能会很大，而且投资者们更关注的是股价的涨跌趋势而不是其具体价格。因此，本文通过构建二层的BP神经网络，来预测上证指数的涨跌趋势和上证指数累计增长指数的涨跌趋势。

2. 人工神经网络预测模型

人工神经网络(Artificial Neural Network，简称ANN)即神经网络，它的组织能够模拟生物神经系统对真实世界物体所作的交互反应，是理论化的人脑神经网络的数学模型，是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统 [6]，具有高度的并行性、强大的自适应和自学习能力，可以有效预测股票的价格。而BP (Back Propagation)神经网络是目前使用最广泛的一种人工神经网络，通过反向传播的方式，求得模型的最优解。基于BP算法的二层神经网络结构如图1所示。二层BP前馈式神经网由输入层和一个隐含层(同时也为输出层)组成。简单来说，输入神经元组成的一行n列矩阵 $X_n$ 经过一层隐含层赋予的权值，即与权矩阵 $w_{nm}$ 相乘即可获得经过该隐含层后形成的新矩阵，由于是二层的神经网络，所以经过一次权变后形成的新矩阵即为该神经网络的输出矩阵。而BP算法就是指，先是用一个随机的输入矩阵进行尝试得到一个对应的输出矩阵，然后对比该输出矩阵的误差项的大小，然后不断调整输出矩阵，同时向前反馈会得到对应的输入矩阵，直至误差项为零或者最小时，对应的输入矩阵即为该模型的最优解。

Figure 1. BP neural network structure on the second floor

图1. 二层BP神经网络结构图

因为股票指数其实也会受其他非证券因素的影响，为了综合考虑将所有的影响因素所以本文使用的是带常数项的人工神经网络模型，其基本模型就是一个带常数项的非齐次线性方程组见公式(1)。我们要做的就是求得该方程组的最优解，然后再将预测窗口所对应的输入层与最优解进行运算，即可得到预测目标。

$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n+h=y_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n+h=y_2\\ ⋮\\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n+h=y_m\end{array}$ (1)

方程的矩阵表示形式为

$A_{mn}{X}_{n1}+I_{m1}h=Y_{m1}$ (2)

在股票指数预测中 $A_{mn}$ 为做进行模拟的样本数据组成的m行n列的输入矩阵，而 $X_{n1}$ 和h即为所求， $Y_{m1}$ 也是由股票指数样本组成的输出矩阵，求解的过程就是求得一组预测数据和原始数据拟合度最高的最优解，然后再通过该组解和已知输入矩阵求得预测值。

假设股票指数样本序列为

$S=\left\{y_1,y_2,\cdots ,y_n,y_{n+1},\cdots ,y_{n_0},y_{n_0+1},\cdots ,y_N\right\}$ (3)

因此，当我们采用时间序列的向量自回归方法对样本进行模拟预测时，当输入矩阵行数为 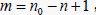，取 $i=0,1,2,\cdots ,m-1$ 时(见图1)，矩阵方程的通项公式为

$y_{i+1}{x}_1+y_{i+2}{x}_2+\cdots +y_{n-1+i}{x}_{n-1}+h=y_{n+i}$ (4)

该模型采用的是一个自循环矩阵，输入矩阵和输出矩阵皆来自同一个样本数据序列，只是在排列序列上有所区别而已。

但是人工神经网络并不是直接求解上述方程，而是通过引入一个激活函数f见式(5)，使得原线性函数变成了一个新的线性函数见式(8)，通过求解新的线性函数从而得到原方程的解。

$f\left(x\right)=\frac{1}{1+{\text{e}}^x}$ (5)

激活函数的定义域为 $x\in \left(-\infty ,+\infty \right)$，值域为 $y\in \left(0,1\right)$，当样本数据超过1时则不能直接使用该激活函数。所以对于一个非负序列 $\left\{y_1,y_2,\cdots ,y_n\right\}$，定义一个上限制 $K>0$，有

$y_i=\frac{y_i}{K},\left(i=1,2,\cdots ,n\right)$ (6)

这样得到的 $y_i\in \left(0,1\right)$，新得到的序列符合激活函数的值域要求。但是求得最优解和到预测值时，结果要进行输出预测值或图示需要进行对应的逆运算见式(7)，还原序列。

$y_i=K{y}_i,\left(i=1,2,\cdots ,n\right)$ (7)

因此，作用了激活函数的模型变为

$f\left(A_{mn}{X}_{n1}+I_{m1}h\right)=Y_{m1}$ (8)

令

$U_{m1}=A_{mn}{X}_{n1}+I_{m1}h$ (9)

则有

$f\left(U_{m1}\right)=Y_{m1}$ (10)

假设 $E_{m1}$ 为误差项，满足关系式：

$E_{m1}=Y_{m1}-f\left(U_{m1}\right)$ (11)

当误差项绝对值最小时则求得最优解，但是BP神经网络并不是直接求解，而是反向求解。假设 $E_{m1}\ne 0$，通过对 $X_{n1}$ 和h分别增加调节量 ${\delta }_{n1}$ 和 $\tau$ ：

$X_{n1}=X_{n1}+{\delta }_{n1}$ (12)

$h=h+\tau$ (13)

则有：

$f\left(A_{mn}\left(X_{n1}+{\delta }_{n1}\right)+I_{m1}\left(h+\tau \right)\right)=f\left(U_{m1}+A_{mn}{\delta }_{n1}+I_{m1}\tau \right)=Y_{m1}$ (14)

则：

$E_{m1}=Y_{m1}-f\left(U_{m1}+A_{mn}{\delta }_{n1}+I_{m1}\tau \right)$ (15)

所以方程式求解变为求式(15)中使得误差项绝对值最小的调节量 ${\delta }_{n1}$ 和 $\tau$。由于本文使用的是二层的神经网络，则按照Taylor展开式对激活函数进行一阶泰勒展式展开，所以：

$f\left(U_{m1}+A_{mn}{\delta }_{n1}+I_{m1}\tau \right)=f\left(U_{m1}\right)+\frac{f^{\prime }\left(U_{m1}\right)}{1!}\left(A_{mn}{\delta }_{n1}+I_{m1}\tau \right)=Y_{m1}$ (16)

则：

$f^{\prime }\left(U_{m1}\right)\left(A_{mn}{\delta }_{n1}+I_{m1}\tau \right)=Y_{m1}-f\left(U_{m1}\right)=E_{m1}$ (17)

所以：

$A_{mn}{\delta }_{n1}+I_{m1}\tau =\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}$ (18)

当 $\tau =0$ 时，则有：

${\delta }_{n1}={\left(A_{mn}^{\text{T}}{A}_{mn}\right)}^{-1}{A}_{mn}^{\text{T}}\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}$ (19)

同理对于常数项的调节量也是同样的方法，有

$\tau ={\left(I_{m1}^{\text{T}}{I}_{m1}\right)}^{-1}{I}_{m1}^{\text{T}}\left\{\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}-A_{mn}{\delta }_{n1}\right\}$ (20)

此时得到的 ${\delta }_{n1}$ 和 $\tau$ 仅是初步的值，为了使得模型的结果最为精确，求得方程的最优解还需要在上述的基础上继续重复逐步地迭代，直至增加了调节量的 $X_{n1}$ 和h能够使方程的误差值最小。这样的迭代方式其实就是机器自学习的过程，通过不断的迭代，在拥有初始解的基础上不断调整调节量，直至经过该调节量调节的方程解集对样本数据的拟合度最高。

3. 数据来源和样本处理

文章从上海证券交易所网站上选取2016年~2020年4月上证指数的收盘价共1050个数据作为全样本数据，对最后的20天指数进行预测并通过对比进行预测效果分析。而在使用Python进行人工神经网络分析的过程中，适当分割样本数据是最优解或最优预测效果的必备条件，假设将1050个数据按照从早到晚的时间顺序进行排序，即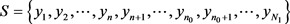， $N_1$ 为1050最大样本数据个数。此外，需注意的是Python的数量计数是从0开始的。

如图2所示，所有样本数据定义为 $N_1$，将该样本数据划分为两个窗口 [7]。

一是样本模拟窗口 $n_0$，本文中为1030。即初始模拟时，建立模型和求得模型最优解所应用到的所有数据，这个区间的样本又可以根据方程中变量的个数划分为两个区间，以n为界限，第一个方程式的输入系数为区间 $\left[1,n-1\right]$，因变量则为序号为n当天的样本值，n往后的 $\left[n,n_0\right]$ 区间的样本值充当过方程式的因变量，即样本模拟时的输出矩阵，该区间的样本值个数也就是整个人工神经网络进行学习时使用的输入矩阵的行数。

二是样本预测窗口 $\left[n_0+1,N_1\right]$，在本文中模型中为最后20个数据即 $\left[1031,1050\right]$ 区间，通过使用样本模拟窗口求得的最优解X和常数项与对应的输入层进行运算即可得到所预测的20天数据。

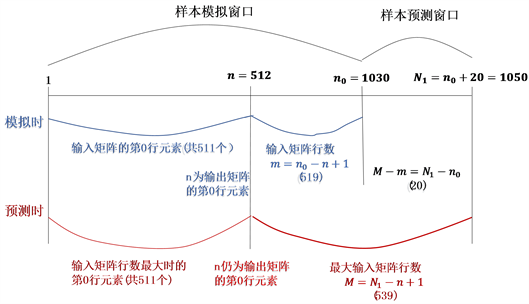
Figure 2. Sample interval division of prediction model

图2. 预测模型的样本区间划分

该预测模型在Python中的应用，先进行理论上程序的编写，然后再导入数据具体运算。基本原理就是，先引入相关函数库，预先定义一个激活函数，然后根据样本模拟窗口 $n_0$ 进行初步模拟，定义自回归激活函数的输入和输出矩阵，选择随机数形成初步的自变量和常数项矩阵，在此基础上定义迭代的步骤，定义迭代的次数，运行程序即可得到固定迭代次数下一组使误差项最小的解 $\left\{x_1,x_2,\cdots ,x_{n-1},h\right\}$ 并输出，并对上述步骤形成的拟合方程式进行误差水平测试。值得注意的是迭代次数的多少需要人工选择，通常迭代次数越高准确率就越高。此外，提高迭代次数不是提高模型预测准确度唯一的办法，可通过调整方程中自变量的个数来提高模型的准确度。然后将样本模拟得到的解集代入到全样本窗口 $N_1$ 下，即可得到 $\left[n,N_1\right]$ 窗口下的预测值，自然就可得到未来20天的预测值。同时进行原样本数据和预测值的趋势变动的一致性与否，若趋势一致则记为成功，计算预测值中成功的比率，即可得出模型预测效果的好坏。

4. 实证分析

由于预测模型预测的股票指数，其价格的波动性很大且难以预测，同时投资者预测指数更多的是为了了解指数价格的未来的涨跌趋势，所以对于预测结果的可行性分析分析其涨跌趋势比预测数偏差更为合理，所以分别计算样本数据序列和预测值序列每一天的环比增长率，然后将两者的对应序列的增长率相乘，见式(21)。若乘积大于零，则证明预测的涨跌趋势一致，预测结果是理想的，预测成功；否则预测趋势与实际变动趋势不一致，预测失败。然后计算预测成功次数在总预测次数中的占比，通过成功率的高低来分析该预测模型预测结果可靠与否。若样本序列为 $\left\{y_t\right\}$，预测值序列为 $\left\{{\hat{y}}_t\right\}$，则有

$Tren{d}_t=\left(\frac{y_t}{y_{t-1}}-1\right)\left(\frac{{\hat{y}}_t}{{\hat{y}}_{t-1}}-1\right)$ (21)

4.1. 上证指数预测

正如上文所提到的，对于取得的股票指数的收盘价预处理就是寻找一个上限制除以这些样本点，让样本数据能够符合激活函数的值域要求，即在 $\left(0,1\right)$ 区间内。由于上证指数的数值基本都在0到5000之间，所以将上限K设为10,000相对合适。此外，模型精确度会受到迭代次数和输入变量个数的影响，因此在迭代次数为100时，比较了方程变量分别为399和511时预测趋势的准确性，结果见表1。发现当方程自变量个数为511时，无论是模拟窗口还是预测窗口的成功的概率都比失败的概率高，因此，选择 $n=512$ 时的模型进行预测。

Table 1. Model prediction success rate of the Shanghai composite index trend

表1. 模型预测上证指数趋势成功的概率

所以将 $n=512$ 时得到的最优解集带入模型，有 $m=n_0-n+1=1030-512+1=519$，即输入矩阵为一个519×511的矩阵，取 $i=0,1,2,\cdots ,538$，所以预测模型的通项公式可以表示为：

$-1.605346y_{i+1}+0.77312y_{i+2}+\cdots +3.871329y_{n-1+i}+0.006184=y_{n+i}$ (22)

表2为该二层BP神经网络对上证指数预测结果拟合度的误差水平检验结果，该模型的R值为0.9976，误差的分布离散度和误差平方和较小，证明该模型解释力度强、拟合效果好。

图3全样本窗口拟合的效果图，从图像来看前期模拟时的样本点基本都在拟合曲线上的，这也证明模型的拟合预测效果具有一定的可靠性。但是，到了后20天的预测值与实际数值有较大的偏离程度，预测值的波动幅度比实际样本值更大，这很可能是因为我们进行预测的这20天并没有参与到样本模拟

Table 2. Error level test of Shanghai composite index fitting model

表2. 上证指数拟合模型的误差水平检验

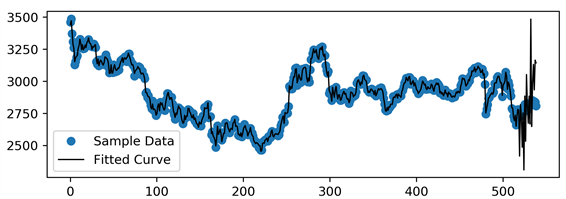
Figure 3. Fitting curve: Shanghai composite index model full sample simulation window

图3. 上证指数全样本模拟窗口拟合效果图

时的模型中，机器学习时并没有学习到这部分数据，模型使用的最优解也并不是全样本区间模拟得到的最优解，因此预测未来20天时的数据存在较大偏差是可理解的。但是对于股市来说更重要的是价格的涨跌趋势，所以与其说该人工神经网络预测了指数的价格，不如说是预测了指数价格的变动趋势，结果证明该模型在指数变动趋势上还是有很强的准确性的。这也正是人工神经网络的一大优势，具有极强的容错能力和学习能力。即便未来20天的数据没有参与机器学习，但是模拟得到的模型仍然具有很强的解释性。

图4更仔细的展示了样本预测窗口的预测值和实际值。如果仅仅只是从预测数值的准确性和误差离散度来看，其实对于未来20天的股票指数价格的预测误差还是比较大的，如果预测其他数据出现这种程度的偏差可能解释力度较差。但是对于股票指数价格来说，预测与实际的涨跌趋势是否一致才是评判一个股价预测模型准确性的重要标准。从图5预测的涨跌幅度来看，预测的准确性比较高的，20天内有7天预测趋势有误，成功率高达0.65。

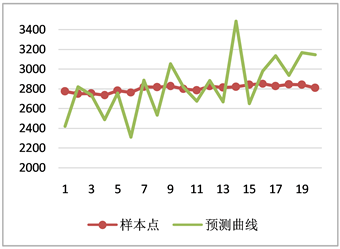
Figure 4. Comparison chart: actual value and forecast value

图4. 上证指数实际值与预测值对比图

Figure 5. Index up and down trend chart

图5. 上证指数涨跌趋势图

4.2. 上证指数增长指数预测

此处使用的上证指数的增长指数为上证指数价格的累计增长率，即每一天的股票指数与样本中的基期的比值，在本例中的基期为按时间序列排序的第一个数据，即2016年1月4日的上证指数的收盘价格。假设基期的股票指数价格为 $y_0$ 第i天的股票指数价格为 $y_i$，其增长指数为 $e_i$，则有

$e_i=\frac{y_i}{y_0},\left(i=0,1,2,\cdots ,N_1\right)$ (23)

对于取得的股票指数的增长指数的预处理就是寻找一个上限制除以这些样本点，使的样本数据能够符合激活函数的值域要求，即在 $\left(0,1\right)$ 区间内。由于增长指数的数值基本都在0到2之间，所以将上限K设为2较为合理。由表3可知，当方程自变量的个数为511时，模拟窗口和预测窗口中预测到的股票指数涨跌变动趋势成功率比自变量为399个时高，尤其是预测窗口中的成功率。因此，选择 $n=512$ 时的模型和最优解进行预测。

Table 3. Model prediction success rate of growth index trend

表3. 预测模型预测上证指数增长指数趋势成功的概率

所以将 $n=512$ 时得到的最优解集带入模型，有 $m=n_0-n+1=1030-512+1=519$，即输入矩阵 $A_{mn}$ 为519 × 512的矩阵，取 $i=0,1,2,\cdots ,538$，所以预测模型可表示为：

$-1.144764y_{i+1}+0.634725y_{i+2}+\cdots +3.436624y_{n-1+i}+0.00201=y_{n+i}$ (24)

表4为该二层BP神经网络对上证指数预测结果拟合度的误差水平检验结果，该模型的R值为0.9977，误差的分布离散度和误差平方和都在0.03以内相对较小，因此该模型解释力度强、拟合效果好。图6为增长指数预测结果的拟合曲线，可以直接观察到该预测模型对样本数据的解释力度较强，样本点基本在拟合曲线上。而预测窗口如上文所说，由于没有参与机器学习，所以在预测值上可能会有较大幅度的波动。

图7清晰地反应了预测窗口中未来20天样本点与拟合曲线的拟合程度，预测值的变动幅度大于实际

Table 4. Error level test of growth index fitting model

表4. 上证指数增长指数模型拟合的误差水平检验结果

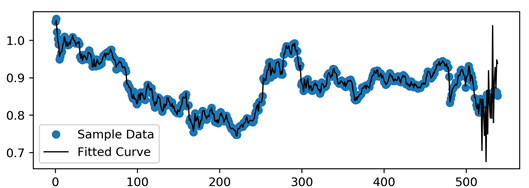
Figure 6. Fitting curve: growth index model full sample simulation window

图6. 上证指数增长指数全样本模拟窗口拟合效果图

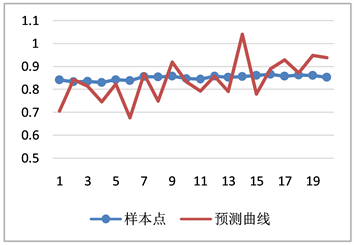
Figure 7. Comparison chart: actual value and forecast value

图7. 上证指数增长指数实际值与预测值对比图

Figure 8. Growth index up and down trend chart

图8. 上证指数增长指数涨跌趋势图

值。尽管预测结果在数值上可能存在较大的偏离程度，但是对于指数来说更关注的是未来的增长或下降的趋势。如图8所示，在未来20天内，只有7天趋势值为负数，即预测涨跌趋势失败，成功概率也能达到0.65，因此该模型预测在预测上证指数价格的增长指数上也是有效的。

5. 结论

本文在明晰了传统股票价格预测模型的局限性和股价预测的困难度后，提出了使用二层BP神经网络来预测股票价格。人工神经网络以其强大的容错、纠错和学习能力，能够对一些具有高强度非线性关系的数值进行预测。从上文中运用模型对上证指数进行预测的效果来看，运用二层BP神经网络可以预测股票价格，这为股价预测提供了又一种行之有效的方法。但是，使用该模型进行预测时，预测效果在很大程度上会受到引入方程变量和预先设置的机器学习次数的影响，当出现效果不理想时可以调整方程的变量个数或者迭代次数。值得注意的是，使用人工神经网络预测股价评判其效果更应当参考其在预测股价涨跌趋势上的准确性而不是具体价格的离散度。

致谢

在此，我要由衷地感谢厦门国家会计学院的阎虎勤老师，是他的课程让我发现了Python的魅力所在，也学习到了很多的实证分析模型，为完成本文的撰写工作奠定了理论基础。在撰写过程中，老师在选题、文章框架和内容上提供了许多宝贵的意见。此外，我还要感谢一直支持我的家人和朋友们，是他们的鼓励和陪伴给予了我奋发向上的动力。