正多面体的七种不同类型的着色公式

doi:10.12677/PM.2020.105066

期刊菜单

正多面体的七种不同类型的着色公式
Seven Different Types of Coloring Formulas for Regular Polyhedrons

DOI: 10.12677/PM.2020.105066, PDF, HTML, XML,
作者: 肖仁兵：云南师范大学数学学院，云南昆明
关键词: 正多面体；旋转群；着色公式；Pólya定理；Regular Polyhedron； Rotation Group； Coloring Formula； Pólya Theorem

摘要: 本文我们研究正多面体的顶点、边、面、点边、点面、边面和点边面的着色公式。我们通过考虑正多面体的自同构群(旋转群)在正多面体点、边、面等个体集合上的作用，先求出所有正多面体的旋转群，进而得到这些旋转群在正多面体点、边、面等个体集合上的诱导作用及旋转群中元素的置换类型及个数，然后利用Pólya定理得出正多面体的顶点、边、面、点边、点面、边面和点边面的着色公式。

Abstract: In this paper we obtain the coloring formulas of vertex, edge, surface, point edge, point surface, edge surface, and point edge surface of regular polyhedrons by using Pólya theorem. Our method is to use the knowledge of permutation groups. First we determine the rotation groups of all regular polyhedrons, and then we determine the permutation types and the numbers of elements in the induced permutation groups. Then the formulas are obtained by considering the actions of the groups on the set.

文章引用：肖仁兵. 正多面体的七种不同类型的着色公式[J]. 理论数学, 2020, 10(5): 540-548. https://doi.org/10.12677/PM.2020.105066

1. 引言

图着色问题是图论和组合数学中的一个经典问题，着色问题的研究极大地促进了图论和组合数学的发展。近年来，用代数方法研究图着色问题是解决这一古老问题的重要途径。所谓正多面体的顶点着色问题如下：用m种颜色给对一个正多面体的顶点着色，如果两种着色方法经过对正多面体进行一次对称旋转能互相重合，则认为这两种着色本质上是一样的，问本质上有多少种不同的着色？定义详见文献 [1]，同时文献 [1] 中还给出了正六面体的着色公式。此外叶载良，韩冬在文献 [2] 中利用Burnside定理给出了其它四种正多面体的顶点着色公式，本文我们利用Pólya定理给出五种正多面体的顶点、边、面、点边、点面、边面和点边面的着色公式。

2. 预备知识

这一节中我们先给出本文需要的一些预备知识，本文中涉及图着色的概念可参见文献 [1]，涉及置换群与群作用的概念和内容可参见文献 [3]。

定义1.1 [4] 设A是一个n元集，G是A上的一个置换群， $g \in G$ ，如果g的轮换分解式中含有 $b_{i} (i = 1, 2, \dots, n)$ 个长为i的轮换( $b_{1} + 2 b_{2} + \dots + n b_{n} = n$ )，则称g是一个型为( $b_{1}, b_{2}, \dots, b_{n}$ )的n元置换，或称g是一个型为 $1^{b_{1}} 2^{b_{2}} \dots n^{b_{n}}$ 的n元置换。

定义1.2 [4] 设G是n元集A上的一个置换群， $x_{1}, x_{2}, \dots, x_{n}$ 是n个未定元，对每个 $g \in G$ ，以 $b_{i} (g)$ ( $i = 1, 2, \dots, n$ )表示g的轮换分解式所含有的长为i的轮换的个数，令

$P_{G} (x_{1}, x_{2}, \dots, x_{n}) = \frac{1}{| G |} \sum_{g \in G} x_{1}^{b_{1} (g)} x_{2}^{b_{2} (g)} \dots x_{n}^{b_{n} ( g )}$

$P_{G} (x_{1}, x_{2}, \dots, x_{n})$ 称为A上的置换群(G，。)的轮换指标。

定理1 (Pólya定理) [5] 设有限群作用在n个对象组成的集合W上。G中元素g在上的置换表示记作 $\hat{g}$ 。用m种颜色给W里的n个对象染色，则真正不同的染色方案的个数r为：

$r = \frac{1}{| G |} \sum_{g \in G} m^{r ( g ^ )}$

其中 $r (\hat{g})$ 是 $\hat{g}$ 的轮换表示中轮换的个数(包括1-轮换)。

定理2 (Burnside引理) [5] 设有限群G在有限集合Ω上有一个作用，用F(g)表示g的不动点集，即

$F (g) = 〈 x \in Ω | g \circ x = x 〉$

则轨道条数r为

$r = \frac{1}{| G |} \sum_{g \in G} | F (g) |$

即轨道条数等于平均被G的一个元素保持不动的点的数目。

参考文献 [6]，三维空间中总共有五个正多面体，分别为：正四面体、正六面体、正八面体、正十二面体和正二十面体，具体如下表1。

Table 1. Number of vertices, sides, number of faces and shape of regular polyhedron

表1. 正多面体的顶点数，边数，面数和面的形状

3. 主要结果

我们的讨论的主要依赖于对正多面体的旋转轴的分类。下面我们依次对正四面体、正六面体、正八面体、正十二面体、正二十面体确定其旋转轴的类型，然后确定在相应子图上的诱导作用，最后利用Pólya定理得到这些正多面体的着色公式。

1) 正四面体：由表1知正四面体的顶点数、边数及面数分别为4，6，4。图形结构如图1所示。我们给图形顶点标上数字标号，4个顶点如图依次记为1，2，3，4；6条边依次记为： $e_{1} (1 2)$ ， $e_{2} (1 3)$ ， $e_{3} (1 4)$ ， $e_{4} (2 3)$ ， $e_{5} (2 4)$ ， $e_{6} (3 4)$ 。4个面依次记为： $u_{1} (123)$ ， $u_{2} (124)$ ， $u_{3} (134)$ ， $u_{4} (2 3 4)$ 。

Figure 1. Regular tetrahedron structure diagram

图1. 正四面体结构图

正四面体的旋转轴可分为两类：

I类为过一顶点与底面中心的连线为轴，旋转120˚和240˚，取旋转群中元素为通过顶点1和其对面 $u_{4} (2 3 4)$ 中心的连线旋转120˚，其点置换 $(1)$ $(2 3 4)$ 是1¹3¹型置换，对应的边置换为 $(e_{1} e_{2} e_{3})$ $(e_{4} e_{6} e_{5})$ 是3²型置换，对应的面置换为 $(u_{4})$ $(u_{1} u_{2} u_{3})$ 是1¹3¹型置换，有四条类似轴，两种转角，共8个元素；

Ⅱ类为过两条对边中点连线的轴，旋转180˚，以 $e_{1} (1 2)$ 与其对边 $e_{6} (3 4)$ 的中点连线为轴旋转180˚为例，其点置换 $(1 2)$ $(3 4)$ 是2²型置换，求得对应的边置换为 $(e_{1})$ $(e_{6})$ $(e_{2} e_{5})$ $(e_{3} e_{4})$ 是1²2²型置换，对应的面置换为 $(u_{1} u_{2})$ $(u_{3} u_{4})$ 是2²型置换，有三组对边，一种转角，共3个元素。

加上单位元，点置换群 $V_{4}$ 有1⁴型1个，1¹3¹型8个，2²型3个；边置换群 $E_{4}$ 有1⁶型1个，3²型8个，1²2²型3个；面置换群 $U_{4}$ 有1⁴型1个，1¹3¹型8个，2²型3个；对每个类型置换计算不动点数，由Pólya定理即可得到正四面体的m种颜色的顶点、边、面着色公式为：

$N_{V_{4}} = \frac{1}{12} (m^{4} + 11 m^{2})$ , $N_{E_{4}} = \frac{1}{12} (m^{6} + 3 m^{4} + 8 m^{2})$ , $N_{U_{4}} = \frac{1}{12} (m^{4} + 11 m^{2})$

如果我们考虑正四面体旋转群G作用在包含正四面体顶点和边的集合 $W = {1, 2, 3, 4, e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}}$ 上，导出的群称为点边置换群 $V E_{4}$ ，则I类旋转为过一顶点与底面中心的连线为轴，旋转120˚和240˚，取G中元素 $g_{1}$ 为通过顶点1和其对面u₄ (2 3 4)中心的连线旋转120˚，作用在集合W上，得到的置换表示称为点边置换，得到 ${\hat{g}}_{1} = (1) (2 3 4)$ $(e_{1} e_{2} e_{3})$ $(e_{4} e_{6} e_{5})$ 是1¹3³型置换，有四条类似轴，两种转角，共8个元素；II类旋转为过两条对边中点连线的轴，旋转180˚，取G中元素 $g_{2}$ 为以 $e_{1} (1 2)$ 与其对边 $e_{6} (3 4)$ 的中点连线为轴旋转180˚，得到 ${\hat{g}}_{2} = (1 2) (3 4)$ $(e_{1})$ $(e_{6})$ $(e_{2} e_{5})$ $(e_{3} e_{4})$ 是1²2⁴型置换，有三组对边，一种转角，共3个元素；加上单位元，则点边置换群 $V E_{4}$ 有1¹⁰型1个，1¹3³型8个，1²2⁴型3个。由Pólya定理即可得到正四面体的m种颜色的点边着色公式为：

$N_{V E_{4}} = \frac{1}{12} (m^{10} + 3 m^{6} + 8 m^{4})$

所以我们可以类似的得出正四面体的点面置换群 $V U_{4}$ 有1⁸型1个，1²3²型8个，2⁴型3个；边面置换群 $E U_{4}$ 有1¹⁰型1个，1¹3³型8个，1²2⁴型3个；点边面置换群 $V E U_{4}$ 有1¹⁴型1个，1²3⁴型8个，1²2⁶型3个；由Pólya定理即可得到正四面体的m种颜色的点面、边面和点边面着色公式分别为：

$N_{V U_{4}} = \frac{1}{12} (m^{8} + 11 m^{4})$ , $N_{E U_{4}} = \frac{1}{12} (m^{10} + 3 m^{6} + 8 m^{4})$ , $N_{V E U_{4}} = \frac{1}{12} (m^{14} + 3 m^{8} + 8 m^{6})$

2) 正六面体：由表1知正六面体的顶点数、边数及面数分别为8，12，6。图形结构如图2所示。我们给图形顶点标上数字标号，8个顶点如图依次记为 $1, 2, \dots, 8$ 表示。12条边依次记为： $e_{1} (1 2)$ ， $e_{2} (2 3)$ ， $e_{3} (3 4)$ ， $e_{4} (1 4)$ ， $e_{5} (5 6)$ ， $e_{6} (6 7)$ ， $e_{7} (7 8)$ ， $e_{8} (5 8)$ ， $e_{9} (1 5)$ ， $e_{10} (2 6)$ ， $e_{11} (3 7)$ ， $e_{12} (4 8)$ 。6个面依次记为： $u_{1} (1 2 3 4)$ ， $u_{2} (5 6 7 8)$ ， $u_{3} (1 2 5 6)$ ， $u_{4} (3 4 7 8)$ ， $u_{5} (1 4 5 8)$ ， $u_{6} (2 3 6 7)$ 。

Figure 2. Regular hexahedron structure diagram

图2. 正六面体结构图

正六面体的旋转轴可分为三类：

I类为过对面中心的连线为轴，旋转90˚、180˚和270˚，(a) 取旋转群中元素为通过面 $u_{1} (1 2 3 4)$ 和其对面 $u_{2} (5 6 7 8)$ 中心的连线旋转90˚，其点置换 $(1 2 3 4)$ $(5 6 7 8)$ 是4²型置换，边置换为 $(e_{1} e_{2} e_{3} e_{4})$ $(e_{5} e_{6} e_{7} e_{8})$ $(e_{9} e_{10} e_{11} e_{12})$ 是4³型置换，对应的面置换为 $(u_{1})$ $(u_{2})$ $(u_{3} u_{6} u_{4} u_{5})$ 是1²4¹型置换，有三组对面，90˚、270˚两种转角，共6个元素；(b) 取旋转群中元素为通过面 $u_{1} (1 2 3 4)$ 和其对面 $u_{2} (5 6 7 8)$ 中心的连线旋转180˚时，其点置换 $(1 3)$ $(2 4)$ $(5 7)$ $(6 8)$ 是2⁴型置换，边置换为 $(e_{1} e_{3})$ $(e_{2} e_{4})$ $(e_{5} e_{7})$ $(e_{6} e_{8})$ $(e_{9} e_{11})$ $(e_{10} e_{12})$ 是2⁶型置换，对应的面置换为 $(u_{1})$ $(u_{2})$ $(u_{3} u_{4})$ $(u_{5} u_{6})$ 是1²2²型置换，有三组对面，180˚两种转角，共3个元素；

II类为过对角点连线为轴，旋转120˚和240˚，取旋转群中元素为 $(1 7)$ 为对角点的连线为轴顺时针旋转120˚，其点置换 $(1)$ $(7)$ $(2 4 5)$ $(3 8 6)$ 是1²3²型置换，诱导出对应的边置换为 $(e_{1} e_{4} e_{9})$ $(e_{6} e_{11} e_{7})$ $(e_{2} e_{12} e_{5})$ $(e_{3} e_{8} e_{10})$ 是3⁴型置换，对应的面置换为 $(u_{1} u_{5} u_{3})$ $(u_{2} u_{6} u_{4})$ 是3²型置换，有六组对角点，120˚和240˚两种转角，共8个元素；

III类为对边中点的连线为旋转轴，旋转180˚，取旋转群中元素为边 $e_{9} (1 5)$ 和其对边 $e_{11} (3 7)$ 中点连线为轴旋转180˚，其点置换 $(1 5)$ $(3 7)$ $(2 8)$ $(4 6)$ 是2⁴型置换，诱导出对应的边置换 $(e_{9})$ $(e_{11})$ $(e_{1} e_{8})$ $(e_{2} e_{7})$ $(e_{3} e_{6})$ $(e_{4} e_{5})$ $(e_{10} e_{12})$ 是1²2⁵型置换，对应的面置换为 $(u_{1} u_{2})$ $(u_{3} u_{5})$ $(u_{4} u_{6})$ 是2³型置换，有6组对边，1种转角，共6个元素。

加上单位元，点置换群有1⁸型1个，1²3²型8个，4²型6个，2⁴型9个；边置换群有1¹²型1个，3⁴型8个，4³型6个，2⁶型3个，1²2⁵型6个；面置换群有1⁶型1个，3²型8个，1²4¹型6个，1²2²型3个，2³型6个；对每个类型置换计算不动点数，由Pólya定理即可得到正六面体的m种颜色的点、边和面着色公式分别为：

, $N_{E_{6}} = \frac{1}{24} (m^{12} + 6 m^{7} + 3 m^{6} + 8 m^{4} + 6 m^{3})$ ,

$N_{U_{6}} = \frac{1}{24} (m^{6} + 3 m^{4} + 12 m^{3} + 8 m^{2})$

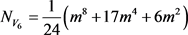由点、边、面的置换群类型及个数，可得出正六面体的点边置换群 $V E_{6}$ 有1²⁰型1个，4⁵型6个，2¹⁰型3个，1²3⁶型8个，1²2⁹型6个；点面置换群 $V U_{6}$ 有1¹⁴型1个，1²4³型6个，1²3⁴型8个，1²2⁶型3个，2⁷型6个；边面置换群 $E U_{6}$ 有1¹⁸型1个，1²4⁴型6个，1²2⁸型9个，3⁶型8个；点边面置换群 $V E U_{6}$ 有1²⁶型1个，1²4⁶型6个，1²2¹²型9个，1²3⁸型8个；由Pólya定理即可得到正六面体的m种颜色的点边、点面、边面和点边面着色公式分别为：

$N_{V E_{6}} = \frac{1}{24} (m^{20} + 6 m^{11} + 3 m^{10} + 8 m^{8} + 6 m^{5})$ , $N_{V U_{6}} = \frac{1}{24} (m^{14} + 3 m^{8} + 6 m^{7} + 8 m^{6} + 6 m^{5})$

$N_{E U_{6}} = \frac{1}{24} (m^{18} + 9 m^{10} + 14 m^{6})$ , $N_{V E U_{6}} = \frac{1}{24} (m^{26} + 9 m^{14} + 8 m^{10} + 6 m^{8})$

3) 正八面体：由表1知正八面体的顶点数、边数及面数分别为6，12，8。图形结构如图3所示。我们给图形顶点标上数字标号，6个顶点如图依次记为 $1, 2, \dots, 6$ 。12条边依次记为: $e_{1} (1 3)$ ， $e_{2} (1 4)$ ， $e_{3} (1 5)$ ， $e_{4} (1 6)$ ， $e_{5} (2 3)$ ， $e_{6} (2 4)$ ， $e_{7} (2 5)$ ， $e_{8} (2 6)$ ， $e_{9} (3 4)$ ， $e_{10} (4 5)$ ， $e_{11} (5 6)$ ， $e_{12} (3 6)$ 。8个面依次记为： $u_{1} (1 3 4)$ ， $u_{2} (1 4 5)$ ， $u_{3} (1 5 6)$ ， $u_{4} (1 3 6)$ ， $u_{5} (2 3 4)$ ， $u_{6} (2 4 5)$ ， $u_{7} (2 5 6)$ ， $u_{8} (2 3 6)$ 。

正八面体的轴旋转可分为三类：

I类为过对面中心的连线为轴，旋转120˚和240˚，取旋转群中元素为通过面 $u_{1} (1 3 4)$ 和其对面 $u_{7} (2 5 6)$ 中心的连线为轴旋转120˚，其点置换 $(1 3 4)$ $(2 5 6)$ 是3²型置换，诱导出对应的边置换为 $(e_{1} e_{9} e_{2})$ $(e_{7} e_{11} e_{8})$ $(e_{3} e_{12} e_{6})$ $(e_{4} e_{5} e_{10})$ 是3⁴型置换，对应的面置换为 $(u_{1})$ $(u_{7})$ $(u_{2} u_{4} u_{5})$ $(u_{3} u_{8} u_{6})$ 是1²3²型置换，有四组对面，两种转角，共8个元素；

II类为过对顶点的连线为轴，旋转90˚、180˚和270˚，(a) 取旋转群中元素为(1 2)为对顶点的连线为轴顺时针旋转90˚，其点置换 $(1)$ $(2)$ $(3 4 5 6)$ 是1²4¹型置换，诱导出对应的边置换为 $(e_{1} e_{2} e_{3} e_{4})$ $(e_{5} e_{6} e_{7} e_{8})$ $(e_{9} e_{10} e_{11} e_{12})$ 是4³型置换，对应的面置换为 $(u_{1} u_{2} u_{3} u_{4})$ $(u_{5} u_{6} u_{7} u_{8})$ 是4²型置换，有三组对顶点，90˚和270˚两种转角，共6个元素；(b) 以 $(1 2)$ 为对顶点的连线为轴旋转180˚为例，其点置换 $(1)$ $(2)$ $(3 5)$ $(4 6)$ 是1²2²型置换，对应的边置换为 $(e_{1} e_{3})$ $(e_{2} e_{4})$ $(e_{5} e_{7})$ $(e_{6} e_{8})$ $(e_{9} e_{11})$ $(e_{10} e_{12})$ 是2⁶型置换，对应的面置换为 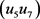$(u_{1} u_{3})$ $(u_{2} u_{4})$ $(u_{6} u_{8})$ 是2⁴型置换，有三组对顶点，一种转角，共3个元素；

Figure 3. Regular octahedral structure

图3. 正八面体结构图

III类为对边中点的连线为旋转轴，旋转180˚，取旋转群中元素为边 $e_{12} (3 6)$ 和其对边 $e_{10} (4 5)$ 的中点连线为轴旋转180˚，则其点置换 $(3 6)$ $(4 5)$ $(1 2)$ 是2³型置换，诱导出对应的边置换 $(e_{10})$ $(e_{12})$ $(e_{1} e_{8})$ $(e_{2} e_{7})$ $(e_{3} e_{6})$ $(e_{4} e_{5})$ $(e_{9} e_{11})$ 是1²2⁵型置换，诱导出对应的面置换为 $(u_{1} u_{7})$ $(u_{2} u_{6})$ $(u_{3} u_{5})$ $(u_{4} u_{8})$ 是2⁴型置换，有6组对边，1种转角，共6个元素。

加上单位元，点置换群有1⁶型1个，3²型8个，1²4¹型6个，1²2²型3个，2³型6个；边置换群有1¹²型1个，3⁴型8个，4³型6个，2⁶型3个，1²2⁵型6个；面置换群有1⁸型1个，1²3²型8个，4²型6个，2⁴型9个；对每个类型置换计算不动点数，由Pólya定理即可得到正八面体的m种颜色的顶点、边、面着色公式为：

$N_{V_{8}} = \frac{1}{24} (m^{6} + 3 m^{4} + 12 m^{3} + 8 m^{2})$ , $N_{E_{8}} = \frac{1}{24} (m^{12} + 6 m^{7} + 3 m^{6} + 8 m^{4} + 6 m^{3})$ ,

$N_{U_{8}} = \frac{1}{24} (m^{8} + 17 m^{4} + 6 m^{2})$

由点、边、面的置换群类型及个数，可得出正八面体的点边置换群 $V E_{8}$ 有1¹⁸型1个，1²4⁴型6个，1²2⁸型9个，3⁶型8个；点面置换群 $V U_{8}$ 有1¹⁴型1个，1²4³型6个，1²3⁴型8个，1²2⁶型3个，2⁷型6个；边面置换群 $E U_{8}$ 有1²⁰型1个，4⁵型6个，2¹⁰型3个，1²3⁶型8个，1²2⁹型6个；点边面置换群 $V E U_{8}$ 有1²⁶型1个，1²4⁶型6个，1²2¹²型9个，1²3⁸型8个；由Pólya定理即可得到正八面体的m种颜色的点边、点面、边面和点边面着色公式分别为：

$N_{V E_{8}} = \frac{1}{24} (m^{18} + 9 m^{10} + 14 m^{6})$ , $N_{V U_{8}} = \frac{1}{24} (m^{14} + 3 m^{8} + 6 m^{7} + 8 m^{6} + 6 m^{5})$

$N_{E U_{8}} = \frac{1}{24} (m^{20} + 6 m^{11} + 3 m^{10} + 8 m^{8} + 6 m^{5})$ , $N_{V E U_{8}} = \frac{1}{24} (m^{26} + 9 m^{14} + 8 m^{10} + 6 m^{8})$

4) 正十二面体：由表1知正十二面体的顶点数、边数及面数分别为20，30，12。图形结构如图4所示。我们给图形顶点标上数字标号，20个顶点如图依次记为 $1, 2, \dots, 20$ 。30条边依次记为： $e_{1} (1 2)$ ， $e_{2} (18 19)$ ， $e_{3} (2 3)$ ， $e_{4} (19 20)$ ， $e_{5} (34)$ ， $e_{6} (16 20)$ ， $e_{7} (45)$ ， $e_{8} (16 17)$ ， $e_{9} (5 1)$ ， $e_{10} (17 18)$ ， $e_{11} (2 7)$ ， $e_{12} (14 19)$ ， $e_{13} (16)$ ， $e_{14} (13 18)$ ， $e_{15} (5 10)$ ， $e_{16} (17 12)$ ， $e_{17} (4 9)$ ， $e_{18} (11 16)$ ， $e_{19} (3 8)$ ， $e_{20} (15 20)$ ， $e_{21} (6 11)$ ， $e_{22} (9 13)$ ， $e_{23} (6 15)$ ， $e_{24} (8 13)$ ， $e_{25} (15 10)$ ， $e_{26} (8 12)$ ， $e_{27} (14 10)$ ， $e_{28} (7 12)$ ， $e_{29} (9 14)$ ， $e_{30} (7 11)$ 。12个面依次记为： $u_{1} (1 2 3 4 5)$ ， $u_{2} (16 17 18 19 20)$ ， $u_{3} (1 2 7 6 11)$ ， $u_{5} (13 18 19 14 9)$ ， $u_{5} (1 5 10 15 6)$ ， $u_{6} (8 12 17 18 13)$ ， $u_{7} (5 4 9 14 10)$ ， $u_{8} (7 11 16 17 12)$ ， $u_{9} (3 4 9 13 8)$ ， $u_{10} (16 20 15 6 11)$ ， $u_{11} (2 3 8 12 7)$ ， $u_{12} (10 14 19 20 15)$ 。

Figure 4. Regular dodecahedron structure diagram

图4. 正十二面体结构图

正十二面体的旋转轴可分为三类：

I类为过对面中心的连线为旋转轴，旋转72˚、144˚、216˚和288˚，取正十二面体旋转群中元素为通过面 $u_{1} (1 2 3 4 5)$ 和其对面 $u_{2} (16 17 18 19 20)$ 的中心的连线为轴旋转72˚，则其点置换 $(1 2 3 4 5)$ $(6 7 8 9 10)$ $(11 12 13 14 15)$ $(16 17 18 19 20)$ 是5⁴型置换，诱导出对应的边置换为 $(e_{1} e_{3} e_{5} e_{7} e_{9})$ $(e_{2} e_{4} e_{6} e_{8} e_{10})$ $(e_{11} e_{19} e_{17} e_{15} e_{13})$ $(e_{12} e_{20} e_{18} e_{16} e_{14})$ $(e_{21} e_{28} e_{24} e_{29} e_{25})$ $(e_{30} e_{26} e_{22} e_{27} e_{23})$ 是5⁶型置换，对应的面置换为 $(u_{1})$ $(u_{2})$ $(u_{3} u_{11} u_{9} u_{7} u_{5})$ $(u_{4} u_{12} u_{10} u_{8} u_{6})$ 是1²5²型置换，有六组对面，四种转角，共24个元素；

II类为过对角点连线为轴，旋转120˚和240˚，取旋转群中元素为(6 13)对顶点连线为轴旋转120˚，点置换 $(6)$ $(13)$ $(1 11 15)$ $(5 7 20)$ $(3 14 17)$ $(10 12 16)$ $(8 9 18)$ $(4 12 19)$ 1²3⁶型置换，边置换 $(e_{1} e_{18} e_{25})$ $(e_{2} e_{17} e_{16})$ $(e_{3} e_{8} e_{27})$ $(e_{4} e_{7} e_{28})$ $(e_{5} e_{16} e_{12})$ $(e_{6} e_{15} e_{11})$ $(e_{9} e_{30} e_{20})$ $(e_{19} e_{10} e_{29})$ $(e_{13} e_{21} e_{23})$ $(e_{14} e_{22} e_{24})$ 是3¹⁰型置换，边置换为 $(u_{1} u_{9} u_{7} u_{5} u_{3})$ $(u_{2} u_{10} u_{8} u_{6} u_{4})$ $(u_{18} u_{11} u_{15} u_{19} u_{14})$ $(u_{20} u_{13} u_{17} u_{12} u_{10})$ 是5⁴型置换，有十组对顶点，两种转角，共20个元素；

III类为对边中点的连线为旋转轴，旋转180˚，取旋转群中元素边 $e_{1} (1 2)$ 和其对边 $e_{4} (19 20)$ 中点连线为轴旋转180˚，其点置换 $(1 2)$ $(19 20)$ $(3 5)$ $(4 6)$ $(7 8)$ $(9 11)$ $(10 12)$ $(13 14)$ $(15 17)$ $(16 18)$ 是2¹⁰型置换，类似可得对应的边置换是1²2¹⁴型置换，求得对应的面置换为是2⁶型置换，有15组对边，一种转角，共15个元素。

加上单位元，点置换群有1²⁰型1个，1²3⁶型20个，5⁴型24个，2¹⁰型15个；边置换群有1³⁰型1个，3¹⁰型20个，5⁶型24个，1²2¹⁴型15个；面置换群有1¹²型1个，3⁴型20个，1²5²型24个，2⁶型15个对每个类型置换计算不动点数，由Pólya定理即可得到正二十面体的m种颜色的顶点、边、面着色公式为：

$N_{V_{12}} = \frac{1}{60} (m^{20} + 15 m^{10} + 20 m^{8} + 24 m^{4})$ , $N_{E_{12}} = \frac{1}{60} (m^{30} + 15 m^{16} + 20 m^{10} + 24 m^{6})$ ,

$N_{U_{12}} = \frac{1}{60} (m^{12} + 15 m^{6} + 44 m^{4})$

由点、边、面的置换群类型及个数，可得出正十二面体的点边置换群 $V E_{12}$ 有1⁵⁰型1个，1²3¹⁶型20个，5¹⁰型24个，1²2²⁴型15个；点面置换群 $V U_{12}$ 有1³²型1个，1²3¹⁰型20个，1²5⁶型24个，1²5⁶型20个，2¹⁶型15个；边面置换群 $E U_{12}$ 有1⁴²型1个，3¹⁴型20个，1²5⁸型24个，1²2²⁰型15个；点边面置换群 $V E U_{12}$ 有1⁶²型1个，1²5¹²型24个，1²3²⁰型20个，1²2³⁰型15个；由Pólya定理即可得到正二十面体的m种颜色的点边、点面、边面和点边面着色公式分别为：

$N_{V E_{12}} = \frac{1}{60} (m^{50} + 15 m^{26} + 20 m^{18} + 24 m^{10})$ , $N_{V U_{12}} = \frac{1}{60} (m^{32} + 15 m^{16} + 20 m^{12} + 24 m^{8})$

$N_{E U_{12}} = \frac{1}{60} (m^{42} + 15 m^{22} + 20 m^{14} + 24 m^{10})$ , $N_{V E U_{12}} = \frac{1}{60} (m^{62} + 15 m^{32} + 20 m^{22} + 24 m^{14})$

5) 正二十面体：由表1知正十二面体的顶点数、边数及面数分别为12，30，20。图形结构如图5所示。我们给图形顶点标上数字标号，12个顶点如图依次记为 $1, 2, \dots, 12$ 。30条边依次记为： $e_{1} (1 2)$ ， $e_{2} (10 12)$ ， $e_{3} (1 3)$ ， $e_{4} (11 12)$ ， $e_{5} (2 3)$ ， $e_{6} (10 11)$ ， $e_{7} (1 4)$ ， $e_{8} (9 12)$ ， $e_{9} (2 4)$ ， $e_{10} (9 10)$ ， $e_{11} (1 8)$ ， $e_{12} (6 12)$ ， $e_{13} (4 8)$ ， $e_{14} (6 9)$ ， $e_{15} (1 5)$ ， $e_{16} (7 12)$ ， $e_{17} (5 8)$ ， $e_{18} (6 7)$ ， $e_{19} (3 5)$ ， $e_{20} (7 11)$ ， $e_{21} (5 9)$ ， $e_{22} (4 7)$ ， $e_{23} (5 10)$ ， $e_{24} (2 7)$ ， $e_{25} (8 11)$ ， $e_{26} (3 6)$ ， $e_{27} (3 9)$ ， $e_{28} (4 11)$ ， $e_{29} (8 10)$ ， $e_{30} (2 6)$ 。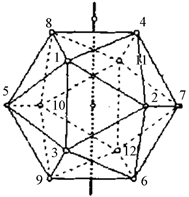20个面依次记为： $u_{1} (1 2 3)$ ， $u_{2} (10 11 12)$ ， $u_{3} (1 2 4)$ ， $u_{4} (9 10 12)$ ， $u_{5} (1 4 8)$ ， $u_{6} (6 9 12)$ ， $u_{7} (1 5 8)$ ， $u_{8} (6 7 12)$ ， $u_{9} (1 3 5)$ ， $u_{10} (7 11 12)$ ， $u_{11} (3 5 9)$ ， $u_{12} (4 7 11)$ ， $u_{13} (5 9 10)$ ， $u_{14} (2 4 7)$ ， $u_{15} (5 8 10)$ ， $u_{16} (2 6 7)$ ， $u_{17} (8 10 11)$ ， $u_{18} (2 3 6)$ ， $u_{19} (4 8 11)$ ， $u_{20} (3 6 9)$ 。

Figure 5. Regular dodecahedron body structure

图5. 正十二面体体结构图

正二十面体的轴旋转可分为三类：

I类为过对面中心的连线，旋转120˚和240˚，以通过面 $u_{5} (1 4 8)$ 和其对面 $u_{6} (6 9 12)$ 中心的连线旋转120˚为例，其点置换 $(1 4 8)$ $(12 9 6)$ $(5 2 11)$ $(7 10 3)$ 是3⁴型置换，求得对应的边置换为 $(e_{1} e_{17} e_{28})$ $(e_{2} e_{18} e_{27})$ $(e_{3} e_{29} e_{22})$ $(e_{4} e_{30} e_{21})$ $(e_{5} e_{23} e_{20})$ $(e_{6} e_{24} e_{19})$ $(e_{7} e_{11} e_{13})$ $(e_{8} e_{12} e_{14})$ $(e_{9} e_{15} e_{25})$ $(e_{10} e_{16} e_{26})$ 是3¹⁰型置换，对应的面置换为 $(u_{5})$ $(u_{6})$ $(u_{1} u_{12} u_{15})$ $(u_{2} u_{11} u_{16})$ $(u_{3} u_{19} u_{7})$ $(u_{4} u_{20} u_{8})$ $(u_{9} u_{14} u_{17})$ $(u_{10} u_{13} u_{18})$ 是1²3⁶型置换，有十组对面，两种转角，共20个元素；

II类为过对顶点连线为轴，旋转72˚、144˚、216˚和288˚，以(1 12)为对顶点的连线为轴顺时针旋转72˚为例，其点置换 $(1)$ $(12)$ $(2 3 5 8 4)$ $(7 6 9 10 11)$ 是1²5²型置换，诱导出对应的边置换为 $(e_{1} e_{3} e_{15} e_{11} e_{7})$ $(e_{5} e_{19} e_{17} e_{13} e_{9})$ $(e_{2} e_{4} e_{16} e_{12} e_{8})$ $(e_{6} e_{20} e_{18} e_{14} e_{10})$ $(e_{30} e_{27} e_{23} e_{25} e_{22})$ $(e_{26} e_{21} e_{29} e_{28} e_{24})$ 是5⁶型置换，对应的面置换为 $(u_{1} u_{9} u_{7} u_{5} u_{3})$ $(u_{2} u_{10} u_{8} u_{6} u_{4})$ $(u_{18} u_{11} u_{15} u_{19} u_{14})$ $(u_{20} u_{13} u_{17} u_{12} u_{10})$ 是5⁴型置换，有六组对顶点，四种转角，共24个元素；

III类为对边中点的连线为旋转轴，旋转180˚，以边 $e_{13} (4 8)$ 和其对边 $e_{14} (6 9)$ 中点连线为轴旋转180˚为例，其点置换 $(4 8)$ $(9 6)$ $(1 11)$ $(3 12)$ $(5 7)$ $(2 10)$ 是2⁶型置换，求得对应的边置换 $(e_{13})$ $(e_{14})$ $(e_{1} e_{6})$ $(e_{2} e_{5})$ $(e_{3} e_{4})$ $(e_{7} e_{25})$ $(e_{8} e_{26})$ $(e_{9} e_{29})$ $(e_{10} e_{30})$ $(e_{11} e_{28})$ $(e_{12} e_{27})$ $(e_{15} e_{20})$ $(e_{16} e_{19})$ $(e_{17} e_{22})$ $(e_{18} e_{21})$ $(e_{23} e_{24})$ 是1²2¹⁴型置换，求得对应的面置换为 $(u_{1} u_{2})$ $(u_{3} u_{17})$ $(u_{4} u_{18})$ $(u_{5} u_{19})$ $(u_{6} u_{20})$ $(u_{7} u_{12})$ $(u_{8} u_{11})$ $(u_{9} u_{10})$ $(u_{13} u_{16})$ $(u_{14} u_{15})$ 是2¹⁰型置换，有15组对边，一种转角，共15个元素。

加上单位元，点置换群有1¹²型1个，3⁴型20个，1²5²型24个，2⁶型15个；边置换群有1³⁰型1个，3¹⁰型20个，5⁶型24个，1²2¹⁴型15个；面置换群有1²⁰型1个，1²3⁶型20个，5⁴型24个，2¹⁰型15个；对每个类型置换计算不动点数，由Pólya定理即可得到正二十面体的m种颜色的顶点、边、面着色公式为：

$N_{V_{20}} = \frac{1}{60} (m^{12} + 15 m^{6} + 44 m^{4})$ , $N_{E_{20}} = \frac{1}{60} (m^{30} + 15 m^{16} + 20 m^{10} + 24 m^{6})$ ,

$N_{U_{20}} = \frac{1}{60} (m^{20} + 15 m^{10} + 20 m^{8} + 24 m^{4})$

由点、边、面的置换群类型及个数，可得出正二十面体的点边置换群 $V E_{20}$ 有1⁴²型1个，3¹⁴型20个，1²5⁸型24个，1²2²⁰型15个；点面置换群 $V U_{20}$ 有1³²型1个，1²3¹⁰型20个，1²5⁶型24个，1²5⁶型20个，2¹⁶型15个；边面置换群 $E U_{20}$ 有1⁵⁰型1个，1²3¹⁶型20个，5¹⁰型24个，1²2²⁴型15个；点边面置换群 $V E U_{20}$ 有1⁶²型1个，1²5¹²型24个，1²3²⁰型20个，1²2³⁰型15个；由Pólya定理即可得到正二十面体的m种颜色的点边、点面、边面和点边面着色公式分别为：

$N_{V E_{20}} = \frac{1}{60} (m^{42} + 15 m^{22} + 20 m^{14} + 24 m^{10})$ , $N_{V U_{20}} = \frac{1}{60} (m^{32} + 15 m^{16} + 20 m^{12} + 24 m^{8})$

$N_{E U_{20}} = \frac{1}{60} (m^{50} + 15 m^{26} + 20 m^{18} + 24 m^{10})$ , $N_{V E U_{20}} = \frac{1}{60} (m^{62} + 15 m^{32} + 20 m^{22} + 24 m^{14})$

参考文献

[1]	胡冠章. 应用近世代数[M]. 北京: 清华大学出版社, 1999.
[2]	叶载良, 韩冬. 正多面体的顶点着色公式[J]. 商洛师范专科学校学报, 2005, 19(3): 89-93.
[3]	Dixon, J.D. and Mortimer, B. (1996) Permutation Groups. Graduate Texts in Mathematics. Springer-Verlag, Berlin.
[4]	曹汝成. 组合数学[M]. 广州: 华南理工大学出版社, 2000.
[5]	丘维声. 抽象代数基础[M]. 北京: 高等教育出版社, 2003.
[6]	徐俊明. 图论及应用[M]. 合肥: 中国科学技术大学出版社, 1998.

为你推荐

友情链接