具有某类L^δ-(logL)^ρ核函数的Marcinkiewicz积分交换子的双权估计

Double Weighted Estimates for the Commutator of Marcinkiewicz Integral with Some L^δ-(logL)^ρ Kernel

摘要: 本文证明核函数满足L^δ-(logL)^ρ条件的Marcinkiewicz积分μ_Ω与加权Lipschitz函数b生成的交换子μ_Ω，b具有(H^p(ω),L^q(ω^1-q))和(H^n/n+β(ω),L^1,∞)有界性。

Abstract: In this paper, we obtain that the commutator μ_Ω，b generated by Marcinkiewicz integral μ_Ω with L^δ-(logL)^ρ kernel and weighted Lipschitz function b, has (H^p(ω),L^q(ω^1-q)) and (H^n/n+β(ω),L^1,∞) boundedness.

1. 引言

设 $S^{n-1}$ 是 $R^n$ 上的单位球面且具有标准的Lebesgue测度， $\Omega \in L^{\infty }\left(S^{n-1}\right)$ 是 $S^{n-1}$ 上的零次齐次函数且满

足：对任意的 $x\ne 0,x^{\prime }=\frac{x}{\left|x\right|}$，

${\displaystyle {\int }_{S^{n-1}}\Omega }\left(x^{\prime }\right)\text{d}\sigma \left(x^{\prime }\right)=0.$ (1.1)

定义Marcinkiewicz积分算子为

${\mu }_{\Omega }\left(f\right)\left(x\right)={\left({\displaystyle {\int }_0^{\infty }{\left|{\displaystyle {\int }_{\left|x-y\right|\le t}\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}}f\left(y\right)\text{d}y\right|}^2\frac{\text{d}t}{t^3}}\right)}^{\frac{1}{2}}.$

由Marcinkiewicz积分 ${\mu }_{\Omega }$ 和适当的函数b生成的交换子定义为

${\mu }_{\Omega ,b}\left(f\right)\left(x\right)={\left({\displaystyle {\int }_0^{\infty }{\left|{\displaystyle {\int }_{\left|x-y\right|\le t}\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}}\left[b\left(x\right)-b\left(y\right)\right]f\left(y\right)\text{d}y\right|}^2\frac{\text{d}t}{t^3}}\right)}^{\frac{1}{2}}.$

如果存在常数 $C>0$ 和 $\rho >1$，使得对任意的 $y_1,y_2\in S^{n-1}$，有

$\left|\Omega \left(y_1\right)-\Omega \left(y_2\right)\right|\le \frac{C}{{\left(\log \frac{2}{\left|y_1-y_2\right|}\right)}^{\rho }},$ (1.2)

则称 $\Omega$ 满足log型Lipschitz条件。

Marcinkiewicz首先在文 [1] 中给出了一维Marcinkiwicz算子 ${\mu }_{\Omega }$ 的定义，此时 $\Omega \left(t\right)=\text{sign}\left(t\right)$。1958年，Stein在 [2] 中定义了高维的Marcinkiewicz积分，并证明当 $\Omega \in Li{p}_{\alpha }\left(S^{n-1}\right),0<\alpha \le 1$ 时， ${\mu }_{\Omega }$ 是强 $\left(p,p\right)\left(1<p\le 2\right)$ 型和弱 $\left(1,1\right)$ 型的。2004年，Lee和Rim在 [3] 中引入log型Lipschitz条件(1.2)，并证明当 $\Omega$ 满足(1.2)时Marcinkiewicz积分 ${\mu }_{\Omega }$ 的 $\left(H^1,L^1\right),\left(L^{\infty },BMO\right)$ 和 $\left(L^p,L^p\right)\left(1<p<\infty \right)$ 有界性。显然条件(1.2)比Stein定理中的Lipschitz条件更弱。关于Marcinkiewicz积分算子有界性的结果很多，范大山、陈杰诚、丁勇、陆善镇和Yabuta等人在这一领域做出了巨大贡献，文献较多就不一一枚举。

对于Marcinkiewicz积分交换子，Torchinsky和Wang在 [4] 中证明当核函数满足Lipschitz条件时Marcinkiewicz积分和它的交换子在加权 $L^p\left(1<p<\infty \right)$ 上有界，Ding、Lu和Yabuta在 [5] 中讨论带粗糙核的Marcinkiewicz积分与BMO函数生成的高阶交换子的加权有界性。Ding、Lu和Zhang [6] 建立了Marcinkiewicz积分交换子的 $\left(L\log L,L^{1,\infty }\right)$ 有界性。2008年，王、张和刘 [7] 给出核函数满足条件(1.2)时，Marcinkiewicz积分交换子在Hardy空间上的端点估计。Lin、Liu和Wang [8] 将 [7] 的结果推广到加权情形。另一方面，陆、吴和杨 [9] 研究了奇异积分算子和Lipschitz函数生成的交换子在Hardy空间上的端点估计。

如果存在常数 $C>0\text{,}\delta >0$ 和 $\rho >1$，使得对任意的 $y_1,y_2\in S^{n-1}$，有

$\left|\Omega \left(y_1\right)-\Omega \left(y_2\right)\right|\le \frac{C{\left|y_1-y_2\right|}^{\delta }}{{\left(\log \frac{2}{\left|y_1-y_2\right|}\right)}^{\rho }},$ (1.3)

则称 $\Omega \left(x\right)$ 满足 $L^{\delta }-{\left(\log L\right)}^{\rho }$ 条件。条件(1.3)比log型Lipschitz条件(1.2)弱。当 $\delta =0$ 时， $L^{\delta }-{\left(\log L\right)}^{\rho }$ 条件即为log型Lipschitz条件。Wang在文 [10] 中讨论变量核的参数型Marcinkiewicz积分算子 ${\mu }_{\Omega }^{\varrho }$，得到核函数满足消失性条件和 $L^{\delta }-{\left(\log L\right)}^{\rho }$ 条件时， ${\mu }_{\Omega }^{\varrho }$ 在Hardy空间 $H^p\left(R^n\right)$ 和弱Hardy空间 $W{H}^p\left(R^n\right)$ 上的有界性。

受文献 [7] [8] 和 [9] 的启发，我们将研究核函数满足 $L^{\delta }-{\left(\log L\right)}^{\rho }$ 条件(1.3)时，Marcinkiewicz积分算子和加权Lipschitz函数生成的交换子在加权Hardy空间上的有界性。具体地，即建立Marcinkiewicz积分

交换子 ${\mu }_{\Omega ,b}$ 的 $\left(H^p\left(\omega \right),L^q\left({\omega }^{1-q}\right)\right)$ 和 $\left(H^{\frac{n}{n+\beta }}\left(\omega \right),L^{1,\infty }\right)$ 有界性。为此，首先给出本文的一些基本定义。

定义1.1 设 $\omega$ 为一个权函数， $1\le p<\infty$。若一个局部可积函数 $b\left(x\right)$ 满足

$\underset{B}{\text{sup}}\frac{1}{\omega {\left(B\right)}^{\beta /n}}{\left(\frac{1}{\omega \left(B\right)}{\displaystyle {\int }_B{\left|b\left(x\right)-b_B\right|}^p\omega {\left(x\right)}^{1-p}\text{d}x}\right)}^{1/p}\le C<\infty ,$

其中上确界取遍所有的球 $B\subset {\text{R}}^n,\omega \left(B\right)={\displaystyle {\int }_B\omega }\left(x\right)\text{d}x$。则称b属于加权Lipschitz空间，记为 $b\in Li{p}_{\beta ,\omega }^p$。上式中C的最小下确界称为b的 $Li{p}_{\beta ,\omega }^p$ 范数，记为 ${\Vert b\Vert }_{Li{p}_{\beta ,\omega }^p}$。对不同的 $p_1$ 和 $p_2$，函数b的 ${\Vert b\Vert }_{Li{p}_{\beta ,\omega }^{p_1}}$ 和 ${\Vert b\Vert }_{Li{p}_{\beta ,\omega }^{p_2}}$ 等价，因此通常可以记b的加权Lipschitz范数为 ${\Vert b\Vert }_{Li{p}_{\beta ,\omega }}$，见文献 [11]。

本文结果如下。

定理1.1 设 $\omega \in A_1\left(R^n\right),b\in Li{p}_{\beta ,\omega },0<\beta <\frac{1}{2}$ 以及 $\Omega$ 满足光滑性条件(1.3)。若 $\frac{n}{n+1}<p\le 1$ 且 $\frac{1}{q}=\frac{1}{p}-\frac{\beta }{n}$。

则 ${\mu }_{\Omega ,b}$ 是 $H^p\left(\omega \right)$ 到 $L^q\left({\omega }^{1-q}\right)$ 上的有界算子。

定理1.2 设 $\omega \in A_1\left(R^n\right),b\in Li{p}_{\beta ,\omega },0<\beta <\frac{1}{2}$ 以及 $\Omega$ 满足光滑性条件(1.3)且 $\delta \ge \beta$。则交换子 ${\mu }_{\Omega ,b}$ 是 $H^{\frac{n}{n+\beta }}\left(\omega \right)$ 到 $L^{1,\infty }$ 有界的。即对任意的 $\lambda >0$，存在常数 $C>0$，使得

$\left|\left\{x\in R^n:\left|{\mu }_{\Omega }\left(f\right)\left(x\right)\right|>\lambda \right\}\right|\le C{\lambda }^{-1}{\Vert f\Vert }_{H^{\frac{n}{n+\beta }}\left(\omega \right)}.$

2. 预备知识和相关引理

这节介绍一些我们所需的概念和引理。先给出 $A_p$ 权的定义。

定义2.1 设 $1<p<\infty$。如果对任意 $B\subset {\text{R}}^n$，存在常数 $C>0$ 使得

$\left(\frac{1}{\left|B\right|}{\displaystyle {\int }_B\omega }\left(x\right)\text{d}x\right){\left(\frac{1}{\left|B\right|}{\displaystyle {\int }_B\omega }{\left(x\right)}^{-\frac{1}{p-1}}\text{d}x\right)}^{p-1}\le C<\infty ,$

则称权函数 $\omega \in A_p$。如果存在常数 $C>0$，使得 $\frac{1}{\left|B\right|}{\displaystyle {\int }_B\omega }\left(x\right)\text{d}x\le C\omega \left(x\right),a.ex\in {\text{R}}^n$，则称权函数 $\omega \in A_1$。

下面介绍加权Hardy空间的概念及原子分解。

定义2.2 记S为Schwartz函数类， $S^{\prime }$ 是它的对偶。设 $\phi \in S,{\displaystyle \int \phi }=1$， $\omega$ 为权函数。定义的极

大函数 $M_{\phi }f\left(x\right)=\underset{t>0}{\text{sup}}\left|{\phi }_t\ast f\left(x\right)\right|$。加权Hardy空间定义为 $H^p\left(\omega \right)=\left\{f\in S^{\prime }\left(R^n\right):M_{\phi }f\in L^p\left(\omega \right)\right\}$ 且记 ${\Vert f\Vert }_{H^p\left(\omega \right)}={\Vert M_{\phi }f\Vert }_{L^p\left(\omega \right)}$。

定义2.3 设 $\omega$ 是一个权函数， $\frac{n}{n+1}<p\le 1$。a是一个有界的可测函数，如果它满足下面的条件

(i) 存在一个球B使得；

(ii) ${\left|a\right|}_{\infty }\le \omega {\left(B\right)}^{-1/p}$ ；

(iii) ${\displaystyle \int a}\left(x\right)\text{d}x=0$，

则称a为加权的p-原子，球B为原子a的支集球。设f为缓增广义函数。如果在分布意义下f可以写成

$f={\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j}{a}_j$，这里 $a_j$ 是p-原子，N为任意的整数， ${\lambda }_j\in C$ 且 ${\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\left|{\lambda }_j\right|}^p}<\infty$，则称f属于原子加权Hardy

空间 $H^p\left(\omega \right)$，并定义 $H^p\left(\omega \right)$ 中的半范为

${\Vert f\Vert }_{H^p\left(\omega \right)}={\text{inf}}_{{\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j}{a}_j=f}{\left({\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\left|{\lambda }_j\right|}^p}\right)}^{1/p},$

其中下确界“inf”是对f的一切分解取的。

引理2.1 [12] 设 $\omega \in A_1$，则对于球B的任意可测子集E，存在常数 $C_1,C_2>0$ 和 $0<\delta <1$，使得

$C_1\frac{\left|E\right|}{\left|B\right|}\le \frac{\omega \left(E\right)}{\omega \left(B\right)}\le C_2{\left(\frac{\left|E\right|}{\left|B\right|}\right)}^{\delta }$

成立。如果 $\omega \left(x\right)$ 是常值函数，则 $\delta =1$ ；如果 $\omega \left(x\right)$ 不是常值函数，则 $0<\delta <1$。

引理2.2 [5] 设 $\Omega \in L^q\left(S^{n-1}\right)\left(q>1\right)$ 是一个零次齐次函数且满足条件(1.1)。若 $p,q$ 和 $\omega$ 满足下列条件之一：

(i) $q^{\prime }<p<\infty$ 和 $\omega \in A_{p/q^{\prime }}$ ；

(ii) $1<p<q$ 和 ${\omega }^{1-p^{\prime }}\in A_{p/q^{\prime }}$ ；

(iii) $1<p<\infty$ 和 ${\omega }^{q^{\prime }}\in A_p$，

则 ${\mu }_{\Omega }$ 在 $L_{\omega }^p$ 上有界。

引理2.3 [13] 设 $\omega \in A_1,b\in Li{p}_{\beta ,\omega }$，则

${\left({\displaystyle {\int }_{2^{k+1}B}{\left|b\left(y\right)-b_B\right|}^s\omega {\left(y\right)}^{1-s}\text{d}y}\right)}^{1/s}\le Ck{2}^{\left(k+1\right)\left(\beta +\frac{n}{s}\right)}\omega {\left(B\right)}^{\frac{\beta }{n}+\frac{1}{s}}{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}.$

引理2.4 设 $\omega \in A_1,b\in Li{p}_{\beta ,\omega }$，则

${\displaystyle {\int }_{2^{k+1}B}\left|b\left(y\right)-b_B\right|\text{d}y}\le Ck{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}{2}^{\left(k+1\right)\left(\beta +n\right)}\omega {\left(B\right)}^{\frac{\beta }{n}+1}.$

证明 利用Hölder不等式，引理2.3和引理2.1可得

$\begin{array}{c}{\displaystyle {\int }_{2^{k+1}B}\left|b\left(x\right)-b_B\right|\text{d}x}\\ \le {\left({\displaystyle {\int }_{2^{k+1}B}{\left|b\left(x\right)-b_B\right|}^2\omega {\left(x\right)}^{-1}\text{d}x}\right)}^{\frac{1}{2}}{\left({\displaystyle {\int }_{2^{k+1}B}\omega \left(x\right)\text{d}x}\right)}^{\frac{1}{2}}\\ \le k{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}{2}^{\left(k+1\right)\left(\beta +\frac{n}{2}\right)}\omega {\left(B\right)}^{\frac{\beta }{n}+\frac{1}{2}}\omega {\left(2^{k+1}B\right)}^{\frac{1}{2}}\\ \le Ck{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}{2}^{\left(k+1\right)\left(\beta +\frac{n}{2}\right)}\omega {\left(B\right)}^{\frac{\beta }{n}+\frac{1}{2}}{2}^{\left(k+1\right)\frac{n}{2}}\omega {\left(B\right)}^{\frac{1}{2}}\\ \le Ck{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}{2}^{\left(k+1\right)\left(\beta +n\right)}\omega {\left(B\right)}^{\frac{\beta }{n}+1}.\end{array}$

引理2.5 [14] 设 $\omega \in A_1\left(R^n\right),b\in Li{p}_{\beta ,\omega },0<\beta <1$。设 $1<r<\frac{n}{\beta }$ 且 $\frac{1}{r}=\frac{1}{p}-\frac{\beta }{n}$，则 ${\mu }_{\Omega ,b}$ 是到 $L^q\left({\omega }^{1-q}\right)$ 上的有界算子。

3. Marcinkiewicz积分交换子在加权Hardy空间上的有界性

下面给出Marcinkiewicz积分交换子的 $\left(H^p\left(\omega \right),L^q\left({\omega }^{-q}\right)\right)$ 和 $\left(H^{\frac{n}{n+\beta }}\left(\omega \right),L^{1,\infty }\right)$ 有界性证明。

定理1.1的证明 由于 ${\mu }_{\Omega ,b}$ 是次线性算子，所以只需要证明对每一个加权p-原子 $a_j$，有不等式

${\left|{\mu }_{\Omega ,b}\left(a_j\right)\right|}_{L^q\left({\omega }^{1-q}\right)}\le C.$ (3.1)

若(3.1)成立，由于 $\frac{n\left(n+\beta \right)}{n^2+n\beta +{\beta }^2}<p\le 1,q>1$，则对f的任意分解 $f={\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j}{a}_j\in H^p\left(\omega \right)$，利用定义2.3 (ii)

可得

$\begin{array}{c}{\Vert {\mu }_{\Omega ,b}\left(f\right)\Vert }_{L^q\left({\omega }^{1-q}\right)}\le {\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\Vert {\mu }_{\Omega ,b}\left(a_j\right)\Vert }_{L^q\left({\omega }^{1-q}\right)}}\le C{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|}\\ \le C{\left({\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\left|{\lambda }_j\right|}^p}\right)}^{\frac{1}{p}}\le C{\Vert f\Vert }_{H^p\left(\omega \right)}.\end{array}$

下面证明(3.1)。设 $\text{supp}{a}_j\subset B=B\left(x_0,r\right)$，则

$\begin{array}{l}{\Vert {\mu }_{\Omega ,b}\left(a_j\right)\Vert }_{L^q\left({\omega }^{1-q}\right)}\\ \le {\left({\displaystyle {\int }_{2B}{\left|{\mu }_{\Omega ,b}\left(a_j\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\right)}^{1/q}+{\left({\displaystyle {\int }_{{\left(2B\right)}^c}{\left|{\mu }_{\Omega ,b}\left(a_j\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\right)}^{1/q}\\ :=I_1+I_2.\end{array}$

取 $p_1>1,1<q<q_1<\infty$ 且 $\frac{1}{q_1}=\frac{1}{p_1}-\frac{\beta }{n}$。利用Hölder不等式，引理2.5和定义2.3 (ii)可得

$\begin{array}{l}{I}_1={\left({\displaystyle {\int }_{2B}{\left|{\mu }_{\Omega ,b}\left(a_j\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\right)}^{1/q}\\ \le {\left({\displaystyle {\int }_{2B}{\left|{\mu }_{\Omega ,b}\left(a_j\right)\right|}^{q_1}\omega {\left(x\right)}^{1-q_1}\text{d}x}\right)}^{1/q}{\left({\displaystyle {\int }_{2B}\omega }\left(x\right)\text{d}x\right)}^{\frac{1}{q}-\frac{1}{q_1}}\\ \le C{\Vert a_j\Vert }_{L^{p_1}\left(\omega \right)}\omega {\left(B\right)}^{\frac{1}{q}-\frac{1}{q_1}}\le C{\Vert a_j\Vert }_{\infty }\omega {\left(B\right)}^{\frac{1}{p_1}}\omega {\left(B\right)}^{\frac{1}{q}-\frac{1}{q_1}}\\ \le C\omega {\left(B\right)}^{-\frac{1}{p}}\omega {\left(B\right)}^{\frac{1}{p_1}}\omega {\left(B\right)}^{\frac{1}{q}-\frac{1}{q_1}}\le C.\end{array}$

对于 $I_2$，有

$\begin{array}{l}{I}_2={\left({\displaystyle {\int }_{{\left(2B\right)}^c}{\left|\left[b,{\mu }_{\Omega }\left(a_j\right)\right]\left(x\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\right)}^{1/q}\\ \le {\left({\displaystyle {\int }_{{\left(2B\right)}^c}{\left|\left(b\left(x\right)-b_B\right){\mu }_{\Omega }\left(a_j\right)\left(x\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\right)}^{1/q}\\ +{\left({\displaystyle {\int }_{{\left(2B\right)}^c}{\left|{\mu }_{\Omega }\left(\left(b-b_B\right)a_j\right)\left(x\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\right)}^{1/q}\\ :={\left(I{I}_1\right)}^{\frac{1}{q}}+{\left(I{I}_2\right)}^{\frac{1}{q}}.\end{array}$

而对于 $I{I}_{\text{1}}$，有

$\begin{array}{l}I{I}_1\le {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}{\left({\displaystyle {\int }_0^{\infty }{\left|F_{\Omega ,t}\left(a_j\right)\left(x\right)\right|}^2\frac{\text{d}t}{t^3}}\right)}^{\frac{q}{2}}\omega {\left(x\right)}^{1-q}\text{d}x}\\ ={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}}{\left({\displaystyle {\int }_0^{\left|x-x_0\right|+2r}{\left|F_{\Omega ,t}\left(a_j\right)\left(x\right)\right|}^2\frac{\text{d}t}{t^3}}\right)}^{\frac{q}{2}}\omega {\left(x\right)}^{1-q}\text{d}x\\ +\sum {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}{\left({\displaystyle {\int }_{\left|x-x_0\right|+2r}^{\infty }{\left|F_{\Omega ,t}\left(a_j\right)\left(x\right)\right|}^2\frac{\text{d}t}{t^3}}\right)}^{\frac{q}{2}}\omega {\left(x\right)}^{1-q}\text{d}x}\\ :=I{I}_{11}+I{I}_{12}.\end{array}$

接下来首先估计 $I{I}_{11}$。当 $x\in B,y\in R^n\backslash \tilde{B}$ 时有 $\left|x-y\right|\sim \left|x_0-y\right|\sim \left|x_0-y\right|+2r$，因此有

$\left|\frac{1}{{\left|x-y\right|}^2}-\frac{1}{{\left(\left|x_0-y\right|+2r\right)}^2}\right|\le \frac{Cr}{{\left|x-y\right|}^3},\left|\frac{x-y}{\left|x-y\right|}-\frac{x-x_0}{\left|x-x_0\right|}\right|\le \frac{Cr}{\left|x-x_0\right|},$ (3.2)

且

$\begin{array}{c}\left|\Omega \left(x-y\right)-\Omega \left(x-x_0\right)\right|=\left|\Omega \left(\frac{x-y}{\left|x-y\right|}\right)-\Omega \left(\frac{x-x_0}{\left|x-x_0\right|}\right)\right|\\ \le {\left(\frac{r}{\left|x-x_0\right|}\right)}^{\delta }\frac{C}{{\left(\log \frac{\left|x-x_0\right|}{r}\right)}^{\rho }}.\end{array}$ (3.3)

因此有

$\begin{array}{l}\left|\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}-\frac{\Omega \left(x_0-y\right)}{{\left|x_0-y\right|}^{n-1}}\right|\\ \le \frac{\left|\Omega \left(x-y\right)-\Omega \left(x_0-y\right)\right|}{{\left|x_0-y\right|}^{n-1}}+\left|\Omega \left(x-y\right)\right|\left|\frac{1}{{\left|x-y\right|}^{n-1}}-\frac{1}{{\left|x_0-y\right|}^{n-1}}\right|\\ \le \frac{C{\left(\frac{r}{\left|x-x_0\right|}\right)}^{\delta }}{{\left|x_0-y\right|}^{n-1}{\left(\log \frac{\left|x-x_0\right|}{r}\right)}^{\rho }}+\frac{r}{{\left|x_0-y\right|}^n}\le \frac{C{\left(\frac{r}{\left|x-x_0\right|}\right)}^{\delta }}{{\left|x_0-y\right|}^{n-1}{\left(\log \frac{\left|x_0-y\right|}{r}\right)}^{\rho }}.\end{array}$ (3.4)

利用Minkowski不等式，(3.2)式，零次其次函数 $\Omega \in L^{\infty }\left(S^{n-1}\right)$ 和引理2.3可得

$\begin{array}{c}I{I}_{11}\le {{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}\left({\displaystyle {\int }_{R^n}\frac{\left|\Omega \left(x-y\right)\right|\left|a_j\right|}{{\left|x-y\right|}^{n-1}}}{\left({\displaystyle {\int }_{\left|x-y\right|\le t\le \left|x_0-y\right|+2r}\frac{\text{d}t}{t^3}}\right)}^{\frac{1}{2}}\text{d}y\right)}}^q\omega {\left(x\right)}^{1-q}\text{d}x\\ \le {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}{\left({\displaystyle {\int }_B\frac{\left|\Omega \left(x-y\right)\right|\left|a_j\right|}{{\left|x-y\right|}^{n-1}}}\frac{C{r}^{\frac{1}{2}}}{{\left|x-y\right|}^{\frac{3}{2}}}\text{d}y\right)}^q\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le C{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}{\Vert a_j\Vert }_{\infty }{2}^{-k\left(n+\frac{1}{2}\right)q}\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le C{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\omega {\left(B\right)}^{-\frac{q}{p}}{2}^{-k\left(n+\frac{1}{2}\right)q}{\displaystyle {\int }_{2^{k+1}B}{\left|b\left(x\right)-b_B\right|}^q}\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le C{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\omega {\left(B\right)}^{-\frac{q}{p}}{2}^{-k\left(n+\frac{1}{2}\right)q}k\omega {\left(B\right)}^{\frac{q\beta }{n}+1}{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}^q{2}^{\left(k+1\right)\left(n+q\beta \right)}}\\ \le C{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}k{2}^{-kn\left(q-1\right)}{2}^{-kq\left(\frac{1}{2}-\beta \right)}}\le C.\end{array}$

接着估计 $I{I}_{12}$。利用原子 $a_j$ 的消失性，Minkowski不等式，(3.4)和引理2.3可得

$\begin{array}{l}I{I}_{12}\le {\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}{\left({\displaystyle {\int }_{R^n}\left|\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}-\frac{\Omega \left(x-x_0\right)}{{\left|x-x_0\right|}^{n-1}}\right|\left|a_j\right|}{\left({\displaystyle {\int }_{\left|x_0-y\right|+2r}^{\infty }\frac{\text{d}t}{t^3}}\right)}^{\frac{1}{2}}\text{d}y\right)}^q\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le C{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}{\left|b\left(x\right)-b_B\right|}^q}{\left({\displaystyle {\int }_B\frac{\left|a_j\left(y\right)\right|{\left(\frac{r}{\left|x-x_0\right|}\right)}^{\delta }}{{\left|x-x_0\right|}^{n-1}{\left(\log \frac{\left|x-y\right|}{r}\right)}^{\rho }}}\frac{1}{\left|x-x_0\right|}\text{d}y\right)}^q\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le C{r}^{\delta }{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\omega {\left(B\right)}^{-\frac{q}{p}}{2}^{-k\left(n+\delta \right)q}{\left(\log 2^k\right)}^{-\rho q}{\displaystyle {\int }_{2^{k+1}B}{\left|b\left(x\right)-b_B\right|}^q}\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le C{r}^{\delta }{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\omega {\left(B\right)}^{-\frac{q}{p}}{2}^{-k\left(n+\delta \right)q}{k}^{-\rho q}k\omega {\left(B\right)}^{\frac{q\beta }{n}+1}{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}^q{2}^{\left(k+1\right)\left(n+q\beta \right)}}\\ \le C{r}^{\delta }{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{k}^{1-\rho q}{2}^{-kn\left(q-1\right)}{2}^{-kq\left(\delta -\beta \right)}}\le C,\end{array}$

这里最后一个不等式用到 $q>1$ 和 $\delta >\beta$，从而级数收敛。最后估计 $I{I}_2$。利用引理2.2 (i)，定义1.2，定义

2.3 (ii)以及 $\frac{1}{q}=\frac{1}{p}-\frac{\beta }{n}$ 可得

$\begin{array}{l}I{I}_2\le {\displaystyle {\int }_{R^n}{\left|{\mu }_{\Omega }\left(\left(b-b_B\right)a_j\right)\left(x\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le {\displaystyle {\int }_B{\left|b-b_B\right|}^q{\left|a_j\left(x\right)\right|}^q\omega {\left(x\right)}^{1-q}\text{d}x}\\ \le \omega {\left(B\right)}^{-\frac{q}{p}}\omega {\left(B\right)}^{\frac{q\beta }{n}+1}{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}^q\le C.\end{array}$

结合 $I_1,I_2$ 的估计可得(3.1)。定理证毕。

定理1.3的证明 记 $f={\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j}{a}_j$，其中a_j是 $\omega -\left(\frac{n}{n+\beta },\infty \right)$ 原子且满足 ${\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j}<\infty ,\text{supp}{a}_j\subset B=B\left(x_0,r\right)$。则

$\begin{array}{l}\left|{\mu }_{\Omega ,b}f\left(x\right)\right|\\ =\left|\left[b,{\mu }_{\Omega }\left({\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j}{a}_j\right)\right]\left(x\right)\right|\\ \le \left|{\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j\left(b\left(x\right)-b_B\right){\mu }_{\Omega }\left(a_j\right)\left(x\right){\chi }_{4B}\left(x\right)}\right|\\ +\left|{\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j\left(b\left(x\right)-b_B\right){\mu }_{\Omega }\left(a_j\right)}\left(x\right){\chi }_{{\left(4B\right)}^c}\left(x\right)\right|\\ +\left|{\mu }_{\Omega }\left({\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j\left(b-b_B\right)a_j}\right)\left(x\right)\right|\\ :=J_1+J_2+J_3.\end{array}$

利用Hölder不等式，引理2.2 (i)，定义1.1， $a_j$ 是 $\omega -\left(\frac{n}{n+\beta },\infty \right)$ 原子和引理2.3可得

$\begin{array}{l}{\Vert J_1\Vert }_{L^1}\\ \le C{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\left({\displaystyle {\int }_{4B}{\left|b\left(x\right)-b_B\right|}^2\omega {\left(x\right)}^{-1}\text{d}x}\right)}^{1/2}{\left({\displaystyle {\int }_{4B}{\left|{\mu }_{\Omega }\left(a_j\right)\left(x\right)\right|}^2\omega \left(x\right)\text{d}x}\right)}^{1/2}}\\ \le C{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\left({\displaystyle {\int }_{4B}{\left|b\left(x\right)-b_B\right|}^2\omega {\left(x\right)}^{-1}\text{d}x}\right)}^{1/2}{\left({\displaystyle {\int }_{4B}{\left|a_j\left(x\right)\right|}^2\omega \left(x\right)\text{d}x}\right)}^{1/2}}\\ \le C{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|2^{2\left(\beta +\frac{n}{2}\right)}\omega {\left(B\right)}^{\frac{\beta }{n}+\frac{1}{2}}{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}\omega {\left(B\right)}^{-\frac{n+\beta }{n}}\omega {\left(B\right)}^{\frac{1}{2}}}\\ \le C{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|}.\end{array}$

对于 $J_2$，有

$\begin{array}{l}{\Vert J_2\Vert }_{L^1}\le {\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\Vert \left(b\left(x\right)-b_B\right){\mu }_{\Omega }\left(a_j\right)\left(x\right){\chi }_{{\left(4B\right)}^c}\left(x\right)\Vert }_{L^1}}\\ \le {\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\displaystyle {\int }_{R^n\setminus 4B}\left|b\left(x\right)-b_B\right|}{\left({\displaystyle {\int }_0^{\infty }{\left|{\displaystyle {\int }_{\left|x-y\right|\le t}\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}{a}_j\left(y\right)\text{d}y}\right|}^2\frac{\text{d}t}{t^3}}\right)}^{1/2}\text{d}x}\\ \le {\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\displaystyle {\int }_{R^n\setminus 4B}\left|b\left(x\right)-b_B\right|}{\left({\displaystyle {\int }_0^{\left|x-x_0\right|+4r}{\left|{\displaystyle {\int }_{\left|x-y\right|\le t}\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}{a}_j\left(y\right)\text{d}y}\right|}^2\frac{\text{d}t}{t^3}}\right)}^{1/2}\text{d}x}\\ +{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\displaystyle {\int }_{R^n\setminus 4B}\left|b\left(x\right)-b_B\right|}{\left({\displaystyle {\int }_{\left|x-x_0\right|+4r}^{\infty }{\left|{\displaystyle {\int }_{\left|x-y\right|\le t}}\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}{a}_j\left(y\right)\text{d}y\right|}^2\frac{\text{d}t}{t^3}}\right)}^{1/2}\text{d}x}\\ :={\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|}\left(K_1+K_2\right).\end{array}$

接下来我们分别估计 $K_1$ 和 $K_2$。首先对于 $K_1$，我们利用Minkowski不等式，(3.2)式，定义2.3 (ii)和引理2.4可得

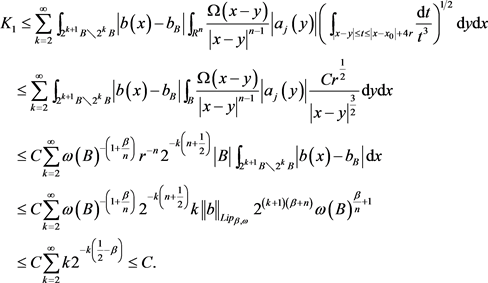
接着估计 $K_2$，利用原子 $a_j$ 的消失性，Minkowski不等式，(3.4)和引理2.3可得

$\begin{array}{l}{K}_2\le {\displaystyle \underset{k=2}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}\left|b\left(x\right)-b_B\right|}{\displaystyle {\int }_{R^n}\left|\frac{\Omega \left(x-y\right)}{{\left|x-y\right|}^{n-1}}-\frac{\Omega \left(x-x_0\right)}{{\left|x-x_0\right|}^{n-1}}\right|}\left|a_j\left(y\right)\right|{\left({\displaystyle {\int }_{\left|x-x_0\right|+4r}^{\infty }\frac{\text{d}t}{t^3}}\right)}^{1/2}\text{d}y\text{d}x}\\ \le {\displaystyle \underset{k=2}{\overset{\infty }{\sum }}{\displaystyle {\int }_{2^{k+1}B\setminus 2^{k}B}\left|b\left(x\right)-b_B\right|}{\displaystyle {\int }_B\frac{\left|a_j\left(y\right)\right|{\left(\frac{r}{\left|x-x_0\right|}\right)}^{\delta }}{{\left|x-x_0\right|}^{n-1}{\left(\log \frac{\left|x-x_0\right|}{r}\right)}^{\rho }}}\frac{1}{\left|x-x_0\right|}\text{d}y\text{d}x}\\ \le C{\displaystyle \underset{k=2}{\overset{\infty }{\sum }}{\left(2^{k}r\right)}^{-n}{2}^{-k\delta }{r}^{\delta }{\left(\log 2^k\right)}^{-\rho }\omega {(B)}^{-\left(1+\frac{\beta }{n}\right)}\left|B\right|{\displaystyle {\int }_{2^{k+1}B}\left|b\left(x\right)-b_B\right|\text{d}x}}\\ \le C{r}^{\delta }{\displaystyle \underset{k=2}{\overset{\infty }{\sum }}{2}^{-kn}{2}^{-k\delta }{k}^{-\rho }\omega {\left(B\right)}^{-\left(1+\frac{\beta }{n}\right)}k{\Vert b\Vert }_{Lip,\beta }\omega {\left(B\right)}^{-\left(1+\frac{\beta }{n}\right)}{2}^{\left(k+1\right)\left(n+\beta \right)}}\\ \le C{r}^{\delta }{\displaystyle \underset{k=2}{\overset{\infty }{\sum }}{k}^{1-\rho }{2}^{-k\left(\delta -\beta \right)}}\le C,\end{array}$

其中最后一个不等式利用了 $\delta >\beta$ 从而级数收敛。因此

${\Vert J_2\Vert }_{L^1}\le C{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|}.$

最后，利用引理2.7，定义2.1和定义2.3 (ii)，有

$\begin{array}{c}\left|\left\{x\in R^n:\left|J_3\right|>\frac{\lambda }{3}\right\}\right|\le C{\lambda }^{-1}{\Vert {\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\lambda }_j}\left(b-b_B\right)a_j\left(x\right)\Vert }_{L^1}\\ \le C{\lambda }^{-1}\omega {\left(B\right)}^{-\left(1+\frac{\beta }{n}\right)}{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|{\displaystyle {\int }_B\left|b\left(x\right)-b_B\right|\text{d}x}}\\ \le C{\lambda }^{-1}\omega {\left(B\right)}^{-\left(1+\frac{\beta }{n}\right)}{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|\omega {\left(B\right)}^{1+\frac{\beta }{n}}{\Vert b\Vert }_{Li{p}_{\beta ,\omega }}}\\ \le C{\lambda }^{-1}{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|}.\end{array}$

综上，由 $J_1,J_2$ 和 $J_3$ 的估计可得

$\left|\left\{x\in R^n:\left|{\mu }_{\Omega ,b}f\left(x\right)\right|>\lambda \right\}\right|\le C{\lambda }^{-1}{\displaystyle \underset{j=-N}{\overset{N}{\sum }}\left|{\lambda }_j\right|}\le C{\lambda }^{-1}{\left({\displaystyle \underset{j=-N}{\overset{N}{\sum }}{\left|{\lambda }_j\right|}^{\frac{n}{n+\beta }}}\right)}^{\frac{n+\beta }{n}},$

再对f的所有原子分解取下确界，即可完成定理的证明。

基金项目

江西省自然科学基金(项目编号: 20192BAB201003)。

NOTES

^*通讯作者。