1. 引言
振动试验用于评定设备在其预期的运输和使用环境中的抗振能力 [1]。目前,不仅需要通过振动试验模拟复杂的振动环境,还需要通过振动筛选出早期产品工艺、组合零部件和元器件的缺陷。如振动试验可以发现产品设计、工艺、制造、装配中的缺陷,充分掌握产品的响应特性和薄弱环节。因此,振动试验被越来越普遍地采用,同时也发挥着越来越重要的作用。
进行振动试验,离不开振动夹具。振动夹具设计是振动试验中一个重要的环节,关系到试验的成败、试验结果的可信程度等 [2]。早期由于对试验夹具重要性认识不够,通常凭经验甚至感觉来设计夹具,设计的主要目的也只是简单的满足安全使用和模拟安装结构。基本上以刚性设计为主。由于没有正确的方法指导,造成了不必要材料的浪费,同时,由于缺乏必要的计算分析,也没有振动试验测试,结果夹具传递的振动往往存在着信号失真,误差很大,造成试验件的浪费和试验不真实。随着对夹具的重视,人们开始对夹具有了深入的研究。邹文俊等 [3] 对高精密夹具进行模态分析,并进行优化设计,避免了与机床加工频率产生共振。杨忍民 [4] 通过建立振动台、夹具和试验件的力学模型,探索了夹具设计的基本原则。姜同敏 [5] 经过工程实践经验总结了夹具设计和动态测试技术;刘继承等 [6] 利用Ansys对某机载雷达天线振动试验夹具进行了动态特性分析,成功的设计出满足设计要求的夹具。王柯等 [7] 对振动夹具的动力学设计提出了拓扑优化方法。闫勇等 [8] 对光学小卫星振动夹具设计及动态特性进行了分析。
本文采用有限元法(Finite element method, FEM)对某型无人机油箱振动试验夹具进行模态分析 [9],获得油箱夹具的固有频率和振型,分析其前三阶固有频率和振型,并通过扫频试验进行验证,说明夹具对后续油箱试验不会产生影响,保证了试验的真实可靠,并为试验中测试传感器的布置提供了依据 [10]。本文建立了一套油箱振动试验夹具的动响应分析方法,为振动试验夹具设计提供了方法和思路,具有一定的工程应用价值和借鉴意义。
2. 夹具的有限元模态分析
2.1. 模态分析理论
任何结构或部件都有其固有频率和相应的模态振型 [11] [12],这些属于结构本身的固有属性。模态分析实质是计算结构振动方程的特征值和特征矢量。其结构动力学运动微分方程为:
(1)
式(1)中M,C,K分别为质量矩阵,刚度矩阵和阻尼矩阵,
分别为结构的加速度矢量,速度矢量和位移矢量;
为结构的激振力矢量。
当结构不受外力、不计阻尼时,系统运动微分方程为:
(2)
假设其解为:
带入式(2)中特征方程为:
(3)
通过对式(3)求解可以得到结构的振动系统的固有频率、振型。
2.2. 夹具有限元模型的建立
对于夹具有限元模型,因其结构较为复杂,选用四面体单元,为了保证求解的精度要求,选用十节点的四面体单元。夹具选用结构钢(Q235),其材料特性参数:弹性模量2E+11Pa,泊松比为0.3,密度为7850 kg/m3。建立油箱振动夹具有限元模型如图1所示,右下角是夹具底部螺栓孔放大图。有限元模型模拟了夹具各零件和施加了附属部件的质量。
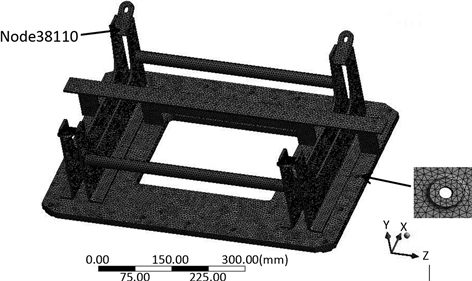
Figure 1. Finite element model of fixture
图1. 夹具的有限元模型
2.3. 夹具模态有限元结果分析
为了保证计算分析的准确性,采用MSC.Patran/Nastran及Ansys两款软件对振动夹具进行模态分析,其约束方式与实际试验中夹具的安装状态一致,在夹具底面所有螺栓孔约束X、Z方向,底面凸台面约束Y方向。计算得到振动夹具的固有频率如表1,其振型图如图2所示。
从表1中可以看出,对于振动夹具,采用两款软件求解的固有频率结果相差很小,差值最大在2.9 Hz,说明两种软件进行模态分析均能得到较为真实的计算结果。从图2中第一阶振型图可以获得,振动夹具

Table 1. Natural frequency of vibration fixture
表1. 振动夹具的固有频率
振型最大处发生在夹具的两个角上,且在Z轴方向变形量最大,Patran中整体变形量最大为31.7 mm,Ansys整体变形量最大为31.736 mm,两款软件整体变形量基本一致;第二阶振型图其振型最大处发生在振动夹具第一阶振型对面的两个角上,也是在Z轴方向变形量最大,整体变形量基本一致;振动夹具的第三阶整体变形最大处发生在连接夹具两角的钢管中心位置,弯曲变形量最大,Patran整体变形量最大为48.2 mm,而Ansys整体变形量最大为47.752 mm,整体变形量基本一致。两款软件的振型图基本一致,验证了仿真计算结果的准确性。这种数值仿真的结果为之后的振动夹具扫频试验,提供了有利的参考依据,同时也为传感器的布置提供有利的选择依据。
3. 夹具频响应有限元仿真分析
在频响应分析中,MSC.Patran有两种不同的数值方法:直接法和模态法,直接法适用于小模型,网格规整单元求解,模态法适用于大模型,由于选用油箱模型较大,单元数量多,本文采用模态法对油箱进行频响应分析 [13],在夹具Z轴方向底部施加单位力1 N,频率范围10~500 Hz,可以得到如图3所示的频响应函数曲线图。其节点38,110选取因根据振动夹具模态分析的结果,选取振型最大处位置的点,此为振动夹具其中一个角上的节点,如图1夹具的左上角所示。
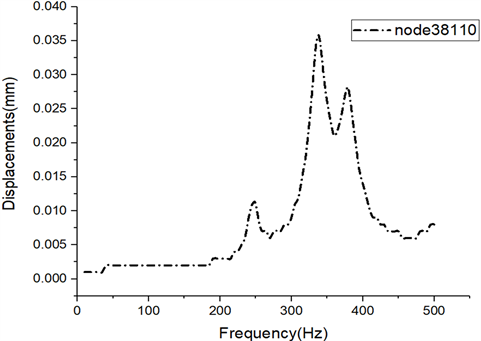
Figure 3. Frequency response curve of fixture
图3. 夹具的频响应曲线图
从图3可以看出,振动夹具在248 Hz处出现了位移峰值,说明此时的频率是夹具的共振频率。
4. 夹具的正弦扫频试验
4.1. 扫频试验装置
正弦扫频是最普遍的激振方法 [14],它是借助激振设备对被测对象施加一个频率可控的简谐激振力 [15]。这一扫频方式在扫描频带范围内,扫频信号将具有连续频谱,能激起该频带的所有振动模态。在低频去设置位移为目标值,高频去设置加速度为目标值。根据振动环境试验的标准和油箱振动试验的频率范围,扫描频带为10~300 Hz,采用恒加速度1 g进行扫频,本次扫频试验装置如图4a所示,其基本原理示意图如图4b所示,试验分析系统由功率放大器、电动振动台体、垂直附加台面、风机、振动控制仪。
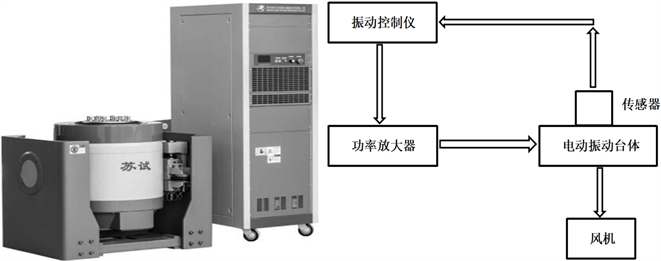 (a) 扫频试验装置图 (b) 扫频试验原理示意图
(a) 扫频试验装置图 (b) 扫频试验原理示意图
Figure 4. Sweep frequency test device and schematic diagram
图4. 扫频试验装置及原理图
4.2. 传感器的连接与布置
试验采用加速度传感器 [16],在振动夹具上布置四个传感器,一个布置在振动夹具的台面上如图5中的控制点,另外三个传感器的布置因根据数值仿真的结果,布置在其振型最大处附近,振动夹具的两个角上如图5中的监测点。传感器的布置位置如图5所示。
4.3. 试验结果
通过四个传感器,其中一个是控制点,另外三个传感器是监测点,得到夹具各个传感器的扫频曲线图如图6所示。
从振动夹具的扫频结果可以看出,四个传感器测出的曲线图都在253 Hz处存在加速度峰值,说明此时的频率是振动夹具的共振频率。图6中在峰值前段也存在小的加速度峰值,可能是夹具的毛刺,加速度传感器存在一定的质量造成的,可以忽略其影响。综合之前数值仿真结果振动夹具频响应,夹具在248 Hz时存在位移峰值,和扫频结果对比,误差在2.65%,满足工程应用误差10%的要求。油箱振动试验夹具第一阶固有频率(共振频率)为253 Hz是油箱第一阶固有频率为28.29 Hz的8.94倍,其远大于4倍的试验件要求,这一结果将为后续的油箱试验提供了有效性的保证。
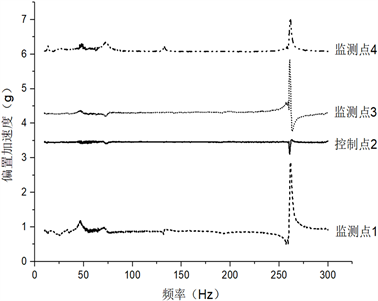
Figure 6. Sweep curve of four sensors
图6. 四个传感器扫频曲线图
5. 结论
本文利用有限元软件对某型无人机的油箱振动试验夹具进行了仿真模态分析和频响应分析,并结合扫频试验结果进行了验证,确定了计算分析的准确性。分析总结如下:
1) 从振动夹具振型云图可以看出其前两阶最大振型为弯曲和扭转组合变形,发生在夹具上部四个角上,Z轴方向变形较大;第三阶振型为弯曲变形,发生在连接夹具两个角的钢管上,Y轴方向变形较大。
2) 利用了MSC.Patran和Ansys两款软件进行模态分析,振动夹具固有频率差值1.11~2.9 Hz,最大差值为2.9 Hz,说明两种软件进行模态分析均能得到较为真实的计算结果。
3) 根据振动夹具频响应仿真曲线图,可以看出其在248 Hz处存在位移峰值,说明此时是夹具的共振频率。从振动夹具的扫频试验结果,可以得出其在253 Hz处存在加速度峰值,对比有限元仿真的结果和试验结果,误差为2.65%,试验结果验证了有限元计算仿真的准确性。
4) 振动夹具第一阶固有频率(共振频率)为253 Hz是油箱第一阶固有频率为28.29 Hz的8.94倍,其远大于4倍的试验件要求,这一结果说明了振动夹具满足后续油箱振动试验的技术要求,在油箱振动试验频率下试验夹具不会发生共振,夹具传递的振动均匀,横向振动小的特点。
基金项目
横向课题:9L3-10燃油系统研发。