1. 引言
最优投资组合的理论和算法是数理金融学中的一个重要问题,从马科维茨(H. Markowitz) [1] 提出的投资组合理论至今已有半个多世纪,然而关于最优投资组合的研究依然方兴未艾,众多学者从多方面、多层次地推广了马科维茨的模型 [2] [3],近年来,叶中行 [4] [5] 等研究了一般市场条件下投资组合的增长率以及log-最优投资组合的极限定理。本文在此基础上利用渐近样本相对熵 [6],研究了更一般的情况下序列投资组合的极限定理。
假设市场上有m种股票可供投资,投资者的初始财富为单位资金,他每次都将经上期末所得财富全部投资于下一个周期.在第n个周期中,m种股票的收益向量为
,其中
为第n个周期第j种股票的收益。在第n个周期中,投资者采取的投资组合向量为
,其中
表示在第
n个周期中分配在第j种股票上的资金比例,满足
,
,表示不允许卖空那么,
投资者在第n个周期末的累积资金为
(1.1)
累积收益率为
,其中
。
设收益向量序列
的联合概率函数为
,其边缘概率函数为
。为了刻画其联合分布与其边缘乘积分布之间的差异,受文献 [7] 的启发,我们引入:
定义1 设
为一列单调不减的实数列
,定义似然比:
(1.2)
称
(1.3)
为渐近样本相对熵。
定义2 设函数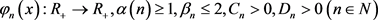 为常数,且满足当
时,有
为常数,且满足当
时,有
(1.4)
引理1 设
为一列似然函数且满足
(
是常数),
为一列单调不减的实数列,且满足对任意的
,
(1.5)
则
几乎处处收敛,且
(1.6)
证明因为
是似然函数,易知
是鞅,其中
是自然
代数流。注意到
,由鞅收敛定理知:
几乎处处收敛。又,对
由切比雪夫不等式有
由Borel-Cantelli引理可得(1.6)成立。
2. 主要结论及证明
定理 设
为连续投资于m种股票的收益向量序列,
为投资组合向量序列,设
是一列正的实数列,且满足(1.5)。令
(2.1)
如果
(2.2)
其中
,则
(2.3)
证明:令
(2.4)
其中
为示性函数。
当
,有
(2.5)
于是
(2.6)
由Borel-Cantelli引理
(2.7)
所以
收敛a.s. (2.8)
因为
(2.9)
所以
(2.10)
令
,易知
。定义
(2.11)
易知
是概率密度函数。定义随机变量如下:
(2.12)
易知
,则由引理1有
(2.13)
由不等式
,并注意到
,有
(2.14)
又
(2.15)
由(2.2)和(2.14),(2.15)有
(2.16)
从而
(2.17)
由(2.13)和(2.17)有
(2.18)
分别令
有
(2.19)
(2.20)
于是
(2.21)
由 (2.8),(2.10)和(2.21),得
(2.22)
由Kronecker引理知
(2.23)
即
。
基金项目
安徽工业大学大学生创新创业项目:信息论与最优投资组合理论的若干问题(s201910360389)。